Станислав Янков
Потребител-
Брой отговори
2763 -
Регистрация
-
Последен вход
-
Days Won
1
Станислав Янков last won the day on Септември 20 2024
Станислав Янков има най-харесвано съдържание!
Всичко за Станислав Янков

- Рожден ден 23.06.1976
Лична информация
-
Пол
Мъж
-
Пребиваване
Кюстендил
Последни посетители
Станислав Янков's Achievements
-
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
Няма да го направя - все някъде трябва да се сложи край на заниманията с коментиращия, затова ще си останеш само с благодарността за намерените от теб линкове. Не държа да ми се извиняваш, достатъчно ми е коментарите да се занимават с коментираното, вместо с коментиращия. -
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
Благодаря, Гравити - ще ги видя по-внимателно довечера (след работа). -
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
Има инертна и гравитационна маса (равни помежду си), за които може да се каже, че не играят роля при безтегловност (изключва ролята на гравитационната маса) и движение по инерция, без сблъсъци (изключва ролята на инерната маса). Дори и при това положение - аз не виждам смисъл да се каже, че масата в покой губи смисъла си. Това е все едно да се каже, че собственото време губи смисъла си, понеже е инвариантно (не зависи от отправната система). И всичкото това е всичко друго, само не и елементарно! -
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
Логиката изглежда елементарна, но дали е и утвърдената, след като малко по-рано Гравити написа, че логиката към масата да не се прилага лоренцова трансформация (макар Фейнман да я прилага) било въпрос на конвенция и по-удобно да не се прави, макар да не било непременно невярно. Можеш ли да покажеш повече или по-малко сериозно място, където масата да се определя точно по цитираните от теб начини, защото точно ти и Скенер показахте сериозни места, където прилагането на лоренцова трансформация към масата се отхвърля. Аз досега не съм срещал споменатото от теб интерпретиране на масата (не толкова, че може да се определи като инвариантна, колкото - че губи смисъла си и че може да е "собствена маса") и моля да простиш елементарното ми невежество и подозрението ми към елементарните логики по отношение на СТО, но предпочитам да го видя и някъде другаде, освен в твой коментар, особено пък и когато може да има конвенции, където масата не е инвариантна... Аз не смятам, че съществува ситуация, в която масата в покой да губи смисъла си, макар в безтегловност в Космоса и при инерционно движение/покой (когато липсват сблъсъци с други масивни обекти) да не може да се отчита. На това ти отговорих и не мисля, че отговорът ми е толкова лишен от смисъл, колкото ти и Гравити го представяте. -
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
Не е, защото самата днешна наука признава, че настоящата теоретична база не е окончателната теория на всичко. Теориите на относителността и квантовата механика в момента са като нютоновата механика - знае се, че трябва да има нещо още по-добро от тях, само все още не се знае какво е то (днес не е като преди експеримента Майкелсън-Морли, когато най-искрено са смятали, че са открили всичко най-важно и трябва само да се преодолеят последни едно-две препятствия, за да си дойде всичко на мястото). След като е потвърдено, че теориите на относителността и квантовата механика не са окончателната теория (такава може да не бъде открита никога, дори и да бъде открито нещо по-добро от тях), значи те са догми, които са следвани изключително упорито, само защото са по-добри от всичко предишно, а още по-доброто от тях, за което се знае, че трябва да го има, все още не е открито. Не може самата наука най-официално да твърди, че настоящата теоретична база не е окончателната, но аз да хуля тази база и даже чак и науката като цяло, когато твърдя същото (с израза "догма" твърдя това - отношение към нещо като да е последна инстанция, без то да е такава всъщност)! Не мога да разбера, защо тука постоянно се води някаква война и преследване, сякаш е поругана честта на девственица и виновника едва ли не трябва да бъде убит с камъни?! Толкова ли не може да се води уважителна към другите дискусия, с уважаване на тяхното право да не знаят разни неща и да се оказва добронамерена помощ, вместо постоянно да се натъртва на техни лични слабости и недостици, дори когато те си ги признават?! Задължително ли е отношението да е такова, все едно съм обезчестил горката наука и за наказание постоянно да ми се повтаря, колко малко зная, колко съм неук и мързелив, как не съм изучил за няколко години "елементарни" неща, за които над 90 процента от човечеството на планетата дори няма да чуе, камо ли пък да ги разбере, през целия си живот и куп други подобни съвсем излишни личностни квалификации и оценки (това, че понякога са завоалирани, не променя същността на намеците)?! Повтаряйте колкото искате, колко глупаво е нещо, друго или трето, написано от мен, като не пропускате да споменете, защо го считате за чак толкова глупаво, но защо е нужно да се включват и оценки за мен самия?! Или щом това е нормално - аз също мога да напиша, колко тъпо постъпваш ти, Гравити, като се държиш с други рязко и високопарно, пък не си си направил труда да овладееш нещо толкова същностно като разслоенията и как те могат да се прилагат във физиката? Трябва ли и аз да започна да отвръщам на всяка квалификация по мой адрес със същото към отсрещната страна и на какво ще заприлича тогава разговора?! Мога и да отговоря на какво ще заприлича - на "разговорите" с Младенов, Джереми и други по едно време... Ето цяла дузина коментари, които нямат нищо общо с коментиране на физика, от които няма почти никаква или никаква полза (поне за мен няма) и заради което ще си направя една добра-а-а-а, продължителна ваканцийка... Успехи! -
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
В продължение на години главно ти и Скенер упорито се борите срещу всяко споменаване на диаграмите на Епщайн и Евклидовата относителност, за да признаеш ти в един момент, че диаграмите не са напълно неверни (няма и как, след като произхождат от конусите на Минковски), а Скенер, че има неща, които те представят точно (съвпадат с резултатите от лоренцовите трансформации и диаграмите на Минковски), макар да имат и слабости (и диаграмата на Минковски не може да представи едновременно всичките четири измерения - трите пространствени и времевото). И след това - отново пълно отричане и охулването ми. Отговарях на всичко това, вместо просто да го игнорирам и да продължа с други твърдения (например - че масата в покой се дължи на движение на материята в четвърто или даже пето измерение), понеже се стремях да отговоря на критиките и да коригирам детайлите, относно които бяха забележките. Очакването да отрека всякаква възможност пространство-времето да се представи единствено чрез пространствени измерения, но повече от три, без да е изчерпан всеки опит в тази посока и да започна най-стриктно да рецитирам само пространствено-времевия подход и неговите интерпретации, за да не изглеждам арогантен и надменен, не отговаря на моя характер и ако аз и това ми поведение сме най-големия проблем на този форум - мога да го разреша НЕЗАБАВНО! И за всичко се използват САМО теориите на относителността (кръгова логика), като едва ли не съвършен конспект без никви слабости, а ТО дори не могат самостоятелно, без квантовата механика, да се приложат към микроскопичния свят! Едновременно, СТО се съчетава изключително сложно и нехармонично с квантовата механика до квантовата теория на полето (налагат се пренормировки), а пък ОТО в частта си за гравитавитацията въобще не може да се съчетае с квантовата механика. В същото време квантовата механика сама по себе си е неприложима към макросвета... И при всичко това се разправя, как дадени разсъждения били излишни допълнителни пластове, които трябвало да се режат с "бръснача на Окам", били излишни косми и т.н. На мен ето това ми се струва арогантно и надменно, но нито веднъж не съм си позволил да отправя подобен упрек към теб и Скенер. Ти обаче си решил, че към мене може! Може би защото вече си обединил успешно ОТО и квантовата механика и скоро ще го обявиш... Не разбираш достатъчно задълбочено въпроса с разслоенията, но по презумпция допускаш, че имам някакви грешки (нещо напълно вероятно) и отказваш да посочиш някоя конкретна грешка. Само ме охулваш, че не съм учил с години определени неща и затова не искаш да посочиш нещо конкретно! Разбирам, че според вас коментаторския ви подход е идеален и напълно обоснован, а такива арогантни и надменни като мен не може да пишат тук, без да знаят всичко. Нямам право да не зная разни неща, но упорито да застъпвам някаква концепция, която не съвпада с догмата за момента. Аз, обаче, съм на друго мнение и по този въпрос! Успехи! -
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
Шпага, аз колко пъти съм ти написал, че не разбираш дадена материя, не си учила достатъчно, не знаеш елементарни неща и целия ми коминтар към теб да се изчерпва само с това, без нищо по същество (виж онзи твой коментар, че щом не сме се разбирали за неклщо толкова "елементарно"...). Покажи ми поне един такъв мой коментар към теб! Една дума не си сложила като обяснение за онези неща за масата, които си видяла, че не разбирам! Наистина ли болшинството тук не умеете да коментирате по същество, без да се занимавате със слабостите на даден коментатор като квалификации по негов адрес?! Аз съм си позволявал подобни неща по адрес на Младенов, преди да започне да цитира разни добри материали, но това беше, понеже дотогава ВСЕКИ негов коментар включваше подобни оценки за опонентите му (от сорта - колко глупави били научниците и други подобни). -
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
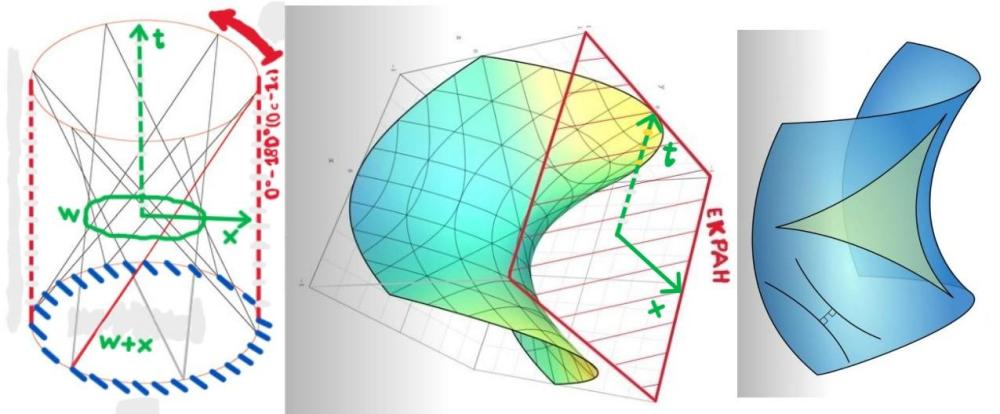
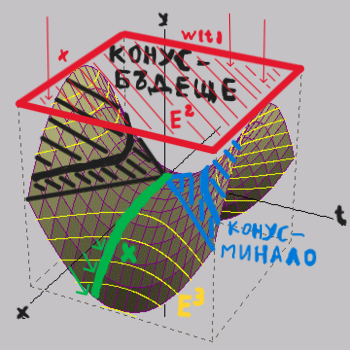
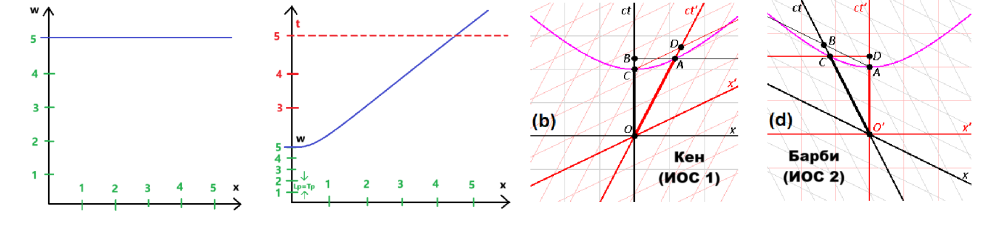
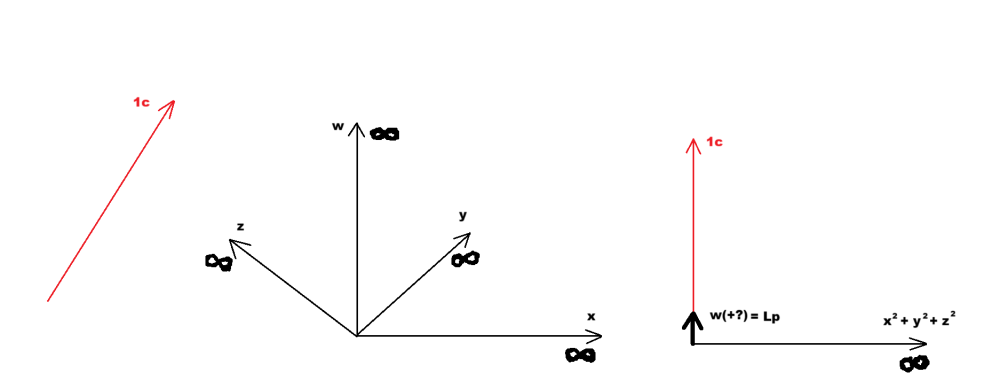
Там има доста повече. Това е по-общ (не особено детайлен, иначе книгата можеше да надхвърли и 10 000 страници) справочник на всички неща във физиката, които Пенроуз счита по-значими. И особено собствената концепция на Пенроуз за светлината като би-туисторна конфигурация (с всичките там туисторни пространства и пространство-времена на Минковски, които се ползват за излагането на тази концепция). Подходът на Пенроуз, заедно с разслоението на Клифърд, ако някога бъдат разбрани по-добре от мен, ще ми помогнат много за развитието на собствената ми концепция. За последен път ще опиша накратко нейната аналогична на Специалната теория на относителността най-най-обща и предварителна форма и ще престана да цикля непрекъснато на едно и също място, защото отдавна е крайно време да опитам да формирам нещо подобно и относно гравитацията и квантовата механика (поне някакъв много начален градеж, който след това да се развива и усъвършенства чрез включването на все повече детайли от СТО, ОТО и квантовата механика). Ако степените на свобода си остават само три транслационни (плюс свързаните с тях три ротационни), пространствените измерения биха могли да бъдат повече от три. При съкращаване на пространственото отстояние на Вселената по направлението на четвъртото пространствено измерение w, докато пространственото отстояние по направлението на останалите три пространствени измерения (например – по посоката на движение в 3D-пространството xyz) се удължава със същата стойност или обратното (тоест – при увеличаване и намаляване на скоростта между обекти в 3D-пространсството xyz), степените на свобода (транслационните) биха могли да си останат три през цялото време, докато пространствените измерения могат да бъдат четири или дори повече. Важното е степените на свобода (транслационните) да остават през цялото време средно три пълноценни. Дефинираме съответствие между концепцията на фундаменталния покой (Блоковата Вселена) и концепцията на фундаменталното движение (Динамичната Вселена или хиперизмерния базис с абсолютно хиперизмерно движение). Съответствие – всеки елемент на едната част от съответствието (едната от двете концепции) трябва да притежава някакво представление, даже и на пръв поглед съвсем несвързано или пък огледално-противоположно, в другата част на съответствието (другата от двете концепции). Имаме векторът (стрелка) на хиперизмерната (четиримерна пространствено) скорост 1с, който сочи само в една, конкретна посока и води до лоренцово съкращаване на дължината в тази посока (всичко това са „вътрешни“, инвариантни особености). Това е векторът на константното, абсолютно хиперизмерно движение с темп 1с на вселенската материя спрямо всичко, което не се движи почти изцяло по направлението на четвъртото пространствено измерение w (на четвъртата пространствена координата w). Нека произволно да изберем този вектор да сочи почти вертикално нагоре. Това е тензор, инвариант (тоест – той е абсолютен). Спрямо него, бидейки той „вътрешен вектор“, се върти също „вътрешна“ четиримерна (хиперизмерна) декартова координатна система (четиримерно плоско, евклидово пространство). Преди да бъде съединена с вектора на хиперизмерната скорост 1с, базисните вектори на четиримерната декартова координатна система са с безкрайна дължина. Това „вътрешно“ евклидово пространство (декартова координатна система) може да бъде завъртано около „вътрешния“ вектор на хиперизмерната скорост 1с по два различни начина - или по евклидов кръг, подобно на диаграмите на Епщайн, или да се ползва лоренцовата формула при затъртането на координатната система (тогава скоростта по направлението на координатата w намалява под 1с, скоростта по направлението на координатата х се увеличава над 0 и чрез лоренцовата формула се определя увеличаването на дължината по w над 0 и съкращаването на дължината по х под безкрайност). Диаграмно, като пространство-време, тази комбинация между вектора на хиперскоростта и хиперпространството се представя чрез „деформирано“ като „седло“ „вътрешно пространство“, наблюдавано през „евклидовия екран“ на пространствено-времевата диаграма на Минковски. Така се стига до хиперболичната права, която може да се определи и като квадрант на хиперболична окръжност, която е свързана с въртенето на примовите координатни системи при диаграмите на Минковски. Горното представяне беше условно, само като илюстрация на правилния начин на описание на прехода от хиперизмерна (четиримерна) декартова координатна система към пространствено-времевата диаграма на Минковски (изкуствения подход с ротацията на Вик е прекалено елементарен и поради това практически не работи). Всичко това обаче има и реална физическа аргументация. Ние се помещаваме в пространството, но не се движим спрямо пространството (няма как да се движим спрямо нещо празно), движим се (или сме неподвижни) спрямо други материални обекти в пространството. Материята, със своя вектор на хиперизмерната скорост 1с, се движи в хиперизмерно (четири-пространствено) евклидово пространство (декартова координатна система с четири ортогонални един на друг лъча с безкрайна протяжност) и води до лоренцовото съкращение на пространството по направлението на своята посока. Но това не значи, че тази материя се движи спрямо споменатото пространство, в което вектора с темп 1с е разположен по някакво направление. Всеки обект в инерциално състояние счита себе си покоящ – инвариантно, абсолютно състояние според всеки материален обект. Това означава, че за всеки обект инерционното му състояние се изразява в насоченост на вектора на хиперизмерната скорост 1с на обекта почти напълно по направлението на четвъртото пространствено измерение w. Така покоящ обект се движи по инерция (без да усеща подобно движение – ходът на времето не се усеща, а се предполага чрез опита) почти напълно по направлението (по координатата) на четвъртото пространствено измерение w и това съкращава пространството на този обект по това четвърто направление до планковата дължина. Понеже всички считаме себе си в покой, равностойно може да се каже, че останалата част от вселенската материя се движи спрямо нас по направлението (по координатата) на четвъртото пространствено измерение w и затова нямаме достъп до това измерение, като за нас това е инвариантно, абсолютно състояние (постоянна особеност на собствената координатна система). Спрямо какво по-точно се движим с хиперизмерната скорост 1с почти напълно по направлението на координатата w (какво по-точно се движи спрямо нас с хиперизмерната скорост 1с почти напълно по направлението на координатата w), след като това не е пространството? Хиперизмерно движение на каква точно материя представлява този вектор (хиперизмерна светлина?) и спрямо какво точно се движи? Светлината се движи изцяло в 3D-пространството хуz и не разполага с времева компонента, тоест – няма дял от движението си по направлението на четвъртото пространствено измерение w. Няма нещо, по отношение на което светлината да не се движи със скоростта на светлината. Това значи, че светлината се движи изцяло в 3D-пространството хуz спрямо всички материални обекти, които не се движат изцяло в 3D-пространството хуz, ами имат и времева компонента (тоест – движение и по направлението на координатата w). Ние се движим почти изцяло по направлението на четвъртото пространствено измерение w спрямо всичко, което не се движи почти изцяло по това направление (движим се по това направление спрямо всичко, което не е в 3D-покой спрямо нас). Всичко, което се движи почти изцяло по направлението на четвъртото пространствено измерение w (на четвъртата пространствена координата w) е неподвижно спрямо нас в 3D-пространството хуz, без да може да заема същото пространствено местоположение като нас (материята с изцяло 3D-движение, като светлината, може да заема едно и също място в 3D-пространството – макроскопична суперпозиция). Относно възможността за представяне на Блоковата Вселена като базис на разслоение - ето какво отговори изкуствения интелект на Гугъл: "Блоковата Вселена, където миналото, настоящето и бъдещето съществуват вечно, може да бъде концептуализирана като Разслоение като разглеждаме пространство-времето като геометрична структура, където срезовете (като пространствени хиперповърхности, представляващи "моменти") са "слоеве" над "базово пространство", често свързани с теории на квантовата гравитация или унифицирани полеви теории, използващи топологични структури като Хопфова фибрация (S¹ → S⁹ →CP⁴). В тази гледна точка Блоковата Вселена (4D многообразие на пространство-времето) е "разрязана" на тези моментни слоеве, като геометрията на разслоението описва как тези срезове (и квантови състояния върху тях) се свързват, свързвайки статичната блокова гледна точка с динамиката и квантовите явления чрез топологични обрати, където слоят (като U(1) фаза) представлява физични степени на свобода като електромагнетизъм или Стрелата на времето. Блоковата Вселена и пространствено-времевата фолиация Блокова Вселена (Вечност): 4D пространствено-времеви блок, където всички събития (минало, настояще, бъдеще) са еднакво реални, последица от теорията на относителността. Пространствено-времева фолиация: Начин да се разреже този 4D блок на 3D "срезове", представящи различни "моменти" или пространствени хиперповърхности, като кадри на филм. Проблемът: Стандартната квантова механика изглежда дава предимство на едно единствено "сега" (колапс на вълновата функция), което противоречи на времевата симетрия на блоковата вселена. Разслоение като решение Топологични полеви теории: Изследователите използват математически разслоения (като разслоението на Хопф), за да моделират пространство-времето, където 4D блоковата вселена е вградена в пространство с по-високи измерения. Слоеве (моменти): 1D влакно (например кръг S¹) в разслоението може да представлява специфичен "момент" или квантова фаза (U(1) симетрия), докато базовото пространство (напр. CP⁴) съдържа динамиката. Динамика и време: "Усукването" на слоевете над базовото пространство описва физически взаимодействия (като електромагнетизъм) и възникването на времето, което позволява на иначе статичен блок да прояви промяна и квантово поведение. Връзка "Растящ блок": Този подход към разслоението може да помогне за примиряване на Растящия блок изглед (където блокът "расте" с нови моменти) с основната статична блокова структура, като се интерпретира динамиката (растежът) като произтичаща от свойствата на слоя. По същество разслоението предоставя математическа рамка за "разгръщане" на статичната блокова вселена в динамична, квантова реалност, като третира времето и физическите взаимодействия като топологични характеристики на геометрия с по-високи измерения, превръщайки илюзията за преминаване на времето във възникващо свойство на тази комплексна структура. Концепцията за Блокова вселена, където минало, настояще и бъдещи събития съжителстват в статичен 4D пространствено-времеви "блок", е основна интерпретация на теорията на относителността и я разглежда като Разслоение предлага математическа рамка за разбиране как динамиката (като потока на времето или калибровъчните полета) може да произлезе от тази статична геометрия, особено в теории като Топологична обединена теория на полето (TUFT), където слой (като окръжност) представлява вътрешни фази (свобода на време/калибровъч), усукани над базово пространство (пространство-време), позволявайки възникваща промяна и причинност. По същество фибрационният модел предполага, че нашият опит за преминаването на времето не е фундаментален, а възниква от взаимодействието между статичния блок (базата) и тези вътрешни степени на свобода (слой). Обяснение на Блоковата вселена Вечност: Блоковата вселена, или вечността, твърди, че всички моменти във времето са еднакво реални, като кадри във филмова лента, а не като течащ настоящ момент. Пространство-време: Теорията на относителността слива пространството и времето в едно 4D многообразие, блока пространство-време, където събитията са фиксирани точки. Адинамизъм: Блоковият изглед предполага статична реалност; Нищо не "се случва" в самия блок, а по-скоро различни "срезове" от пространство-времето представляват различни моменти. Фибрация като модел Фибрация на Хопф: Теории като TUFT използват фибрацията на Хопф (S¹ → S⁹ →CP⁴), където базовото пространство (CP⁴) е пространство-времето, а влакното (S¹) представлява вътрешни степени на свобода, включително U(1) фазата на електромагнетизма и, което е ключово, стрелата на времето. Възникваща динамика: Усукването на слоя над основата позволява появата на динамика (калибровъчни полета, причинност, времеви поток), когато се наблюдава от конкретна перспектива ("сечение" на фибрацията). Квантувано време: Периодичната природа на слоя може да генерира квантувани фазови измествания, свързвайки го с наблюдаеми явления и структурата на времето. Свързване на концепциите Вместо времето да бъде вътрешен поток (като в модел на растящ блок), подход като разслоение предполага, че нашето възприятие за време и промяна (динамика) е следствие от начина, по който "разгъваме" или наблюдаваме различни "срезове" на статичния, безвременен блок пространство-време, като слоя осигурява механизма за тази видима еволюция. Тази математическа структура позволява на физиците да примирят статичната природа на блоковата вселена с динамичния, променящ се свят, който преживяваме, като поставя "стрелата на времето" в топологията на пространство-времето, а не във фундаменталния поток. В съвременната физика и космология към 2026 г., Блоковата Вселена (етернализъм) все повече се анализира през математическата призма на Разслоения, за да преодолее пропастта между статичното четириизмерно пространство-време и динамичния опит на времето и квантовите явления. Блокова вселена като разслоение Разслоението е математическа структура, при която "тоталното пространство" (блоковата вселена) се проектира върху "базово пространство". Това позволява няколко напреднали интерпретации: Пространствено-времева фолиация: 4D блоковата вселена се разглежда като глобално хиперболично многообразие което може да бъде "разрязано" или фолирано в 3D пространствени хиперповърхности. В термини на разслоението, всяко парче (слой) представлява състояние "сега", а базовото пространство представлява прогресията на времето. 5D разклоняващи се многообразия: Последните изследвания от 2025 г. предлагат 5D разслоение за да съгласуват блоковата вселена с квантовата механика. В този модел 5D многообразието (общото пространство) съдържа "Еверетово разклоняване" (паралелни времеви линии), където слоевете са самите 4D блокови вселени. Това помага да се обясни как "сега" може да бъде перспектива, локализирана от наблюдателя в рамките на непроменяща се глобална структура. Геометрия на наблюдателя: Разслоенията позволяват Квантови състояния с фолиационна стойност, където "колапсът на вълновата функция" не е физическа промяна на блока, а проекция на локализираната перспектива на наблюдателя върху конкретен слой на многообразието. Свързани математически рамки Разслоения на Хопф: В Топологичната обединена теория на полето (TUFT), рамките от 2025 г. използват комплексно разслоение на Хопф (S¹ → S⁹ →CP⁴), за да моделират 9-измерно пространство-време. Тук слоевете (S¹) са свързани със Стрелата на времето и причинна структура, гарантираща, че времевият ред произлиза от основната геометрия. Еволюираща Блокова Вселена: Някои физици, като Джордж Елис, защитават Еволюираща блокова вселена където пространство-времето не е фиксиран 4D обект, а такъв, който непрекъснато "расте". Това може да се моделира като разслоение, при което базовото пространство (времето) е ограничено до миналото и настоящето, като бъдещето все още не е "конструирано" като част от общото пространство. Фолиацията на пространство-времето е Математическата концепция в общата теория на относителността за разрязване на четириизмерната тъкан на пространство-времето на серия от триизмерни пространствени "срезове" или "листа", всеки от които представлява момент във времето за наблюдателите в този срез, позволявайки еволюцията на Вселената да бъде описана като последователност от пространствени моментни снимки, често използвани за решаване на уравнения и разбиране на причинността. Това е като да режеш хляб на филийки, където всяка филия е пространство, а последователността е време, предоставяйки рамка за динамика и начални задачи на стойността в гравитацията. Ключови концепции: Пространствени хиперповърхности: 3D "срезовете" се наричат пространствени хиперповърхности, което означава, че във всеки срез няма времево разделение, а само пространство. Еволюция на времето: Фолиацията предоставя начин да се проследи как тези пространствени срезове се променят и развиват от един към друг, като по същество дефинира времеви параметър. Референтни системи: Различните фолиации съответстват на различни избори на референтни системи или времево разрязване, давайки на физиците свобода да изберат най-удобния начин за описание на конкретна физическа ситуация. 3+1 Разлагане: Често срещана техника в общата теория на относителността, известна като "3+1 декомпозиция", използва фолиация за разграждане на сложните уравнения на Айнщайн в уравнения на пространствена еволюция, което е от съществено значение за симулации и разбиране на динамиката. Глобално хиперболични пространства-времена: За да може пространство-времето лесно да се фолира в непресичащи се, глобално дефинирани пространствени срезове, то трябва да бъде глобално хиперболично. Аналогия: Представете си движеща се картина (пространство-време). Фолиацията е като да правиш серия от неподвижни снимки (пространствени разрези) на определени интервали, позволяващи ти да видиш как сцената се променя кадър по кадър (времева еволюция). Значение: Фолиацията е фундаментална за: · Създаване на начални условия за симулации на черни дупки, гравитационни вълни и космология. · Разработване на последователни математически рамки за гравитацията. Изследване на алтернативни теории за гравитацията, при които изборът на фолиация може да има физическо значение." Много интересно, дали реално съществува споменатия в цитата (в червено, подчертано и с удебелен шрифт) проблем между статичността на Блоковата Вселена и квантовата механика или това е някаква измислица на ИИ?! По някое време трябва да проверя това нещо! Сега обаче трябва да си почина малко от физиката и постоянните упреци колко малко зная, че месеци плътно четене и гледане на материали с физическа насоченост, съчетано с постоянни упреци тук относно липсата на познания действа прекалено дразнещо и убива всякакво желание за занимание с физика и/или за коментиране. Чао за известно време на всички (ще видим за колко точно)! -
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
Вярно е, но ти обичаш да противоречиш напук и ти е приятно създаването на подобни "сблъсъци". Аз не отричам купищата потвърдени важни детайли във връзка с теориите на относителността. Аз отричам невъзможността за изграждане на алтернативи и според мен такава възможност се съдържа в хиперизмерността в съчетание с богатото разнообразие от проекции. Не може просто със заявление да се отрича такава прекалено широка област от възможности. Ако теориите на относителността и квантовата механика бяха безусловно верни - едните щяха да успеят да се разпрострат със собствените си концепции и към микросвета, а другата щеше да се разпростре и към макросвета и щяхме да имаме две равностойни различни концепции, два алтернативни погледа над цялата реалност, които да дават различни предимства с различните си подходи. И дори и тогава нямаше да има гаранция, че не се изпуска още нещо неизвестно (всяка особено успешна концепция има тенденцията да се затваря с времето във вид кръгова логика и това не се отнася само за физиката, нито се ограничава само до потвърдената успешност в научен план). Накратко - на тебе "сблъсъците с научниците" са ти приятни и влизаш в тях с удоволствие, а аз търся ползата и когато твърде много започна да се отклонявам от специалния ми интерес и/или твърде много започна да се дразня - спирам! Това си е съществена разлика между теб и мен. -
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
Критични: "Това не е вярно, заради това и това и това (накратко, както предпочита Гравити или детайлно, както се старае Скенер). Не "критични": "Няма да ти кажа, понеже не искаш да учиш 4-5 години точно това, което аз ти казвам, че трябва да учиш." Като има съмнения, че ще разбера нещо и няма желание за обясняване - може да се спести излишен коментар, вместо само да се пише, колко малко знам, колко години ми трябват да го науча и нищо по същество. Така определено не извличам никаква полза, а и никой друг "като мен" (и не само "като мен") не би извлякъл такава. Или пък "нещо толкова елементарно", което над 90 % от населението в страната дори не го знае, камо ли да го разбира, а от населението на планетата са и още повече (аз мисля за масата във връзка с Калуца-Клайн по различен начин от "толкова елементарното", което мнозина не го разбират добре и аз също може да съм от тях, щом не разбрах точно какво имаш предвид, а Гравити е разбрал). Това, че някой разбира нещо, не значи, че то е непременно елементарно и всички останали са длъжни да го разбират колкото него, нали? Някои може просто да не са го срещали досега, за да го знаят или и да са го срещали - не са смятали, че им трябва точно в този момент и не са му обърнали внимание. Напоследък отново започвам да се дразня все повече, разговорите по темата започват да ми стават все по-неприятни, макар да има безспорна полезност (особено от детайлните разяснения на Скенер), а многократно съм споменавал, че когато стигна до това състояние - "дръпвам шалтера"! Няма да е зле отново да си почина за известно време от физиката - пак започвам да се натоварвам излишно, а това във всички случаи е контра-продуктивно. -
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
Уредени сте, за дълго време. Можехте директно да кажете, че не искате да пишат тук "такива като мен", нямаше нужда от такива заобиколни тактики! Успехи! -
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
Ако казва това - значи е права. Но тя споменава "собствена маса" и като цяло - моето впечатление от коментара и' беше, че масата в покой е безсмислена. Маса в покой си има, формулата за енергията на Айнщайн го показва и ако е имала предвид безсмисленост на отчитането на параметъра маса в покой - така не смятам, че е права. Отговарям само на съдържателните ти коментари, които не се занимават с мен. Освен това ще се изключа за малко, да проверя едни работи. -
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
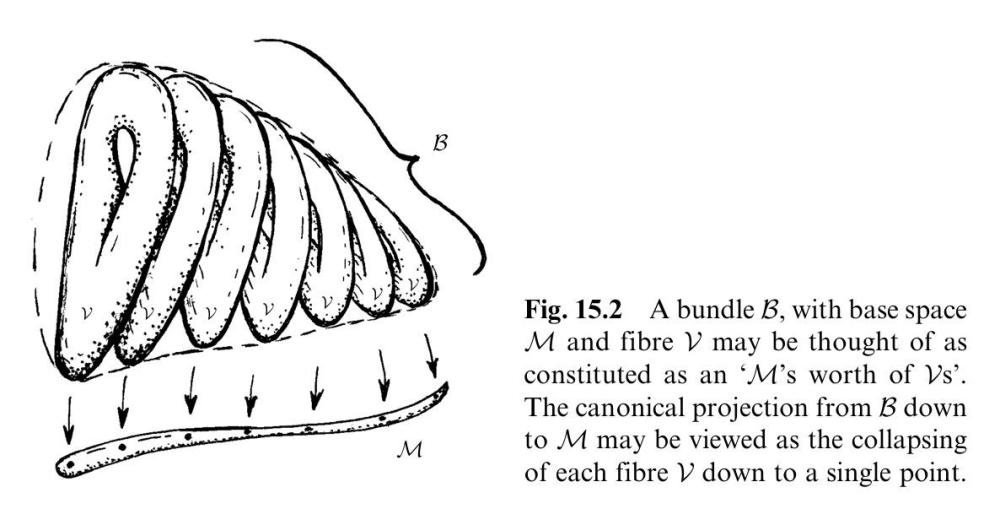
Ще ти дам нещо за основа. При Пенроуз разслоението се ползва като средство за открояване на инвариантни особености и техните компоненти. При разслоението на пространство-времето на Галилей/Нютон/Картан времето е абсолютно, инвариантно, затова се явява едномерен базис, всяка точка от който формира срез от 3D-пространственото разслоение (така е, понеже там пространството не е абсолютно като времето, а е относително - Пенроуз леко е модифицирал Нютон за целите на представянето си). При пространство-времето на Минковски/Айнщайн базисът вече е Блоковата Вселена, за чийто общ пространствено-времеви "блок" са съгласни всички наблюдатели/координатни системи, докато разслоението е комплектите от срезове (да речем - "под различни ъгли") на този общ (инвариантен, абсолютен) блок, които срезове представляват относителните параметри на компонентите, свързани с отделните наблюдатели/координатни системи. При клипа е дадена много по-общата и абстрактна рамка на всичките тези конкретни ситуации от Пенроуз - общата, абстрактна рамка на разслоенията, която може да се ползва за какво ли не, включително и далеч отвъд само физиката. Успях ли да дам адекватен отговор сравнително накратко на онова, за отговарянето на което ти ми искаш 4-5 години учене? -
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
Да и ти не си в състояние да синтезираш накратко, даже и непълно, защо клипа не е за разслоенията, какви са различните значения на fibration и fibres в клипа и при употребата им от Пенроуз в книгата му. Еми - жалко! Интересуваше ме доста, защо мнението ти е такова, без да трябва да уча 4-5 години, за да получа някакъв разбираем (достъпен за "такива като мен", както ме определи по-горе) отговор. -
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
До нищо полезно за кариерата и джоба и затова никой не ще да развие подобно направление (което да ползва само пространствени измерения, без никакви изкуствени измерения от каквото и да било друго естество, включително и времево), поне за да види, докъде би бил предела на подобно усилие, ако има такъв. За съжаление любопитните физици и математици като Картан, който е развил нютоновата гравитация до предела ѝ след успеха на Айнщайн с ОТО, явно отдавна са измрели и повече не се раждат. Наистина, по времето на Картан СТО и ОТО въобще не са представлявали това огромно, сложно и плътно взаимо-свързано нещо, което представляват днес (до степен да са кръгова логика - обясняват всички въпроси с разни други неща от самите себе си), но и такива като Картан днес си липсват...