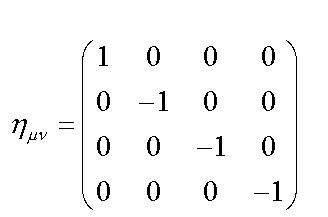Станислав Янков

Всичко е наред, наясно съм, че нищо не може да замени едно пълноценно учене на физиката цял живот, за предпочитане в реномиран западен университет с традиции във физическите изследвания. Няма как да бъде отречено, че написаното от теб е вярно (то е казваното от Гравити с доста повече подробности). За съжаление (според мен - за добро) аз не съм от фантазьорите, които ще тръгнат да си въобразяват, че тепърва ще започнат да учат пълноценно физика и за няколко години ще достигнат твоите и на Гравити знания - не само липсата на време, а и редица други ограничения не ми позволяват това. За радост - въобще и нямам такова намерение. Както по света има хора, които владеят физиката още по-задълбочено и от вас двамата с Гравити, така има и хора като мен, които знаят по-малко от вас и това ще си остане така. Макар да ми се искаше много повече - ще се оправям с това, с което разполагам в съответния момент. Не е най-приятното да комуникираш със събеседници със знания в обсъжданата област, драстично надхвърлящи твоите, докато те отделят прекалено много внимание на твоите знания или още по-точно незнания, на твоята психика (каквито твърде чести разбори беше започнал да прави по едно време Кипен, например) и да те упрекват, че нямаш възможност да направиш нещата, които по-бързо да те доближат до техните възможности, но аз съм от малцината, които са способни да оценят високо и написаното по същество, извън разборите на личността ми и на ограниченията ми. Винаги намирам начин да извлека добра полза от твоите, на Гравити и на останалите коментари, независимо кой различен от мен какво смята за това.

Например неевклидовите геометрии. Там няма и думичка за това, а е много важно. Нито има нещо за Риман, нито за Лобачевски - нищо! Пак тука от форума, от вас със Скенер, разбрах за важността на тези неевклидови геометрии (за първи път прочетох съвсем символични техни споменавания в книгите на Грийн) и с времето научих повече неща. А в книгата на Пенроуз главите за неевклидовите геометрии са едни от първите! Може би всичко е заради това, че става дума за учебници само за студенти в началото на обучението им (поне тогава, когато ги купувах, нямаше нищо друго, иначе щях да купя и останалото). Икономиксите на УНСС-то са много по-големи и пълноценни! Правя го само, защото ме интересува, а истинските физици (за разлика от мен) не щат да се захванат сериозно с това, защото е твърде сложно и твърде рисково - може да не доведе до бърза кариерна/финансова реализация. Получила се е една обхватна и разклонена, доста сложна кръгова логика, при която всякакви моменти, свързани с теориите на относителността, се разрешават единствено с практики и способи от теориите на относителността, а там, където са разработени алтернативи (квантовата механика) - те са несъвместими. Ако с това, което ме интересува в момента, се захванат истински физици и започнат да го развиват те - с най-голямо удоволствие ще изоставя темата и само ще консумирам в популярна форма плодовете на труда им. Изляза ли от рамката да ми е приятно и интересно, започне ли твърде много да ме напряга и дразни - веднага дръпвам шалтера!

Много, което не съм срещал в учебниците, но го има в книгите на Грийн, както и в тая на Пенроуз (естествено - при Пенроуз има много-много повече, отколкото при Грийн). Купища неща са, от всички области. В учебниците са дадени някои най-базови неща и още по-малко най-базови интерпретации на дадените най-базови формули. Цял куп ключови неща (и особено обяснения на резултатите от формулите) ги има разхвърляни из купища книги на известни физици ка то Уайнбърг, Фейнман и други подобни (при Пенроуз всичко това го срещам концентрирано на едно място, в една и съща книга, в най-голяма степен). Засега основният ми учебник ще си остане книгата на Пенроуз. Не съм вкъщи и не мога да проверя (от Кюстендил съм, но работя в София, пътувам за уикенда) - беше един тъмносин учебник от две части, за студенти първи курс (магистри ли се водеха там) и формулата за лоренцовата промяна на масата я имаше заедно с тези за дължината и времето, без никакви обяснения. Даже и в клиповете на eigenchris е споменато за това, а аз научих за него тук, във форума, от Шпага и Скенер. На мен ми е достатъчно, заедно с вашите корекции тук във форума, не ми трябва повече. Не пропускай, че става дума просто за хоби, не за състезание и реализация във физическата сфера - задоволяване на съвсем конкретен, специфичен мой интерес (може би произтича от нещо подсъзнателно, щом ме е заинтригувало чак толкова - знам ли!).

Аз имам учебници от Софийския университет - и за физика, и за Космология, и за квантова механика (както за Софийския, така и за Благоевградския университет). Не знам какво се преподава на лекциите, но учебните не включват дори неща от книгите на Браян Грийн, които определено не са на нивото на тая на Пенроуз. В учебниците по физика все още присъства лоренцовата промяна на масата в покой за СТО, а това отдавна е отхвърлено като невярно! Няма по-добър формат за самостоятелно учене, поне за моите цели, от настоящия, който ползвам.

Мисля да започна от това, чийто линк съм сложил (то е едно добро начало) и да потърся първоначален вариант за описание на масата чрез движение в пространствено измерение извън трите. Първоначално ще пробвам с четири, но без да е пространство-време (за да няма пето измерение, тоест - фаталната допълнителна степен на свобода). Затова и се опитвам да пресъздам времето от СТО като резултат от четвърто пространствено измерение, вместо самото време да е измерението, но още отсега усещам, че ще имам сериозни проблеми - гравитацията направо си плаче за пето измерение, пък и разни детайли около часовниковия темп в покой също дават възможност за обосноваване на повече от четири пространствени измерения. Ще бъде интересно! Ще трябва да почета още бая-бая... https://profmattstrassler.com/articles-and-posts/some-speculative-theoretical-ideas-for-the-lhc/extra-dimensions/how-to-look-for-signs-of-extra-dimensions/kaluza-klein-partners-why-step-1/

Моделът Калуца-Клайн е потвърдено провален модел, но той предлага и някои плюсове, освен минусите - чрез вграждане на 4D пространство-време в 5D рамка, геометричните уравнения на 5D гравитацията по един вид естественначин се разделят на 4D уравнения на Общата теория на относителността (GR) и уравнения на Максуел за електромагнетизъм. При по-добро разбиране на този процес (имам предвид - от моя страна) би могло да се използва във видоизменено състояние тази полезна жилка от Калуца-Клайн теорията, като се държи ясна сметка за провала на модела като цяло и за неговите слаби страни в частност.

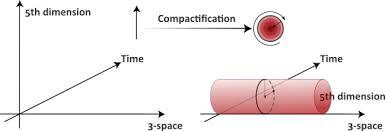
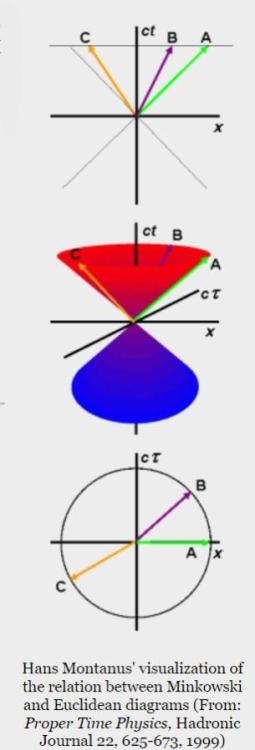
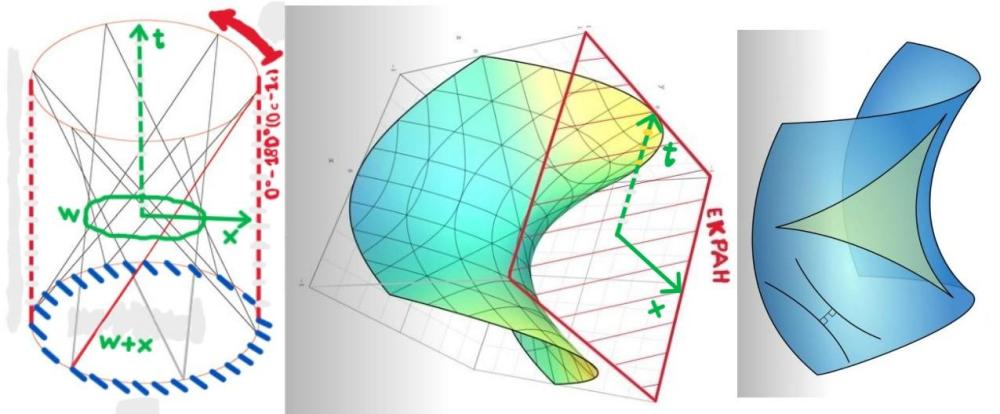
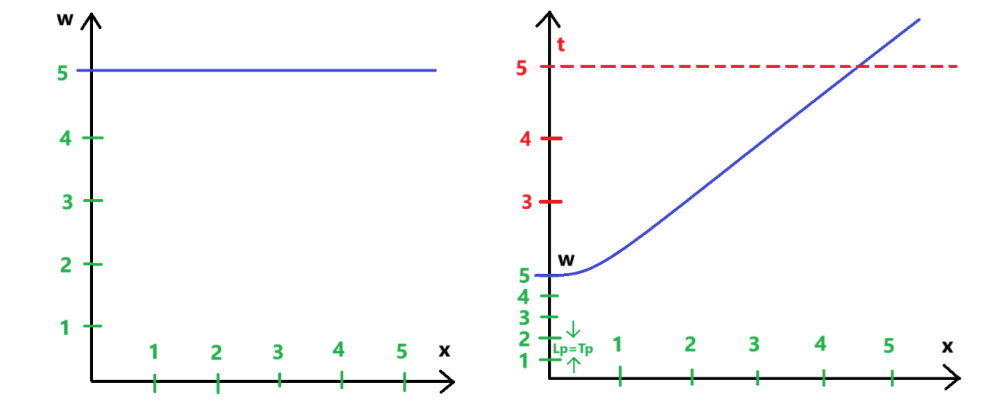
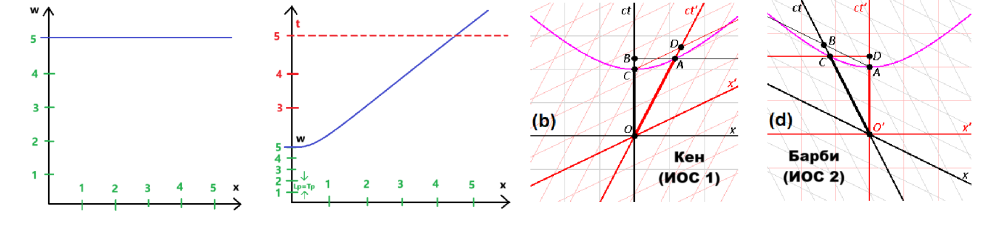
Това е квантовомеханичното описание на възникването на масата (чрез полето на Хигс). От друга страна, различните полета биха могли да се считат за различни пространства. Ако имаме едно общо многообразие (общо пространство), то да има определен брой под-многообразия (под-пространства) и това да са различните полета. Много ми е интересно, дали съществува възможност да се въведе петмерно пространство-време от типа на Калуца-Клайн, без това да води до увеличаване броя на степените на свобода, но не по изкуствения начин, по който това е направено от Калуца (при него просто се постулира правилото на цилиндъра). За визуализация на петмерно пространство-време на Калуца-Клайн отлична работа би свършила една диаграма от Монтанус, направена с други цели, само там ще се промени названието на координатата, именована от Монтанус сТау на координата w. Често използваното изображение относно Калуца-Клайн е това:

Не много - книгата е голяма, обхваща много широк спектър неща и е достатъчно сложна. Основно търся детайли за различни неща, които смятам за нужни ми в някой момент, в Интернет. Много често ползвам материалите в ютуб-канала на eigenchris, но не само. https://m.youtube.com/watch?v=DvEdm6a-9Tw&pp=0gcJCR4Bo7VqN5tD Може но е вярно, специално за ротацията на Вик, която също може да се определи като ненужна на СТО, но на няколко места Скенер я дава като възможност за превръщане на диаграмата на декартова координатна система (евклидово пространство) в диаграма за пространство-време на Минковски (или по-скоро обратното). Според мен не работи, прекалено опростено е, превръщането на обичайна диаграма на декартова координатна система в пространствено-времева диаграма на Минковски е по-сложен процес и включва употребата на разслоение. Говорим просто за диаграмни преобразувания, а не за физически процеси (и само между другото - това нещо няма нищо общо с диаграмите на Епщайн и с Евклидовата относителност). Не можем просто така (примерно - чрез ротациите на Вик) да се прехвърлим от декартова координатна система към такава на Минковски, процедурата е по-сложна, ако искаме да я запазим смислена и логична. Написах повече за това в последния ми отговор до Скенер но в случая аз имам предвид, че при регистрация на местоположение на частица не могат да се дефинират нейни пространствени (3D) размери и затова наричам устоновеното месоположение точково. Предполагам това означава твърдението, че растиците (елементарните) са точкови, защото в случаите извън замерване/взаимодействие те нямат точно установени местоположения, камо ли пък собствени форми и размери.

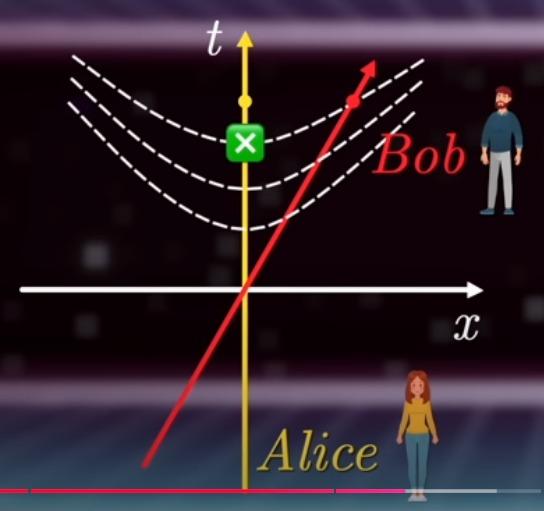
Доколкото си спомням, преди това (както и след това) протича еволюция във времето (на вектора на състоянието на частицата или още вълновата му функция), описвана от уравнението на Шрьодингер (нерелативистко, линейно, с унитарна, непрекъсната, детрминистична еволюция). При колапса на вълновата функция (редукцията на вектора на състоянието, което по-общо съответства на някакъв, обикновено ермитов оператор Q и на "скок" към някакво собствено негово състояние) - нелинеен процес, прекъснат, пробабилистичен. Това си спомням да беше най-доброто описание на състоянието на частица при и извън измерване или взаимодействие. Още не ми е ясно къде тук се вписва (как се тълкува) откритето на Златко Минев за "плавно", "непрекъснато" (без скок) променяне на енергийното ниво на атомите при облъчването им със съответната светлина.

Мога да я чета и като сложен, но общ сборник на редица базови неща, детайлите по които да трябва да се търсят от други източници (втората част от цитираното твое изречение). На мен ми изглежда, че ротацията на Вик си е направо некоректна. Може да се ползва например като нещо от рода на облекчаващ трик, но не и за коректно описание на СТО и на пространствено-времевата концепция (тълкува се като "изместване" на времевата координата ct от нейната, време-подобна област, в пространствено-подобната област на посоката на движение х). Какво е по-коректното представяне, което ти имаш предвид? Колапсът на вълновата функция не е ли точковото местоположение на частица (случаят, когато дадено поле и неговата вълна на вероятността се представят като частица)?

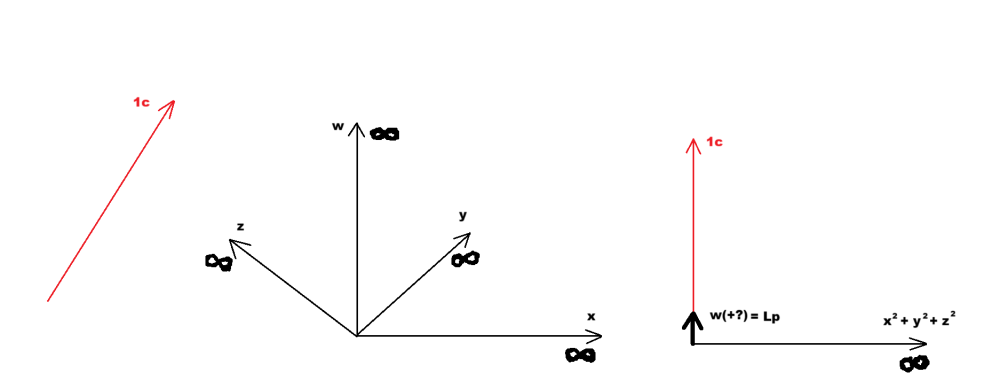
Да не цикля само с тая СТО (така абсолютно нищо няма да развия, даже и в най-най-груба форма) - бихме могли да кажем, че цялата реалност представлява вълти и полета (електро-магнитните и гравитационните вълни са ясни, пространствено-времевата кривина е като гравитационно поле, само не нютоново, а айнщайново, частиците се представят от квантовата механика като колапси на вълновата функция и като квантово-механични полета - същите, които предизвикват квантово-механичните флуктуации на околопланкови дължини). Тук веднага идва въпросът с масата в покой. Ето как се разсъждава принципно в тази връзка: https://profmattstrassler.com/articles-and-posts/some-speculative-theoretical-ideas-for-the-lhc/extra-dimensions/how-to-look-for-signs-of-extra-dimensions/ Подходът Калуца-Клайн и още повече суперструнната теория изискват още повече семейства с все по-масивни подобни една на друга частици в сравнение със сегашните четири (три семейства все по-масивни частици от всеки вид, плюс безмасовите). Твърди се (грубо казано), че допълнителни микроскопични измерения могат да се регистрират от 3D-логиката като все по-масивни много подобни една на друга частици. Движенията в допълнителни микроскопични измерения се регистрират от 3D-логиката като по-голяма маса. И така моментално идва въпросът, от движения къде идва масата на вече потвърдените елементарни частици, когато са в покой в 3D-пространството?

Това, че не те следвам сляпо, само защото ти си казал (написал) нещо не значи, че не ценя коментарите ти и не проверявам и пре-проверявам разни неща, които си споменавал (когато не се занимаваш с постоянни упреци, че не съм чел достатъчно от необятните простори но физиката, сякаш съм на някакъв изпит - и ти не си чел геополитически материали на Кисинджър, Бжежински, Хънтингтън, камо ли пък да ги разбираш, а аз съм ги чел). Ако търсиш религиозен поклонник - няма да съм аз! А книгата на Пенроуз не представя ли добре известни неща (от куп месеци чета основно нея, макар и не само)? Или простото не трябва да противореча, че теориите на относителността и квантовата механика са СВЕТАТА ИСТИНА, макар да не могат да се обединят продуктивно?! Виж предния ми отговор до Скенер. Вече попитах книгата на Пенроуз какво е. Вероятно и тя ще излезе популярна литература...

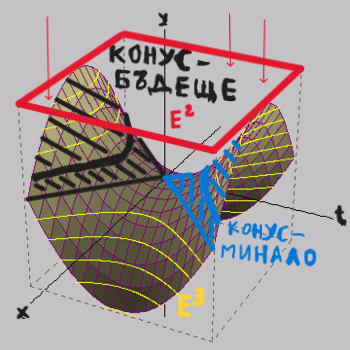
Придаването на комплексен характер на само една координата (времевата) въобще не води до преобразуване на пространствено-времева диаграма на Минковски в евклидова такава (нито на евклидова диаграма до пространствено-времева). Ти сам изброяваш недостатъците на ротацията на Вик (или на Уик - все едно!) при употребата и' за подобна цел. Пенроуз подхожда много по-пълноценно, като определя всичките пространствено-времеви координати като комплексни и след това извлича диаграмата на Минковски с нотация +--- чрез операция на комплексно спрягане С. Единствения смислен начин да преобразуваш обичайна диаграма с декартова координатна система и евклидовото пространство, което тя символизира, на псевдо-евклидовата пространствено-времева диаграма на Минковски е, като вложиш виктора на скоростта 1с (точно 1с, а не каквато и да било друга скорост) в обичайната декартова координатна система (евклидово пространство) и при това въпросния вектор на скоростта 1с оказва ефект на лоренцово скъсяване на дължината по своята посока. Така декартовата диаграма (евклидовото пространство) се деформира до познатото "седло" и се влага като "разкривено" ("седловидно") "вътрешно пространство", наблюдавано през евклидовия екран на диаграмата на Минковски. Така се стига до хиперболичната права, която може да се определи и като квадрант на хиперболична окръжност, която е свързана с въртенето на примовата координатна система при Минковски. Тука ротацията на Вик (употребата на имагинерната величина i ) не върши никаква работа, работа върши употребата на разслоение, чрез което въртенето на четиримерна декартова координатна система (евклидово пространство) спрямо вектора на скоростта 1с, всичкото това базис, проектира (чрез проекция - функция за преход между базиса и слоевете на разслоението) базовите вектори в основата на диаграмата на Минковски (пространство-времето на Минковски).

Ако правилно съм разбрал нещата с комплексните форми, практически имагинерната единица (корен квадратен от минус едно) се ползва за две неща - алгебрично да промени знака пред нещо (чрез умножаването на това нещо по имагинерната единица), а пък геометрично означава завъртане на 90 градуса. Ако това нещо не се прилага към фундаментални неща, тогава има и стандартна (некомплексна) процедура, чрез която да се получи същия резултат. Ако обаче се ползва за фундаментални неща (няма друго, стандаргно решение вместо комплексните практики и те са единствения вариант) - значи има някакви неясноти и скрити моменти, до които все още не се е достигнало по някаква причина. Например, употребата на i в ротацията на Вик (формулирането на ict). Нещата могат да бъдат описани и по този начин, и по обичайния начин (без употреба на i или гененерално - на комплексни форми). Кой е обичайния начин за превръщането на четиримерна декартова координатна система в пространствено-времева на Минковски? Има ли някаква подобна утвърдена процедура? Става дума просто за теоретическо преобразуване, а не специално за пространствени и непространствени измерения. Теоретична процедура без употреба на комплексни практики, чрез която стандартна декартова координатна система да стане координатна система на Минковски.

Със сигурност не владея материята уверено и затова пиша тук - да видя какво ще кажете онези, които сте по-напред от мен Няма нищо странно - има нещо, което ми е особено интересно в момента (пространствената хиперизмерност и нейната приложимост във физиката) и заради това чета много ховече, отколкото бих го правил, ако го нямаше този по-изразен конкретен интерес. Още в третото изречение на цитирания от теб мой текст съм написал, защо го наричам така - върти се във (или спрямо него се върти) четиримерна (тоест - хиперпространствена) декартова координатна система и затова става дума за вектор на четири-пространствена скорост (хиперизмерен вектор). Всичко, свързано с повече от три пространствени измерения е хиперизмерна логика, включително и четирите пространствени измерения. Векторите на едно-скорост, на две-скорост, на три-скорост не се различават помежду си така, както се различава от тях четири-скоростта. Тази разлика (защо реалността е четиримерна пространствено-времева, вместо четиримерна пространствена - примерно галилеево/нютоновата относителност) не е ясно обяснено откъде идва. Докато няма ясно обяснение на причината реалността на макрониво да е съвместима с пространствено-времевата псевдо-евклидова концепция вместо с чисто пространствена евклидова - със сигурност има проблем. Естествено - винаги можем да се престорим, че това не е проблем, че и така всичко си е съвършено, защото работи завидно добре и областите на неприложимост са ограничени (в случая - квантово-механичната област)...

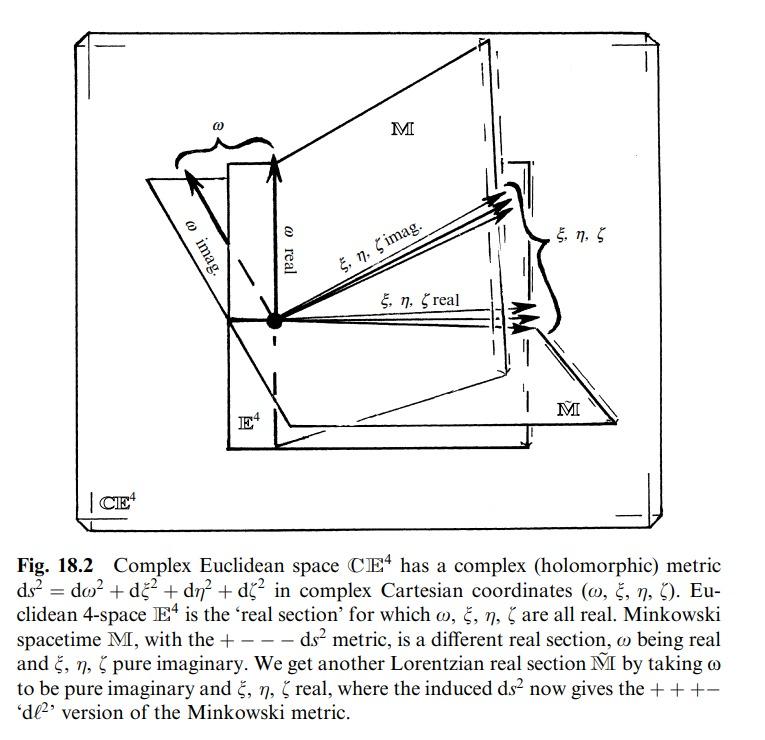
Доста неща при пространствено-времевата концепция са сложни, макар в рамките на самата концепция да намират някакви повече или по-малко витиевати решения. Парадоксът с близнаците също е подобен на тоя със скоростовия четири-вектор (и въбще - всички видове четири-вектори, дефинирани в СТО) и за него също се счита, че е напълно решен посредством пространствено-времевата логика. Пенроуз пък решава тези неща, като прави всичките четири пространствено-времеви координати комплексни и така изгражда комплексно евклидово четири-пространство, от което извлича, като подпространства (сечения), обичайно евклидово четиримерно пространство (за нотация ++++), обичайното пространство-време на Минковски (за нотацията +---) и трето, "лоренцово" пространство-време (за нотацията -+++).

Определено не е - заради това научих за физиката неща, които иначе никога не съм имал намерение да уча. Няма стимул да учиш вече известни неща, след като за всяко нещо си има утвърдени специалисти, чиито възможности ти най-често никога няма да достигнеш, без да си започнал от дете. Написал съм че е постулат. На практика, това е постулата за скоростта на светлината във вакуум на Айнщайн плюс вектора на четири-скоростта. Тук те са обединени като вектор в хиперизмерна, тоест четири-пространствена координатна система (затова и векторът е хиперизмерен). Това е същото като умножаването та t със скоростта на светлината, за да се уеднаквят мерните единици при диаграмата на Минковски и да се получат конусите под 45 градуса (без умножението на t по с конусите щяха да са почти хоризонтални, почти съвпадащи с х). Тук нещо подобно (съчетаването на вектор 1с с четиримерна декартова координата система) се ползва, за да се получи пространствено-времевата координатна система. Има скорост на светлината, а няма вектор на четири-скоростта, чрез който да се опише. Векторът на три-скоростта описва всички налични скорости в 3D-пространството, включително и тази на светлината, както и скорости, по-високи от тая на светлината. При вектора на три-скоростта парадокси няма.

Казва се, че не същества, понеже се стига до проблемната нулева стойност (която пък се получава заради нулата на собствето време при движения в 3D със скоростта на светлината - деленето на нула). Акцентирам на нулата на собственото време, защото тя произхожда от отказа от пространствен базов вектор в ползата на времеви базов вектор за изграждането на пространствено-вревите диаграми.

Аз подхождам по следния начин: Първо си задавам въпроса - по какъв начин трябва да се измени четиримерна обичайна евклидова, декартова координатна система, за да се получи пространствено-времевата координатна система на Минковски? Изменението е едно-единствено - въвеждането на хиперизмерния вектор на скоростта 1с. Чрез разполагането на обичайната декартова четиримерна координатна система спрямо този вектор (или пък обратното - на вектора 1с спрямо координатната система, но така се обособява специално място, докато при въртенето на координатната система спрямо вектора "специалното място" е вектора) се дефинират базовите вектори на пространствено-времевата диаграма на Минковски и така се изгражда въпросната диаграма. Това нещо може да се представи като разслоение (хиперизмерната координатна система и вектора на хиперизмерната скорост служат за дефинирането на базовите вектори на пространствено-времевата координатна система, което не е просто преход от една координатна система към друга и значи може да е разслоение). И макар това да е просто описание на два различни вида координатни системи (изцяло пространствена и пространствено-времева), може би има нещо на микроскопично (квантово) равнище, което налага употребата на четиримерната пространствено-времева диаграма на Минковски вместо обичайната декартова четиримерна координатна система.

Точен цитат от Уикипедия за четири-скоростта: "Четирикомпонентната скорост, дефинирана тук, използвайки собственото време на обект, не съществува за мирови линии за безмасови обекти, като фотони, движещи се със скоростта на светлината; нито е дефинирана за тахионни мирови линии, където тангентният вектор е пространственоподобен ." Накратко - причината за това значително разминаване на особеностите на четири-скоростта спрямо три-скоростта, което е вид парадокс (независимо от сравнително добрата обосновка на четири-скоростта чрез пространствено-времевата логика) е непространственото естество на четвъртото (времевото) измерение. Това различно естество на едно от всичките четири измерения води до явно различното естество и особености на скоростовия четири-вектор спрямо три-скоростовия му аналог.

И така - сменям маркетинговия подход (маркетингово ребрандиране), така да се каже! Повече тук няма да споменавам за диаграмата на Епщайн и за Евклидовата относителност. Аналогът на инвариантния, абсолютен вектор на хиперизмерната скорост 1с в стандартната пространствено-времева концепция на Специалната теория на относителността е векторът на четири-скоростта. Може да се каже, че той страда от парадокс - при неща, които се движат със скоростта на светлината (като светлината, например) стойността на четири-скоростта е НУЛА (заради нулевата стойност на собственото време Тау, което в този случай е нула, а от него се получава четири-скоростта). Така имаме уж-аналог на три-скоростта в 3D, но излиза стойност, която не отчита, че в 3D светлината се движи с 1с, а не с нула. Този парадокс навежда на подозрението, че има нещо не съвсем довършено в Специалната теория на относителността, макар най-вероятно такова твърдение да бъде яростно отричано. Всички са се примирили с този очевиден парадокс и му намират някакво хитроумно "обяснение", заради безспорните успехи на СТО в правилното обяснение на куп други неща. Парадоксът с "нулевата" четири-скорост може да намери обяснение чрез даването на пространствено естество на сегашното изкуствено четвърто измерение - времевото. Могат да се идентифицират две основни концепции – концепция на фундаменталния покой (Блоковата Вселена) и концепция на фундаменталното движение (хиперизмерния базис с абсолютно хиперизмерно движение). Между двете концепции има съответствие (всеки елемент на едната част от съответствието трябва да притежава някакво представление, даже и на пръв поглед съвсем несвързано или пък огледално-противоположно, в другата част от съответствието). Как би изглеждала връзката (проекцията - функция за свързване Р) между две координатни системи, от които едната се явява част от базис В, а другата е част от разслоение Е? Принципно, най-фундаменталният базис би трябвало да се крие на микроскопично (квантово) ниво и би трябвало да представлява идеална, безразмерна точка (заради концентрацията в едно място на всички възможни движения с 1с, което прави пространствените протяжности във всички възможни посоки нулеви, както липсва и време), 0-мерен скалар (тензор), тотална симетрия, тотално НИЩО, от която, чрез нарушаване на симетрията и проекции, произлизат всички необходими за описанието на реалността измерения. Това, обаче, е спекулация, която е все още много далече от що-годе по-детайлно очертаване. Засега базисът се състои от два постулата (вероятно всички това произлиза по някакъв начин от микроскопичното, квантово равнище, но понеже все още нямам достатъчна яснота, как би могло да се случва това, засега говорим само за постулати) – постулиране на вектор на инвариантната (абсолютна, винаги константна) хиперизмерна скорост 1с и постулиране на евклидова четиримерна координатна система (пространство) wxyz, протяжността на чиито базисни вектори (всички) е безкрайна. Става дума за изцяло пространствена координатна система, без никакви непространствени измерения. Когато напълно празното (без никакви обекти, движения и въобще каквото и да било в него) евклидово пространство (многообразие, координатна система) wxyz се съчетае с вектора на хиперизмерната скорост 1с, този вектор може да се върти в координатната система на това пространство (многообразие) или пък можем да кажем, че постулираната евклидова четиримерна координатна система се завърта спрямо вектора на хиперизмерната скорост 1с. Това съчетание се превръща в базис и по този начин се проектират (най-вероятно от микро- към макро-ниво) базовите вектори на стандартна пространствено-времева диаграма на Минковски, която пък се явява слой от пространствено-времевото разслоение на Специалната теория на относителността. Мировите линии са сечения през пространствено-времевото разслоение. При пространствено-времевото разслоение всеки отделен пространствено-времеви слой (всяко отделно пространство, многообразие) представлява отделен, уникален завършен цикъл (състояние) на Вселената, вследствие на късото (с планкова дължина) асиметрично пространствено отстояние на Вселената по направлението на координатата w при покой, което пространствено отстояние светлинната скорост на материята на Вселената изминава много бързо (за планковото време), докато по направленията х, у и z с тяхната безкрайна или наподобяваща безкрайност протяжност не е изминала почти нищо – завършен цикъл по w (кръг, който в добавка към останалите три измерения хуz става спирала), който постоянно води до нови и нови пространства, всяко с уникално състояние, до нови и нови версии на Вселената, до нови и нови уникални Вселени, което е и пространствено-времевото разслоение. Това е видът на "ребрандираната" ми концепция, без диаграми на Епщайн и Евклидови относителности.

Следвах твоята логика, че след като един подход има минуси, значи трябва да игнорираме плюсовете му и да го зачеркнем изцяло. Докато ОТО и квантовата механика не се обединят - няма подход само с плюсове, пък и тогава ще има практики с плюсове и минуси, предназначени да акцентират на определени неща, което ще е за сметка на други неща. Диаграмата на Минковски също има недостатъци - замъглява наличието на хиперизмерния вектор 1с (заради 45-та градуса по-малко, които ползва за своя квадрант на окръжност и от тук идва хиперболичното, неевклидово естество на диаграмата и наличието на "вътрешна кривина", когато се наблюдава от евклидова перспектива), макар него да си го има и там, само там е с различни дължини при различните ъгли на завъртането си. Така по-лесно се поддържа илюзията, че едва ли не не съществува абсолютно никакъв друг начин за представяне на всичко това, освен чрез употребата на изкуственото времево измерение (да започна да изкарвам разговора от тия проклети диаграми на Епщайн и Евклидови относителности, че даже и на мен вече започна да ми писва от постоянното циклене все с тях!). Имаше-имаше! Специално пишеше, че Грасмановите алгебри ли бяха там или нещо друго подобно са приложими при намирането на едни геометрични особености, а някакъв друг вид математически инструмент беше приложим за намирането на други особености от нещо важно - не мога да се сетя точно, четох го преди доста месеци. Имаше и още подобни примери, особено от квантовата механика... Сега не ми се търси точно за това! Със сигурност няма да приемеш никой от аргументите ми за постоянната употреба във физиката на разнообразни алгебрични, геометрични и теоретични инструменти с разни слабости и винаги ще намираш някакви оправдания за "съвършенството" им - това е ясно. Не отхвърлям нищо, вече в трети пост споменавам, че възнамерявам оттук-нататък да спра с употребата на диаграмите на Епщайн и на Евклидовата относителност, защото всичко разглеждано от мен (асиметричната пространствена хиперизмерност wxyz и т.н.) си го има и в диаграмите на Минковски, само там е по-трудно за открояване. Недобри са, само ако при употребата им не се държи ясна сметка за техните плюсове, минуси и ограничения. Но - какво значение има всичко това, след като всичко твърдяно от мен си го има и в диаграмата на Минковски (и нейния недостатък - там е много по-трудно за открояване, заради хиперболичното естество на диаграмата - употребата на хиперболична вместо на обичайната евклидова окръжност, заради 45-та градуса по-малко, които диаграмата ползва за представянето на въртенето на примовите координати)?!

Виж в какъв смисъл съм го написал. Никъде не съм написал, че матриците са безполезни и не трябва да се използват, само съм отбелязал техен недостатък спрямо диаграмите (конкретно - тая на Минковски). Но - ето ти още един пример: когато става дума за извършване на действие върху формули, съдържащи познати функции, интегрирането е "трудно", като в много случаи не може да бъде извършено в явен вид (извадка от книгата на Пенроуз "Пътят към реалността", шеста глава, Реален математически анализ, Какви качества трябва да има една истинска функция, стр. 139). Това е фундаментален недостатък на интегрирането, значи - да го зачертаем и него като носещо някакви ползи поне там, където е приложимо, нали? (Забавното: и тук има огледален елемент - според фундаменталната теорема на анализа диференцирането и интегрирането са огледални една на друга процедури!) Могат да се дадат още куп други примери, където някакви математически и геометрични инструменти вършат работа само ограничено (за някои неща, а за други се провалят), сега не ми се търси, знаеш, че ще намеря още купища такива примери... Поне виж какво е написал Скенер - последния му коментар тук наистина е пълноценен и отлично структуриран. Там ясно е написано, че диаграмата на Епщайн (това не е Евклидовата относителност - допълващи интерпретации, част от които произхождат от самия Епщайн) е приложима за едни неща и се проваля в други неща. Диаграмата е използваема, макар и ограничено, както куп други неща, преди ОТО и квантовата механика да се обединят успешно (тогава вече няма да има уравнения, които да се нуждаят от ренормализация). Виж колко точен бях относно диаграмите на Епщайн - толкова са ти противни, че се опитваш да отречеш абсолютно всякаква тяхна полезност, дори и частична и при това при условие, че заявих отказ да ги споменавам в следващи мои коментари, макар аз да продължа да си ги ползвам, когато счета, че могат да ми бъдат полезни с нещо! Това като че ли е малко прекалено (или поне не е най-точно казано обективно). От отлично балансирания коментар на Скенер има какво да се научи...

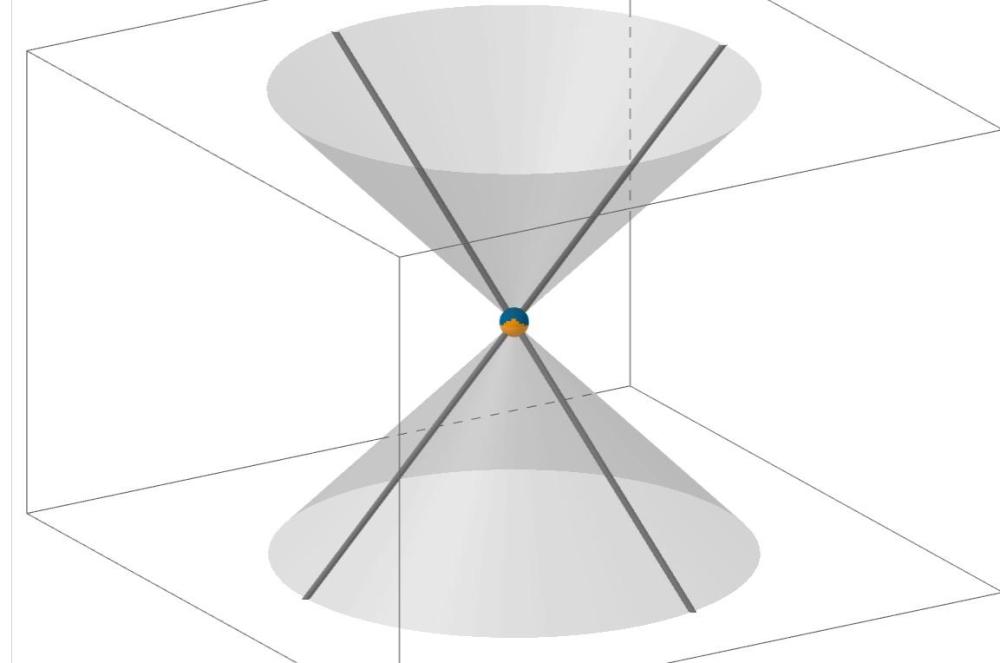
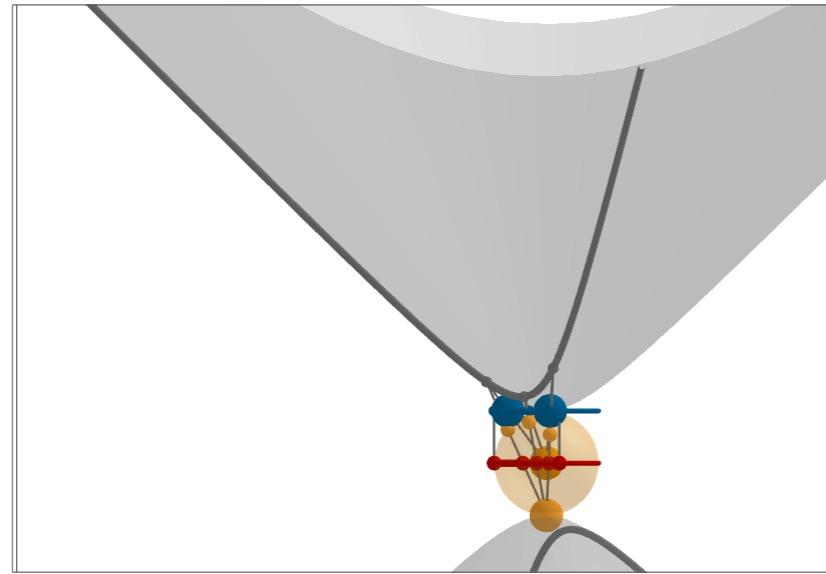
Матрица: Диаграма на Минковски: Наистина ли не виждаш разлика в количеството показано без допълнителни операции в двата случая?! Диаграмата на Минковски според теб не показва повече с един поглед, без допълнителни сметки и писане, от матрицата (таблицата)?! Еми...

Във физиката редовно се ползват матриците. Грубо казано - това са таблици и като такива те страдат от страшно много ограничения. Купищата неща (физически параметри и закономерности), които могат да се представят визуално наведнъж чрез една диаграма на Минковски, чрез матриците могат да се представят само след цял куп допълнителни операции, произтичащи от линейната алгебра. Тези безспорни ограничения на матриците (таблиците) спрямо диаграмите на Минковски въобще не водят до чак такава съпротива за употребата на матриците във физиката, както съпротивата срещу диаграмите на Епщайн заради техните ограничения. Радикална съпротива срещу диаграмите на Епщайн, въпреки че в актуалната физика най-редовно се ползват купища средства с ограничения там, където силните им страни могат да донесат полза. Самите Обща теория на относителността и Квантова механика са средства с ясно очертани ограничения, което никак не пречи да бъдат постоянно използвани там, където силните им страни дават търсените резултати. Ползата от диаграмата на Епщайн е тази, че ясно откроява ключовата роля на хипер-измерния вектор 1с за описването на реалността чрез четири пространствени измерения. (Специално подчертавам, че тук не се отрича възможността да се описва реалността И чрез НЕпространствени измерения, а само се търси начина, по който описанията И с непространствени измерения могат да се преобразуват в описания САМО с пространствени измерения.) Дали ще изберем диаграмата на Минковски и стандартната (псевдо-евклидова) специална относителност или диаграмата на Епщайн и Евклидовата относителност е последващ въпрос, преди който има нещо друго, по-ключово, до обсъждания на което въобще не може да се стигне заради ступора и съпротивата моментално, щом бъдат споменати диаграмите на Епщайн и Евклидовата относителност. Добре! Мога въобще да не споменавам диаграмите на Епщайн и Евклидовата относителност, щом са чак толкова недолюбвани заради ограниченията им (зная за част от ограниченията, които Скенер е споменал в последния си пост и съм му благодарен за ясната систематизация и разяснения - разбирам почти всичко /симетриите все още не са ми особено ясни и не се оправям с тях така, както ми се иска/ и написаното в поста на Скенер ми е много полезно). Всичко това (и псевдо-евклидова относителност на Минковски, и евклидова относителност на Епщайн) произлиза от базиса на хипер-измерното пространство wxyz, от който чрез разположението на хипер-измерния вектор 1с се определя начина, по който се проектират базисните вектори, които изграждат координатните системи, които искаме да използваме (били те тези на Минковски, били на Епщайн - дали искаме да ползваме координатното или собственото време като вертикална координата е последващ момент). От базиса на хипер-измерното пространство wxyz, посредством проекции чрез разположението на хипер-измерния вектор 1с, се проектира разслоението на пространство-времето на Минковски, където мировите линии са сечения през това разслоение. Универсалната (единствена) хипер-измерна скорост 1с се разлага на своите пространствена и времева компонента и така се изгражда пространствено-времевата концепция на Минковски.