Станислав Янков
Потребител-
Брой отговори
2763 -
Регистрация
-
Последен вход
-
Days Won
1
Content Type
Профили
Форуми
Библиотека
Articles
Блогове
ВСИЧКО ПУБЛИКУВАНО ОТ Станислав Янков
-
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
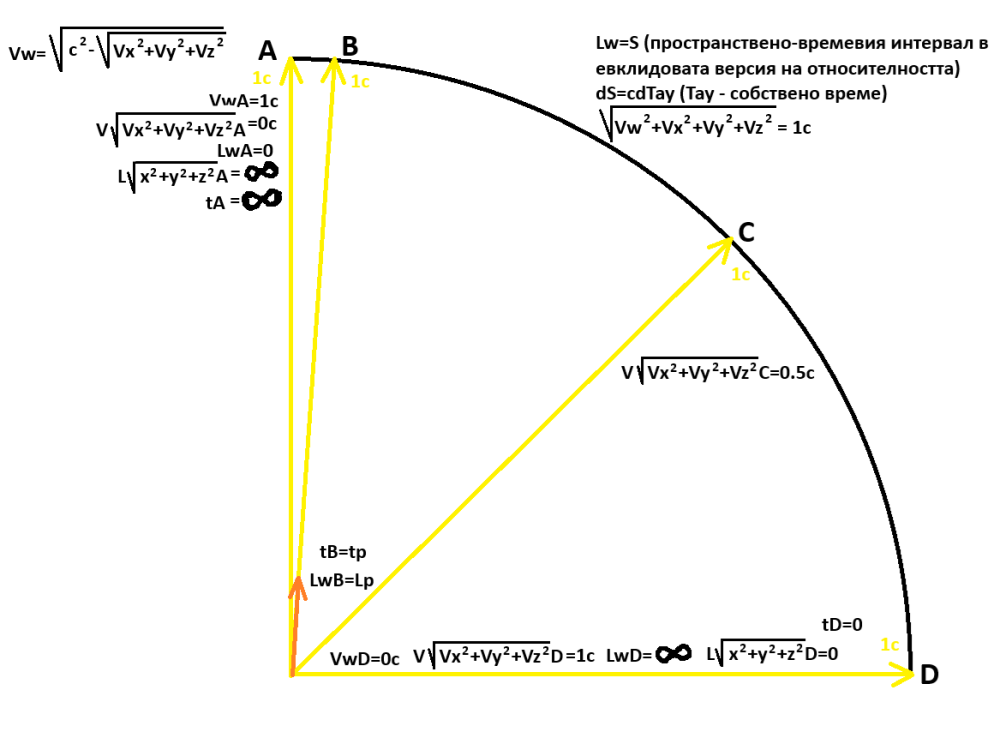
Имам някои първоначални допускания. Ако векторът на скоростта 1с е вертикално нагоре по координатата на измерение w, времето би имало стойност безкрайност, което може да се тълкува като регистрация на всичко (минало настояще и бъдеще) едновременно. За да може да има някакъв часовников темп (като максималният темп в покой, равен на планковото време - не може да съществува времеви отрязък, по-кратък от планковото време, само по-дълги), векторът на скоростта 1c не трябва да е вертикално нагоре, а много малко вдясно. При преминаване на частица през два отвора се казва, че тя (нейната вълна на вероятността) интерферира със самата себе си. Не би ли могло да става дума за версии на частицата от околното ѝ (за съответния момент) минало и/или бъдеще и това да е нейния вълнови пакет? Но, засега това е просто с нищо неподкрепена спекулация, която да проверявам с евентуално нарастване на знанията ми по квантова механика в бъдеще. Знанията ми, не само за КМ, ще нарастват постепенно заради вманиачаването ми по възможността за изграждане на физика без измерения, различни от пространствени. Възможно или не - ако не беше това вманиачаване, никога нямаше да зная за физиката толкова, колкото зная днес (независимо колко малки изглежда да са знанията ми отстрани). Допреди да се вманиача по това, плановете ми относно физиката бяха книги МАКСИМУМ като тия на Браян Грийн (това бяха книгите, които създадоха първоначалния ми, ненулев интерес към физиката, но нищо повече - допреди две години нямах никакво намерение да купувам книга като тая на Пенроуз). Сега обаче - на работа (и днес е работен ден)! -
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
Противно на твоите и на Гравити представи - аз чета ВСИЧКО, адресирано до мен и особено внимателно чета нещата, които пишете двамата с Гравити, включително и когато не са адресирани до мен. Проблемът ми е, че физиката е НЕОБЯТНА, БУКВАЛНО, не е и никак лесна, а само от книгата на Пенроуз научих за термини и интерпретации, за които не бях чувал АБСОЛЮТНО НИЩО преди това и те са буквално стотици (гарантирано поне над 200 - започнах буквално от нулата преди няколко години, с първите ми изяви тук). Дори не мога да запомня голяма част от всички тези НАПЪЛНО НЕПОЗНАТИ доскоро за мен неща (не съм записващо устройство), камо ли пък лесно да разбера взаимовръзките между тях и нещата, които успях да понауча с времето, какво остава пък за взаимовръзките между всичките доскоро съвършено непознати за мен неща между тях самите (постоянно се оказва, че нещата не са точно така, както си мисля първоначално). Няма как да ви отговарям на двамата с Гравити на високото ниво, на което сте двамата, след като съм и още дълго ще остана далече от вашето ниво, освен това една част от коментарите написах днес сутринта, малко преди да тръгна за работа и друга част от коментарите (включително този, на който си отговорил сега) писах по време на работа, през малкото пролуки, през които успях да погледна малко по-внимателно написаното от вас (и от Шпага). Тълкувайте го с Гравити както си щете и ми вярвайте, ако щете, но - АЗ ЧЕТА ВСИЧКО, НАПИСАНО ОТ ВАС КЪМ МЕН И ГО ЧЕТА НАЙ-ВНИМАТЕЛНО, ДОКОЛКОТО МИ Е ВЪВ ВЪЗМОЖНОСТИТЕ! Няма нужда да се държите така, все едно полагате сериозни усилия (а вие полагате такива, особено ти), пък аз въобще не ви отчитам, защото това НЕ Е ВЯРНО! Сега по същество! Виж и следващите ми два коментара до теб, след този, на който си отговорил и ако прецениш - напиши нещо и по тях. След утре следват няколко почивни дни и ГАРАНТИРАНО ЩЕ ПРЕГЛЕДАМ (И ПРЕ-ПРЕГЛЕДАМ) ВСИЧКО НАПИСАНО НАЙ-ВНИМАТЕЛНО! Въпросът не е в някакви мои увличания по новото, без да познавам особено добре (да не кажем - почти никак!) старото, а в това, че за да успея да изследвам моята мания (възможността за съставяне на физика без непространствени измерения), аз трябва да изградя някаква най-първична обща концепция, след което вече да има нещо първоначално, което да усъвършенствам и допълвам с все по-тънки и обработени детайли. Трябва ми първоначална, дори и най-груба и необработена база, каквато в момента все още нямам. СТО криво-ляво е вписано в това все още грубо образувание (със сигурност има все още много-много-много какво да се подобри, но поне вече има някаква, макар и много груба, основа, която по-нататъка да се допълва и усъвършенства), но ти самият отбелязваш, че все още нямам практически НИЩО относно ОТО и квантовата механика и това наистина е ГОЛЯМ ПРОБЛЕМ! Няма смисъл да затъвам във всевъзможни все по-тънки детайли само в една област (примерно - СТО), докато не съм изградил поне нещо първоначално в останалите не по-малко важни области (ОТО и КМ). Всичко това не значи, че не обръщам достатъчно внимание на критиките ви - ОБРЪЩАМ! Просто - не мога да отговоря на всичките най-различни детайли, които ми търсите, без все още да съм си съставил поне някаква първоначална концепция относно ОТО и КМ, поне в най-груби очертания, каквито вече има относно СТО. Не че не искам, че не уважавам усилията ви да пишете и обяснявате, а просто - НЕ МОГА ЗАСЕГА! Не знам достатъчно, за да успея да отговоря на всичко написано от вас така, както очаквате. Благодаря за всички усилия и отговори, особено за вашите с Гравити и това е най-искрено! -
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
Тук съм сгрешил - не срез, а СЕЧЕНИЕ! (Така подчертано би трябвало да ми направи достатъчно впечатление, за да не го бъркам пак в бъдеще.) -
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
Щом е пространство-време - значи ще е 4D+1D (или още 5n-1). -
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
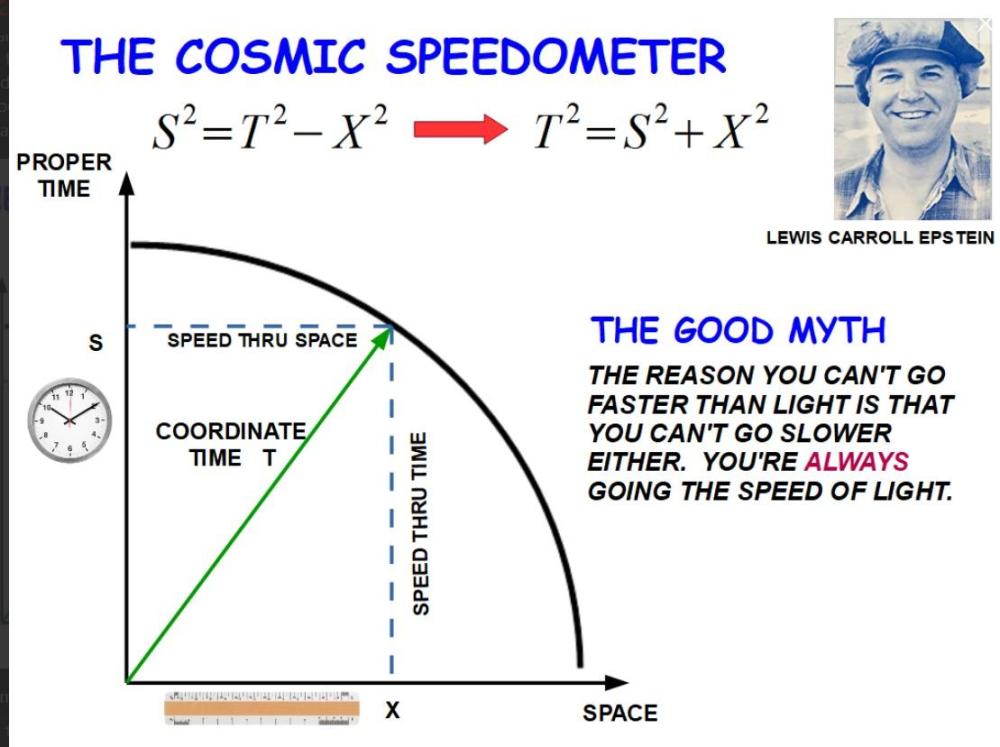
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
Приемането на времето като параметър, вместо като измерение, не прави този параметър абсолютен. Времето може и да си е параметър (компонент на базов вектов), и да се променя от координатна система към друга, когато двете се движат една спрямо друга (контравариантността на компонентите, която включва възможността техните стойности да са и различни в различните координатни системи). Диаграмата на Епщайн сама по себе си не е свързана със знака на метриката, това е просто диаграма, която променя акцента от координатното време на собственото време. Уеднаквяването на знаците във формулата за интервала е последващо развитие отвъд диаграмата на Епщайн, наричано Евклидова относителност (Euclidean relativity) и то наистина е недовършено без ясно дефиниране на базовите вектори (те се дефинират чрез разположението на вектора на хиперизмерната скорост 1с спрямо четирите пространствени координати wxyz и това е нещо, което досега не съм срещал никъде другаде, преди аз да го отбележа в този форум). Да, това е реален проблем на Евклидовата относителност и той се решава чрез ясното дефиниране на базовите вектори, които изграждат координатните системи (вече споменах за това по-горе). В пълноценния си вид всяко нещо от пространствено-времевото тълкувание си има алтернативно тълкование, макар и различно (най-често - някакъв вид огледално). Проблемът за прилагането на различния подход към ОТО наистина е много сериозен (аз все още не съм успял да откроя точната аналогия), на първо място заради привидната нужда от вкарване на още едно, пето измерение. Би могло пространствено-времевата кривина от ОТО да се представи чрез пространствено огъване по направлението на четвъртото пространствено измерение на фона на прави (с безкраен радиус) три останали измерения, засега това са все още мои в значителна степен произволни спекулации. Още нямам повече или по-малко годно решение за начина на прилагане на този подход към ОТО и квантовата механика, но мисля над това. Това се представя много лесно с уточнението, че при покой протяжността на Вселената по направлението на измерението w е с планковата дължина и всеки път, щом тази протяжност бъде измината от материята на Вселената със скоростта на светлината - започва нов цикъл, следващ кръг. Така всеки такъв нов цикъл е ново пространство, ново, следващо уникално и неповторимо състояние на Вселената и затова мировата линия е срез през разслоение, всеки от чиито слоеве е различно пространство (различно, ново и уникално състояние на Вселената, различна, нова Вселена). На всичко пространствено-времево може да се намери алтернатива, но въобще не е лесно и затова и няма много мераклии да се занимават с това. Много по-комфортно е само да се изучава вече утвърденото - то е много и е сложно и това е добро оправдание... -
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
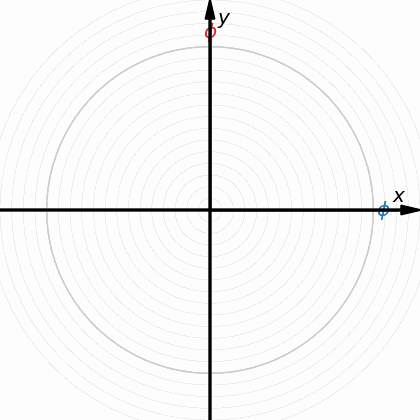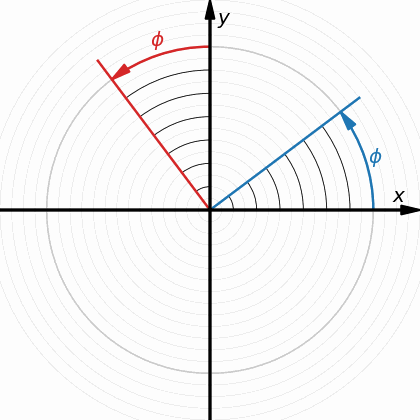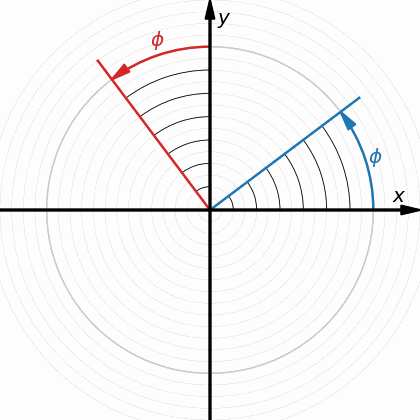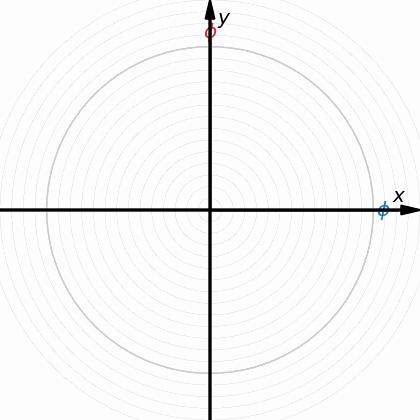
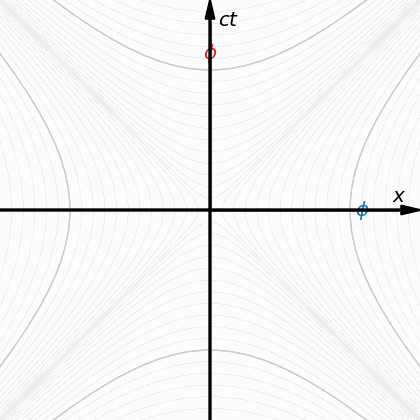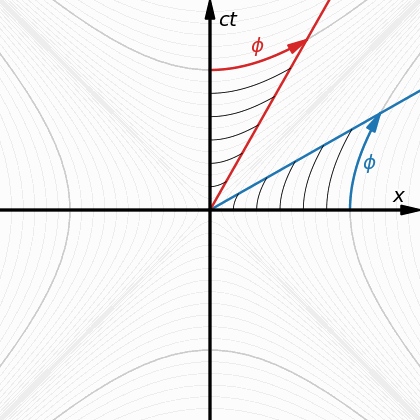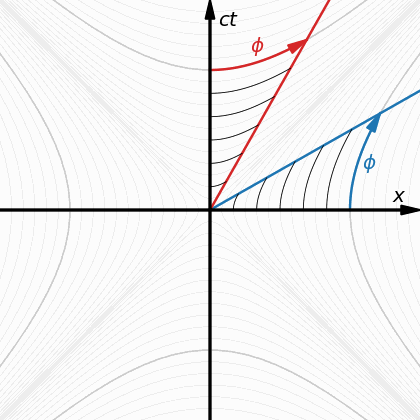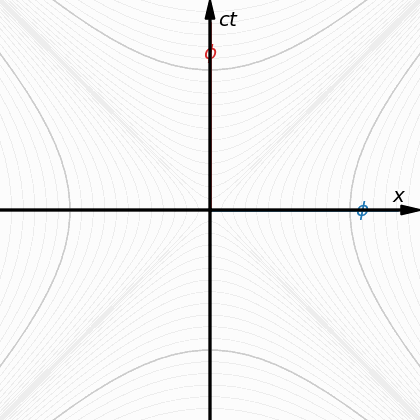
Нищо не се губи. При едната диаграма квадрант от кръг се представя чрез част от хиперболична окръжност, защото там въртенето се ограничава до диагонала от 45 градуса, докато при диаграмата с евклидова окръжност е пълни 90 градуса. Затова при пространствено-времевата диаграма на Минковски лоренцовите стойности се представят чрез хиперболична, вместо чрез обичайна евклидова окръжност - за да се компенсират липсващите 45 градуса в хиперболичния случай с конусите. Стойностите и в двата случая са едни и същи - и двете диаграми дават верните стойности, само едната го прави чрез квадрант от хиперболична окръжност вместо чрез такъв от обичайна евклидова окръжност, заради 45-те градуса по-малко за завъртането на примовите координатнати, за разлика от квадранта с обичайния евклидов кръг, където завъртането на примовите координати е до обичайните 90 градуса. -
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
Скенер ще си ти отговори отделно, аз само ще маркирам, че когато умножиш сt с имагинерната единица i (корен квадратен от -1), така практически променяш знака пред сt от минус на плюс и всички знаци във формурата за интервала стават + (+сt+x+y+z). (На някои места тази операция се нарича ротация на Уик.) Така обаче се губи реалния физически смисъл, защото по подобен изкуствен начин движенията в диаграмата на Минковски се прехвърлят извън конусите на Минковски, в областта на дължината l, вместо в тази на времето t (времеподбните стойности), която се очертава от конусите на Минковски. Един вид - по изкуствен начин времеви параметри се прехвърлят в областта на 3D-пространството. Именно наличието на времеподобни (отрицателни), светлоподобни (нулеви) и пространственоподобни (положителни) особености прави геометрията псевдо-евклидова. Пространствено-подобните характеристики имаха някакво отношение към собствената дължина (Proper Length), но този момент не го разбирам достатъчно добре, за да се опитвам да го обясня. -
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
Как само не щеш да отговориш ясно на това, което съм те попитал (защо може да включваме всякакви други измерения, освен пространствените и времевото и може специалната теория на относителността на Айнщайн да си функционира съвсем нормално и без времево измерение, само с постулати, но нямаме право да ползваме друга алтернативна концепция само с пространствени измерения и без времево такова)! Ще ти отговоря, след като получа ясен отговор от теб на моя въпрос. -
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
Прочетох ги, но всичко това е от пространствено-времевата концепция. Все едно с аргументи от квантовата механика да отричаш теорията на относителността или обратното. Затова се опитвам да минем по нещата стъпка по стъпка, за да видя, с кое точно си съгласен и с кое точно не си, освен че явно не си съгласен с генералната посока на алтернативата. Според теб демонстрират ли и двете диаграми верните стойности? Според мен - да! Няма никакво значение, дали събираш двете примови координати (времевата и хиксовата) към диагонала от 45 градуса или завърташ под точно същия ъгъл хиксовата ос надолу - и в двата случая основния времеви интервал се удължава, когато се проектира върху завъртяната примовата времева ос, а примовата дължина по посока на движението се съкращава, когато се проектира върху върху основната хиксова ос - и в двата случая е едно и също, нали? -
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
Следя го, ти постоянно клинчиш! Един път може да има само пространство-време като измерения, друг път може да има други измерения, освен пространствени и времеви (тогава няма да е пространство-време, а нещо друго и явно според Скенер няма никакви проблеми да има и такива други неща, както вероятно и според теб), обаче ВЪОБЩЕ НЕ МОЖЕ ДА ИМА само пространствени, без никакви други измерения, макар и да го има под формата на айнщайновата специална теория само с постулати и само пространствени измерения, без времево... Следя го разговора и го следя много внимателно, както и постоянно си припомням стари ваши обяснения със Скенер (споделяни или не от мен разни елементи от тези обяснения, те са ценни и периодични си ги преповтарям, тъкмо и да проверя, как са се изменили знанията ми с времето - не съм съвършен, бавно е, но се развивам)... -
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
Тоест, колко са измеренията все пак има значение - при повече от четири измерения има нерешими проблеми при досегашните над-четиримерни концепции. Логично е вътрешните свойства при различни броеве пространствено-времеви измерения да се запазват еднакви (като n-1 мисля, че се означаваха пространствено-времевите измерения) - всичко това са един и същи тип концепции, пространствено-времеви. За да се измени естеството на вътрешните свойства - трябва да се напусне пространствено-времевата концепция. А ако включва и нещо друго като измерение, освен пространството и времето? Нямам предвид конфигурационното и фазовото пространство (3n и 6n, като в случая n е броят изследвани обекти), условно пространство с три пространствени, едно времево и да кажем едно температурно измерение? Защото, ето какво ми е отговарял Скенер някога: "(По въпроса за "пространствените" координати. Пространството обединява степени на свобода, и не е задължително всяка от тях да има размерност 'метър'. Във фазовото пространство например се срещат и скорост, и термпература, и какво ли не като 'измерения'. За това и времето може да е 'измерение', координата.)." -
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
Ето това, Скенер, е напълно голо твърдение, просто защото ти се иска да е така! Покажи ми, къде толкова е тази фатална разлика, заради която само пространство-времето да е вярната концепция? На кое точно от ТО не може да се намери аналог чрез четири пространствени измерения? Не, че засега подобна концепция все още не е особено развита, че е само в зачатък - това аз самия винаги съм го твърдял, както и другото, че сам не мога да стигна твърде далеч и че точно аз не съм най-подходящия за тази работа (но щом като няма друг...)! Но, кое точно е невярното? Предполагам, че за диаграмите няма да отречеш, че са верни - още някога, преди година, Гравити и Кипен потвърдиха верността и аналогичността им: Дали примовата координатна система се върти по хиперболичен или по евклидов кръг спрямо основната - ефектите са едни и същи - времевият интервал се удължава (часовниците се забавят) и дължините се скъсяват и в двата случая. Предполагам, че тука няма забележки! -
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
Не е без значение - досега концепциите с повече от четири измерения (пространствено-времеви) се провалят. Понятието "измерение" може да бъде и широко (да включва и време, и температура, и какви ли не още неща - при едни разсъждения на Хокинг си спомням нещо за употребата на температурата като измерение), а може да бъде и тясно (примерно - измеренията да могат да бъдат само с пространствено естество). Това е въпрос на концепция, която е избрана - СТО с постулати и без време като измерение/СТО като пространство-време на Минковски... -
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
Защо да не е успех?! Различно е, трето, дава същите отговори, какво повече?! Да, не отрича нищо на пространство-времето, не го отхвърля, както теорията на Айнщайн е заместила нютоновата, но какво от това - един по-различен равностоен поглед! Точно затова говорим за съответствие - всичко е по-различно, почти огледално на пространствено-времевия подход, но и тясно свързано по този огледален начин. Статичния самун на Блоковата вселена е хиперизмерен вектор с константна скорост 1с, пространствено-времевите срезове са 3D-проекции на движения във времето, нещата, които са симетрични в единия случай не са симетрични в другия случай... Това, че е коренно различна логика и изисква значителни предефиниции на много неща (но всяка закономерност от едната страна на съответствието си има някаква различна закономерност от другата страна) не значи, задължително НЕ ТРЯБВА да се развива и този начин, въпреки че може! Базовият вектор w на движеща се с някаква скорост координатна система (пространство) се удължава спрямо координатната система на наблюдателя в покой, където е равен на планковата дължина, часовниците трябва да изминават повече пространство по четвъртото измерение и се забавят от гледна точка на неподвижния наблюдател (когато се сравнят). В същото време наблюдавания обект също счита себе си за неподвижен и от негова гледна точка базовият вектор w на неговата координатна система (на неговото пространство) също е с минималната си възможна дължина (планковата) и часовниците му се движат с максималния си възможен темп (този в покой), точно както е и при наблюдателя. Наблюдателят, обаче, регистрира координатната система (пространството) на движещия се спрямо него обект завъртяна (по хиперболичен кръг при пространство-времето или по обичаен евклидов кръг при изцяло пространствената концепция) и така регистрира и разликата в базовите вектори на подвижния обект, а от там и в компонентите на тези базови вектори - замерваните дължини и стойности на часовници... Всичко съвпада по огледален начин с пространство-времето, само базовите вектори на четирите пространствени измерения не са произволни, а в покой подържат определено съотношение помежду си (протяжността по координатата w е с планковата дължина, докато протяжността по координатите х, у и z е с безкрайна или с клоняща към (наподобяваща на) безкрайност дължина. Нищо повече! Всичко останало е толкова подобно, че двете концепции (пространствено-времевата и чисто пространствената) напълно съответстват една на друга, макар и по огледален начин! Не виждам никакви проблеми, особено пък такива, свързани с разни подробности, които да не могат да се разрешат с дребни корекции и усъвършенствания (развиването на концепцията, което засега осъществявам само аз, доколкото мога и затова напредъка е много бавен - мога доста малко, заради недостатъчните ми познания). -
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
Може да се състави и трета равностойна интерпретация (не по-добра, но и не по-лоша - равностойна, еквивалентна, съответствие), при която пространствените измерения са четири, времето не е измерение (то е много други неща, но в случая е просто параметър) и отговорите за замерванията са точно същите, които се дават и от Лоренцовите трансформации. Ако държим да е пространствено-времевия подход - това е лявата част на съответствието и там протяжността по направлението на едното пространствено измерение, която в покой е различна от протяжностите по направленията на останалите три измерения, се преформулира на времево измерение, а четвъртото пространствено измерение изчезва. При интерпретацията, където четвъртото пространствено измерение присъства, то също е напълно равностойно на останалите три, точно както е напълно равностойно на тях и времевото измерение, само четвъртото пространствено измерение е с различна пространствена протяжност по своето направление, заради хиперизмерния вектор 1с, точно както и времевото измерение не е пространствено, макар и да е равностойно на останалите три. -
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
Защо първоначалната айнщайнова концепция за относителността, преди да се намеси Минковски, си работи съвсем нормално без времето като измерение, ако времето толкова неизбежно е измерение математически и физически? Може свободно да се избира първоначалния айнщайнов подход без време като измерение или подхода на Минковски с време като измерение и двата подхода ще си дават съвсем верни, еднакви резултати при измерванията. Всичко е въпрос на избор на концепцията - пространствено-времева или не. -
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
Пространствено-времевата кривина какво пространство изкривява? Не е ли вътрешно свойство на ОТО? Мога да избегна времето като измерение, въпрос на концепция е. Защо времето не присъства сред степените на свобода (те са шест - три транслационни и три ротационни)? Всичко зависи от избраната концепция. Ако концепцията приема само пространствени измерения - времето няма да е измерение, а параметър. Никой-никъде не казва да няма време, а само какво не може да е. И при първоначалния айнщайнов, не пространствено-времеви на Минковски, подход, времето не е измерение и лично Скенер многократно е обяснявал, че от това относителността на Айнщайн и Лоренцовите трансформации не страдат по никакъв начин. -
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
Няма разлика, когато говорим за n+1 измерения, тоест - за пространство-времена. Употребата на времето като условно измерение вместо на пространствено измерение на мястото на времевото е удобно, защото е по-близо до ежедневния опит и донякъде облекчава вникването в като цяло НЕинтуитивните концепции с повече от три измерения (самото пространство-време въобще не е лесно/интуитивно за разбиране), спестява множество сложни главоблъсканици с пространствената хиперизмерност, обаче при пространство-време не може да се избегне някои неща да не могат да бъдат представени чрез пространствена геометрия. Например гравитационната кривина на пространство-времето няма как да е пространствена особеност (пространствено изкривяване), защото включва в геометрията си непространственото времево измерение и така в тримерното пространство не говорим за някакво пространствено изкривяване, а за движение с ускорение към масивен център. Ако говорехме само за пространствени измерения, тогава можеше да има реално изкривяване на пространствена геометрия - в областта на четвъртото пространствено измерение и в 3D-пространството това да се регистрира като движение с ускорение към масивния център. Това, че ползваме четиримерно пространство-време налага някои неща да се представят като "вътрешни" свойства и параметри, докато при пълноценно (но не евклидово, а проективно асиметрично) четиримерно пространство част от тези "вътрешни" особености могат да се представят като геометрия на пространството. Но дори и пространствено-времеви, броят на допълнителните измерения не може да бъде произволен (справка - проблемите при струнните и Калуца-Клайн теориите). Затова засега аз се ограничавам до четири измерения. Ако са повече от четири - механизмът явно не е струнния или на Калуца-Клайн, а някакъв друг, все още неоткрит. -
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
При пространство-времето пространствените измерения са само три (времевото измерение не е пространствено). Тогава множество неща, които при повече от три пространствени измерения биха могли да се представят по някакви различни, геометрични начини, при 3D+1D пространство-време могат да се представят само чрез разни "вътрешни свойства". Такива "вътрешни свойства" са кривината на пространство-времето от общата теория на относителността (именно заради нея се налага употребата на оператори и в ОТО, не само в квантовата механика), "вътрешните свойства" на точковите (безразмерни или още 0-мерни пространствено) елементарни частици в квантовата механика, калибровъчните подходи не само в квантовата механика, но налични дори и в електро-магнитната теория на Максуел (ако исках да се заяждам, щях да твърдя, че калибровъчните подходи са нефалсифицируеми и от там и неверни, измислици, понеже притежават особености, които са невъзможни за физическа регистрация/замерване). Лявата част на съответствието, което се опитвам да развия, най-стриктно следва пространствено-времевия подход на Минковски (3D+1D) и там не може да се мине без употребата на всичките тези "вътрешни" особености - те са неразделна част от стандартната физика днес. -
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
Ето едно място (няколко линка от него) с отлични обяснения как се разсъждава за допълнителни измерения (не само пространствени) и относно Калуца-Клайн: Extra Dimensions – Of Particular Significance Extra Dimensions – How to Think About Them – Of Particular Significance Dimensions of Physical Space – Of Particular Significance What is an “Extra” Dimension? Some Examples – Of Particular Significance Worlds of 1 Spatial Dimension – Of Particular Significance Worlds of 2 Spatial Dimensions – Of Particular Significance How to Look for Signs of Extra Dimensions – Of Particular Significance Kaluza-Klein Partners — Why? Step 1 – Of Particular Significance Kaluza-Klein Partners — Why? Step 2 – Of Particular Significance Голямата разлика между подхода на Калуца-Клайн (който се е провалил - дефинираните от теорията скаларно поле и "Дилатон", резонанси и други детайли не съвпадат с регистрираната реалност) и асиметричния четиримерен подход от съответствието, което застъпвам, е в това, че подходът на Калуца-Клайн е пространствено-времеви и от там идва неговата петизмерност (въвеждане на допълнителна степен на свобода, която усложнява и обърква нещата), докато асиметричния чисто пространствен подход остава (засега!) четиримерен (може да има начини за обясняване на гравитацията в рамките на четири пространствени измерения - "кривините" на ОТО да са "скрити" в увиване на асиметричното четвърто пространствено измерение w, което да води до регистрацията на гравитационното ускорение в 3D+1D пространство-време). В съвсем обичайната Специална теория на относителността има подсказка за произхода на съвсем обичайната маса в покой на отдавна установените частици от движения на вселенската материя в четвърто пространствено измерение - компонентът Р0 на четириимпулса, свързан с сt. Р0 е равен на масата, умножена на сt, цялото това - разделено на Тау (виж долното видео). Това означава, че масата в покой се формира от компонента на четириимпулса, свързан с сt (или още х0), скоростта на светлината с, координатното време t и собственото време Тау (да не забравяме, че при чисто пространствената част от съответствието Симетрично (плоско) 3D+1D пространство-време/несиметрично 4D-пространство времето НЕ е измерение/координата на измерение, а произлиза от асиметрията между пространствената протяжност по направлението на пространствената координата w и останалите три пространствени координати хуz, допълнена от някакви квантово-механични и термодинамични особености /ентропията/). -
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
Както всеки произволен обект, който се движи спрямо наблюдател с някаква скорост между 0с-1с, има собствено 3D+1D пространство-време/4D-пространство (съответствието, като при 0с собствените пространство-времена/пространства/координатни системи на "покоящия наблюдател" и "наблюдавания обект" се приравняват/сливат едно с друго), така и различните полета представляват пространство-времена/пространства с най-различни собствени характеристики на базовите вектори/измеренията. В тази връзка, не мога да се сетя, дали някъде съм срещал нещо за персонални обектови полета (персонални полета на всеки отделен обект). Ако има някъде нещо такова - би могло да присвоя наготово вече свършена от някой друг работа... Вакуумът ПО НИКАКЪВ НАЧИН НЕ Е празно пространство. Той е пронизан от всевъзможни полета/пространства със собствени естество/характеристики - електромагнитни, гравитационни, квантови... И по всичко изглежда (все още не го заявявам със сигурност, само подготвям почвата ), че гравитацията с нейните кривини и калибровъчните особености на електромагнетизма и квантовия свят ще наложат въвеждането и на пето и даже на повече от пет пространствени измерения в изцяло пространствената част от съответствието (може да стигнат дори до 26, както изискват някои версии на струнната теория, тъй като е желателно суперсиметрията да се избегне, а именно тя е в основата на съкращаването на броя измерения от 26 на 10, 11 или 12). Пространствено-времевата част може да си остане четиримерна (3D+1D), там евентуалните допълнителни пространствени измерения над три са представени чрез времето, кривините и калибровъчните свързаности. -
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
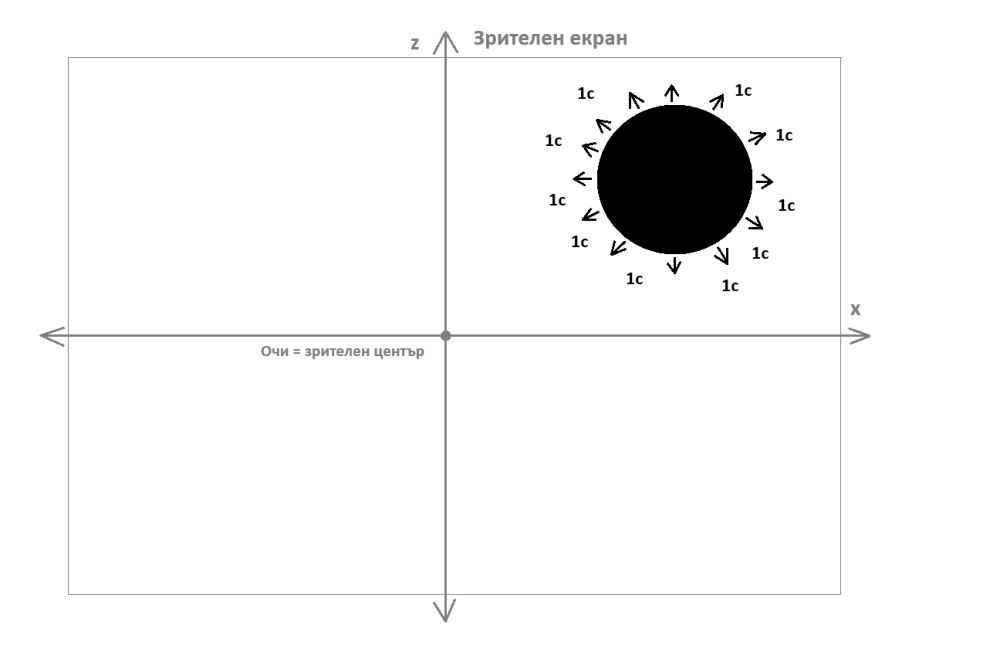
Взаимодействията, на макрониво главно електромагнитното, са основата на изграждането на физическата картина на реалността. Вкусовите, звуковите, тактилните и особено визуалните възприятия се базират основно на електромагнитното взаимодействие. Ако акцентираме на визуалното възприятие - дефинирането на някакъв обект в пространството става чрез регистрирането на излъчената или отразена от него светлина от очите ни (без очи пак е електромагнитното взаимодействие, но вече електромагнитното отблъскване на тактилното възприятие - чрез опипване да изградим някаква представа за формата и размерите на нещо в пространството). Например черният обект от изображението излъчва или отразява такъв микс от електромагнитни честоти, който изглежда като черен цвят и се регистрира от очните ретини така, че изглежда като нещо ограничено "вътре в пространството". Практически можем да приемам за "ограничен в пространството обект" каквото си поискаме и светлинните и тактилни възприятия само облекчават такива разграничения на "ограничени в пространството обекти". При вече отбелязаното от мен съответствие Симетрично (плоско) 3D+1D пространство-време/Несиметрично 4D-пространство базовите вектори на четирите пространствени координати wxyz изграждат координатната система на пространството на "наблюдателя в покой" (покоящата координатна система). Всеки един ограничен обект, който бъде дефиниран (на произволни основания) в покоящата (пространствена) координатна система е различно пространство (различна координатна система с нейния си център и с нейните си параметри на четирите координати wxyz), което различно пространство може да е неподвижно спрямо покоящата координатна система на "наблюдателя" (и така параметрите на базовите вектори на координатите на обекта ще съвпадат с параметрите на базовите вектори на координатите на "неподвижния наблюдател"), а може и да се движи (обекта, заедно с неговото пространство и заедно с неговата координатна система) спрямо координатната система на "неподвижния наблюдател" (движението може да е в границите 0с-1с) и тогава параметрите на базовите вектори на координатните системи на обекта и на "неподвижния наблюдател" ще се различават помежду си, а от там и ще се различават техните компоненти, пространствени и времеви (разликата може да се определя както чрез лоренцовите трансформации, така и чрез трансформациите на Епщайн). Знаем от лагранжовата и хамилтънова механика, че могат да се изграждат свързани с тях конфигурационно и фазово пространство. Базово, конфигурационното пространство е с три измерения, които се умножават с n-броя разглеждани обекти (така броят измерения става 3n), а фазовото пространство е с 6 измерения, които също се умножават с n-броя разглеждани обекти (така там броят измерения става 6n). По подобен начин няма проблем да се изгради четири-измерна функция, подобна на лагранжианите и хамилтънианите, чиито четири измерения да се умножават с броя обекти по подобен начин и да се получават 4n-измерения. В същността си горното произлиза от слепването на координатни парчета (координатни пространства) на 4-многообразие (и пространствено-времевото и изцяло пространственото многообразие са 4-многообразия). Именно там базовият брой измерения (в случая - четири) се умножава по броя координатни парчета, които се слепват. "Слепванията" се осъществяват чрез функции на прехода, които изразяват координатите в едно от парчетата посредством координати в другото при припокриване на такива парчета. -
В цитирания от Шпага сайт има и статия за животинското съзнание: Защо някои видове са развили съзнание, а други - не | Човекът
-
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
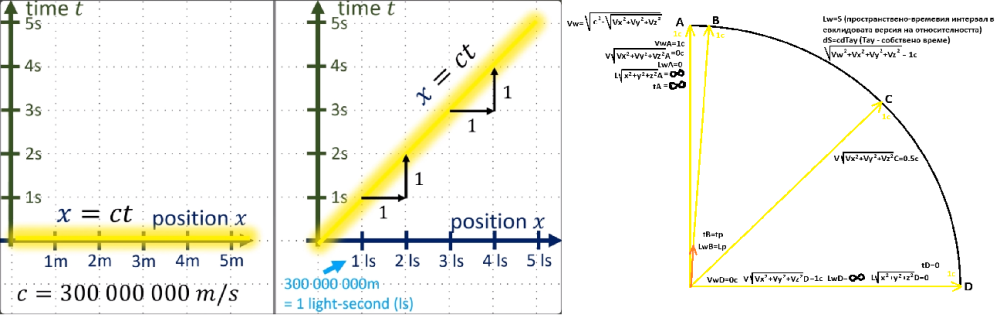
Разграничението на естеството на времето в съответствието Симетрично 3D+1D пространство-време/Несиметрично 4D-пространство като условно измерение в пространствено-времевия случай и просто като параметър на редуване на събитията в изцяло пространствения случай се представя диаграмно чрез особеността, при която в пространствено-времевия случай четвъртата непространствена координата е единствено координата на параметъра координатно време t, без нищо друго, докато в изцяло пространствения случай четвъртата координата съвместява едновременно времевия параметър Тау (собствено време), координатното време t, когато се завърти при представяне на подвижен в 3D-пространството обект и протяжността на пространството по направлението на четвъртото пространствено измерение w като базов вектор на координатата. Както скоростта се представя и извлича от наклона (ъгъла) на времевата координата в пространствено-времевите диаграми на галилеевите и лоренцовите трансформации, докато самата координата е на времето t, така и параметрите на собственото и координатното време се извличат чрез координатата на четвъртото пространствено измерение w. Бидейки дължината на параметъра w базов вектор на четвъртата пространствена координата, там са налични обичайните правила за ковариантност/контравариантност между базовия вектор и неговите компоненти (подобно на това, че колкото по-дълъг е интервалът на единица време в движеща се координатна система от гледна точка на неподвижна такава, толкова по-бавно тик-такат часовниците в подвижната от гледна точка на неподвижната система и обратното), а пък стойността на скоростовите компоненти на хиперизмерния вектор 1с по направленията на съответните измерения определя дължината на базовите вектори по координатите на съответните пространствени направления wxyz. -
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
Аз не съм имал никакъв досег с нея преди клиповете на eygenchris в Ютуб (струва ми се, че в предната тема, където пишех преди да се преместя тук, ти ми ги беше препоръчал по едно време и се оказа прав - отлично място, като цяло, не само относно линейната алгебра!) и допреди няколко месеца и не планирах да я усвоявам, даже и най-базово. Наистина не е чак толкова трудно, когато е отлично обяснено и особено, когато формираш някаква начална основа (не като мен - да не зная абсолютно нищо, но вече имам поне някакво начало).