gmladenov
Потребител-
Брой отговори
10473 -
Регистрация
-
Последен вход
-
Days Won
50
Content Type
Профили
Форуми
Библиотека
Articles
Блогове
ВСИЧКО ПУБЛИКУВАНО ОТ gmladenov
-
Откъде накъде ?!? Би ли се аргументирал какво имаш предвид. Ситуацията е по учебник.
-
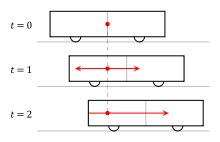
Гледам на импулса точно като на лазерен импулс - или куршум от светлина. Затова примерът няма нищо общо с аберациите. Тук имаме куршум от светлина, който се излъчва във вертикална посока. Ъгълът на излъчване/приемане на този луршум не зависи от движението.
-
Колега, казах и в другата тема: в СТО няма изискване, че движението променя ъглите на излъчване на светлината. Ако имаше такова изискване, то щеше да важи за всички лъчи светлина. Значи щеше да се знае, че ъглите на излъчване трябва да се трансформират по същия начин, както се трансформират координатите. Фактът е, че такова изискване няма. Така че нека да не си измисляме какво казва СТО, а просто да я цитираме.
-
Ситуацията е построена спрямо Втория постулат на СТО. Значи Вторият постулат твърди, че трябва да виждаме ситуацията така. Никъде в СТО не се казва, че когато светлината е излъчена от движещ се източник, трябва да променяме ъгъла на излъчване на светлината. Ако това беше така, то щеше да важи за абсолютно всички лъчи светлина, а не само за този пример. Само че в СТО няма изискване да се сменя ъгъла на светлинните лъчи.
-
Тц. Колко пъти беше обяснено, че това не е така. За пореден път: анимациите показват, че в зависимост от това кой наблюдател е избран за стационарен, ситуацията има раличен изход. Това проблемът/парадоксът тук.
-
Само ще поясня, че даденият пример няма нищо общо с аберациите.
-
Ами то е така. Тук ние просто гледаме ситуацията от два ъгъла. Това не променя как летят фотоните.
-
Не това показват анимациите. Те показват, че в зависимост от това кой наблюдател избереш за стационарен, ситуацията има различен изход. Виж горния постинг.
-
В твоя копи-пейст ти избираш стрелеца за стационарен и ни показваш какво вижда мишената от позицията на подвижна. Само че анимациите показват нещо друго. Стандартният начин да се раглеждат системите в СТО е следния: Избираме една система за стационарна Прилагаме Лоренцовата трансформация Гледаме как координатите са транслирани в подвижната система Значи като цяло гледаме "стационарна -> подвижна" системи. Това, което аз показвам, е друго: Избираме едната система за стационарна Изибираме другата система за стационарна Сравняваме двете стационарни системи Значи тук сравнението е "стационарна към стационарна" системи, а не "стационарна -> подвижна" системи (което ти показваш). Погледнато по друг начин: Нека ти и Скенер да решавате задачата. Ти избираш стерелеца за стационарен, а Скенер избира мишената за стационарна. След това сравняваме двете решения и какво се оказва: в твоята стационарна система импулсът не уцелва мишената в неговата стационарна система импулсът уцелва мишената Извод: в зависимост от това кой наблюдател сме избрали за стационарен, ситуацията има различен изход (завършва по различен начин). Това е парадоксът тук и това показват анимациите. А в твоя копи-пейст ти избираш стрелеца за стационарен и ни показваш какво вижда мишената от позицията на подвижна ... и това правилно си го показала. Само че ти по никакъв начин не решаваш парадокса: защо ситуацията има различен изход в зависимост от това кой наблюдател сме избрали за стационарен? Ти на този въпрос не си отговорила - а и не можеш да отговориш, защото според СТО така стоят нещата. Именно това е парадоксът. Ето сега един копи-пейст и от мен. Той е от първоначалния постинг: Принципното последствие тук е, че траекторията на светлинен импулс между две тела не можеда бъде изчислена правилно ако не знаем кое от тях е в покой и кое се движи. Така че постановката на Релативизма, че всяко тяло може да бъде произволно избрано както застационарно, така и за подвижно, в същност не работи в реалността. Щом не можем да определим състоянието на движение на две тела, значи няма как да изчислим и траекторията на светлинен импулс между тях.
-
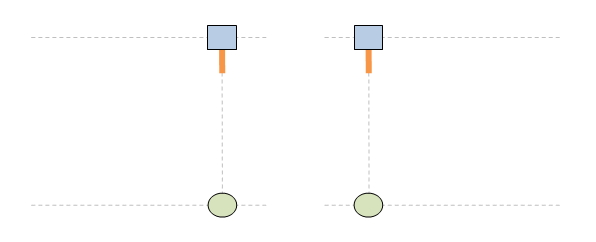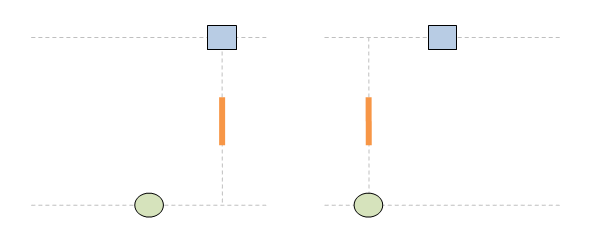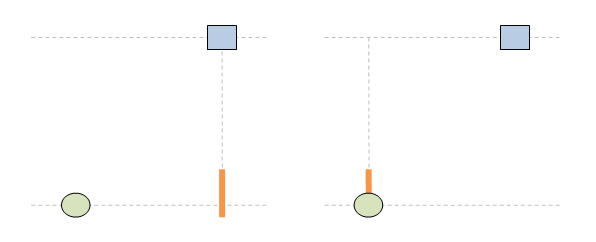
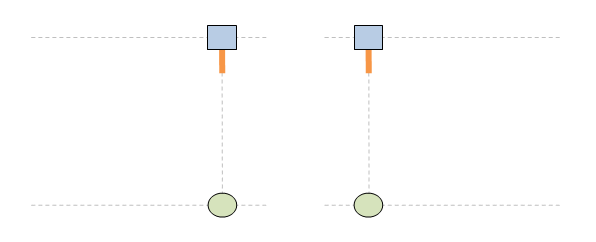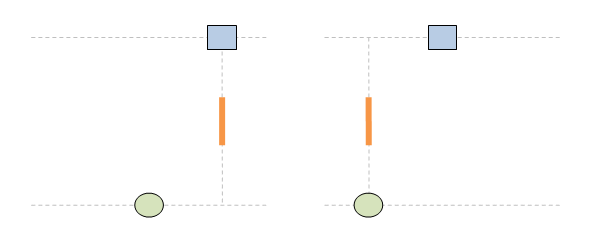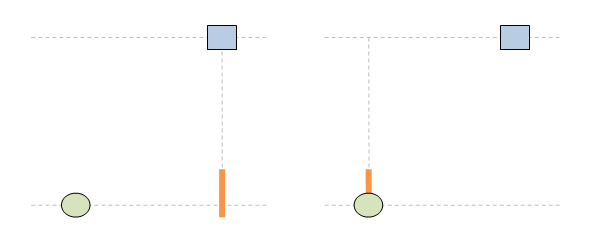
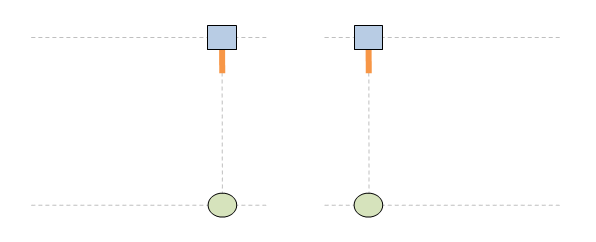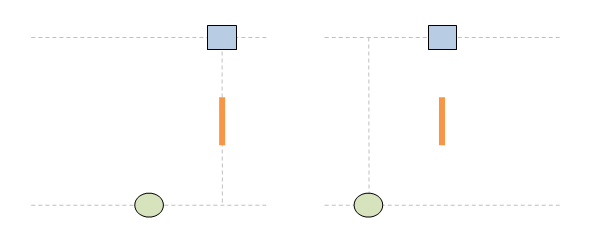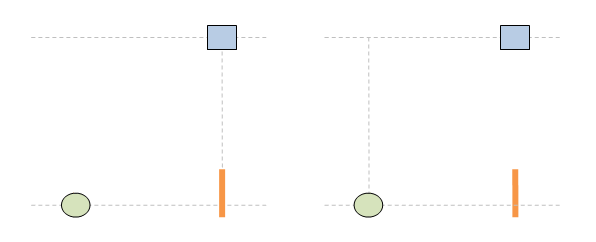
Чети целия постулат. Аз ти гововоря за втората част: ... no matter how fast the source of light and the observer are moving relative to one another. На български: ... без значение колко бързо се движат източникът на светлина и наблюдателят един спрямо друг. Или казано по същество: скоростта на светлината не се влияе от движението на източника. Това виждаме и в анимацията. В ляво източникът е стационарен, а в дясно той се движи. Но и в двата случая скоростта на светлината е еднаква: тя е с. Освен това и в двата случая импулсът е излъчен в точка (х=х'=0) и е е излъчен вертикално и в двете системи. Като се съберат всички тези факти в едно, пътят на светлината излиза еднакъв и в двете отправни системи. В същото време позицията на мишената е различна, тъй като в едната система тя е стационарна, а в другата тя е подвижна. Така се завършва светлината да има еднакъв път и в двете системи, а мишената да се намира на различни места.
-
Аз съм ти го подчертал да го видиш, а ти казваш, че не е така. Добре. Ето ти и цитат, за да видиш, че не си измислям: Эйнштейн положил в основу теории относительности постулат о независимости скорости света в вакууме от движения источника. Независимостта на светлината от движението на източника е принципно положение в СТО.
-
Посоката няма значение. Важното е, че според Втория постулат на СТО светлината винаги е изотропна спрямо наблюдателя. Ами защото ... по дефиниция ... светлината е независима от източника. Ето го втория постулат: Всеки лъч светлина се движи в "стационарната" координатна система с установената скорост с, независимо дали лъчът е излъчен от стационарно или движещо се тяло. Пътят на светлината е еднакъв и на двете анимации горе, защото няма никакво значение дали стрелецът се движи или не. Така казва Вторият постулат.
-
Виж ми поправения постинг. Точно за джама добавих.
-
Няма значение от какво са стените. Важното е дали имаме отворено или затворено пространство. Затвореното пространство пренася/увлича светлината. Това е принципът. Като се движиш в кола или влак и отвориш прозореца почва да духа. А когато го затвориш спира да духа. Духа ли по-малко ако стените са от картон вместо от стомана?
-
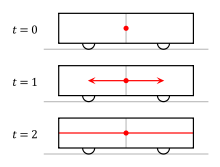
Вторият постулат постулира, че скоростта на светлината е изотропна във всички отправни системи (изотропна = еднаква във всички посоки). Ето известният пример с влака и гарата, който илюстрира тази постановка. Наблюдател във вагона: скоростта на светлината е изотропна спрямо него: Наблюдател на гарата: скоростта на светлината е изотропна и спрямо него: Значи според СТО светлината винаги е изотропна спрямо наблюдателя. Така постулира Втория постулат. Тук пътят на светлината също е еднакъв в двете отправни системи: еднакъв спрямо системата ... но различен спрямо вагона. В горните анимации е абсолютно същото: едакъв спрямо системата ... но различен спрямо мишената. Паралелът между двата примера е очевиден.
-
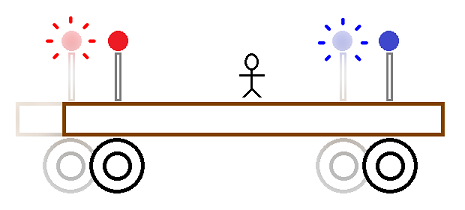
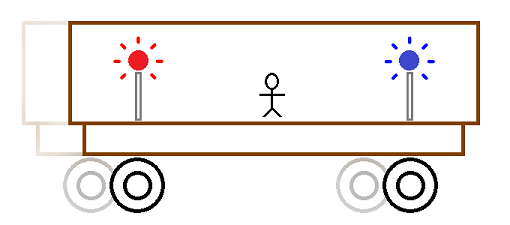
Разликата вън/вътре се определя от преносимостта на светлината. Подвижен вагон с две крушки в левия и десния край на вагона. Двете крушки светват едновременно, но заради движението на вагона синята светлина изминава по-къс път докато стигне до наблюдателя и достига до него първа. Червената светлина изминава по-дълъг път и достига втора до наблюдателя. В този случай вагонът и светлината се движат в едно и също пространство. Тук нямаме преносимост на светлината. Същият пример, но със затворен вагон. Тук вече имаме преносимост на светлината. Затвореното пространство на вагона пренася/увлича светлината със себе си. Съответно синята и червената светлини достигат едновременно до наблюдателя.
-
Ами точно затова имаме парадокс !! Ти дефакто ми обясняваш защо имаме парадокс ... и си абсолютно прав. ЛЯВО: стрелецът е стационарен. ДЯСНО: мишената е стационарна. И в двата случая пътят на светлината е еднакъв, както се вижда на анимацията. Така повелява Вторият постулат. Различното е двете системи е, че мишената в едната се движи, а в другата не. Това води до парадокса: еднакъв път на светлината + различни позиции на мишената => парадокс Ако сега погледнем другата анимация, светлината има различни пътища в двете системи: различен път на светлината + различни позиции на мишената => няма парадокс
-
Вервай, батка, вервай. Щом те влече.
-
Опитната постановка трябва да се намира в движение спрямо средата, в която се разпространяват светлинните вълни. Иначе как ще измери различни скорости в различните посоки. Ако опитът на ММ се проведе в открития космос, тогава той ще даде положителен резултат (стига пътят на светлината също да преминава през открития космос). Ако повторят опита на ММ вътре в МКС, той ествествено пак ще даде нулев резултат.
-
Добре, обясни по-подробно примера с луната, за да видя какво имаш предвид. Според теб аз къде бъркам.
-
Нещо друго, което забравих. Математиката на СТО работи, защото приемаме за нормално съкращението на дължините и забавянето на времето. Но ако кажем, че това не са нормални "явления", математиката веднага спира да работи. Съкращение на дължините никога не е наблюдавано, а експериментите, които уж показват забавяне на времето (като този с мюоните) са меко казано трагични. Така че парадоксът в математическата логика на СТО е съвсем реален. Просто е прието той да не се смята за парадокс.
-
Вече ти отговорих: няма да губя време за тези въпроси. Що ти не направиш някоя анимация и да ни покажеш.
-
Това е скоростта на спътнците в космическото пространство ... а не спрямо нещо. Знам, че си свикнал движението да е спрямо нещо ... но това в същност не е задължително. Абсолютното движение, например, не изисква отправна точка. Ако толкова държиш, движението е спрямо вакуума на космоса. Но не ми казвай, че такова движение няма. Ограничението всичко да е "спрямо" е ограничение на доктрината на релативизма, а не закон на физиката. Ако бъркаш доктрина със закон на физиката, явно имаш още да учиш.
-
Не, батка. СТО е математически-вярно описание на несъщестуващо явление: еднаква скорост на светлината за всички наблюдатели. Представи си теория за гравитацията, в която се приема, че гравитацията е отблъскваща, а не привличаща. Със сигурност ще докараш математиката да работи ... но от това тази теория няма излезе вярна. Същото със СТО. Математическа грешка в теорията няма. Но цялата теория е основана въру погрешно допускане. Така че наистина успех, ако търсим грешка в математиката. Няма спор. Грешката на СТО е в това, че тя не отговаря на реалността. Това показват горните анимации.
-
Там е друго: пътят на светлината е различен по перпендикулярните рамена. В тукашния парадокс има само една рамо вертикално надолу. И това рами го гледаме един път отгоре надолу и втори път от долу нагоре. Тук светлината няма различен път. Имаме само различна перспектива.