gmladenov
Потребител-
Брой отговори
10473 -
Регистрация
-
Последен вход
-
Days Won
50
Content Type
Профили
Форуми
Библиотека
Articles
Блогове
ВСИЧКО ПУБЛИКУВАНО ОТ gmladenov
-
За пореден път: първо избирам единия наблюдател за стационарен, а след това другия. Според СТО и релатвизма няма значение кой наблюдател съм избрал за стационарем. Аз се възползвам от това право и сравнявам какво се получава ако всеки един от тях е избран за стационарен. Сега ти нова песен запя: че това били две отделни ситуации. Е да, ама не. Ще ви изчакам да вденете. Споко, не бързайте.
-
Тц. Първо показвам ситуацията от едната гледна точка, а след това от другата. Значи имаме една и съща ситуация от две гледни точки. Въобще не са две ситуации.
-
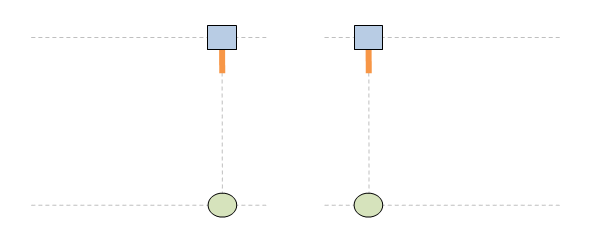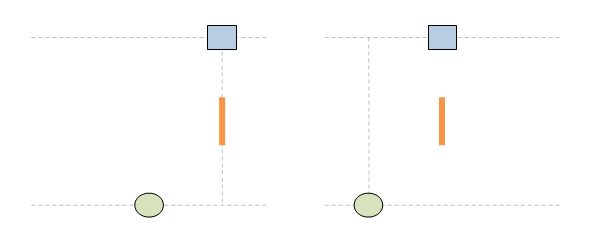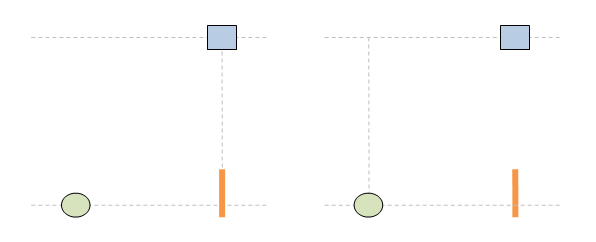
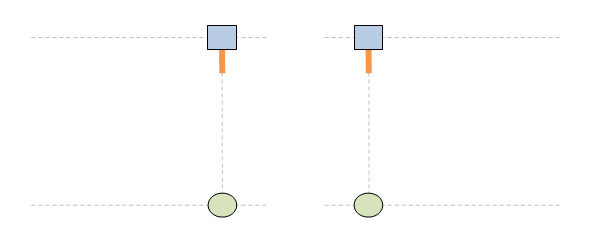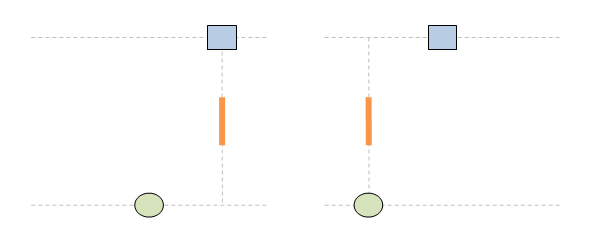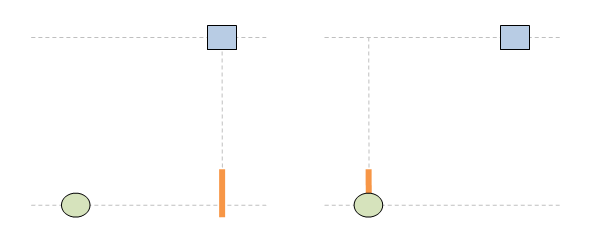
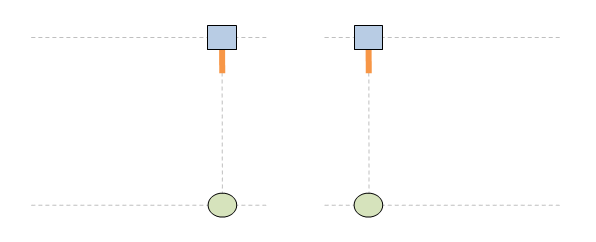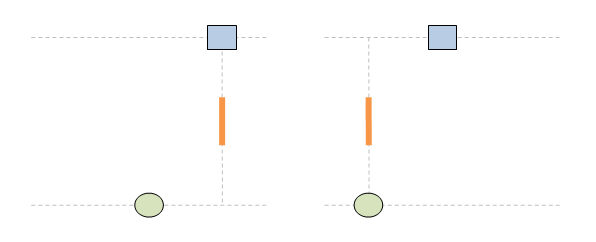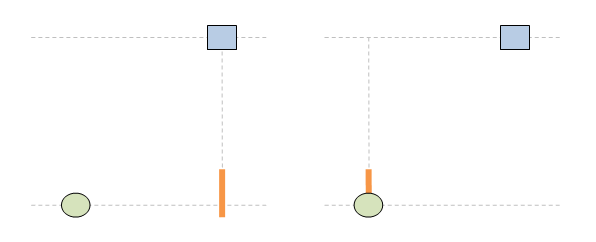
Нека пак да сложа анимациите, за да не са забравя за какво е тази тема. 1. Ако светлината имаше инерция, ролите на стационарен и подвижен наблюдатели са симетрични и няма никакво значение кой наблюдател е избран за стационарен и кой за подвижен. Симетрията на наблюдателните роли е фундаментален принцип на Релативизма: 2. Светлината, обаче, няма инерция. По тази причнина траектороията на светлината е различна в зависимост от това кой наблюдател се води за стационарен и кой за подвижен. Това нарушава базовия принцип на Релативизма за симетричност на наблюдателните роли. Извод: принципът на Релативизма за симетричност на наблюдателните роли е несъвместим с постоянството на скоростта на светлината. Това е теоретичен проблем за Релативизма. Релативизмът работи само за механичо движение и е принципно несъвместим с движението на светлината.
-
ОК. Явно не сме дорасли за смислени дискусии. А за религиозни дискусии днес нямам време.
-
Не съм съгласен. Никой досега не е оборил парадокса без да въведе разлики в двете системи. Единствената разлика между двете системи е в това кой се смята за подвижен и кой за стационарен. Друга разлика няма.
-
Не забравай парадокса, за който е отворена темата. Въпреки всичките ти протести, ти не си показал никакъв смислен аргумент срещу него. Направи работеща анимация, която го оборва, и тогава ще говорим. Засега нищо не предлагаш освен празна реторика.
-
Хубаво. Предположение ... но го сложи наравно с базовото допускане на СТО: скоростта на светлината е еднаква за всички (СТО) светлината е преносима и така създава илюзията, че скоростта на светлината е еднаква за всички Всички опити, които оборват етърната теория, също така показват, че светлината е преносима. Много е изкушително да си помислим, че тези опити също показват, че скоростта на светлината е еднаква за всички. Само че как да обясним диполната анизотропия. В същото време ако се приеме, че светлината е преносима, всички парадокси на СТО изчезват, както и скъсяването на дължините и забавянето на времето.
-
Гравитацията аз я пренебрегвам. Тя със сигурност оказва влияние, но слабата гравитация може да се пренебрегне.
-
И по-конкретно? Кой, кога и къде го е проверявал? Статии в сериозни списания? Най-красноречивият опит от всички: обсерваторията за гравитационни вълни ЛИГО. Тя представлява един гигантски интереферометър, който от 2002г насам ежесекундно показва, че светлинната вътре във вакуумираните тунели на обсерваторията остава изотропна докато тези тунели се движат из космоса ... с 370 км/с. Тоест, ЛИГО показва, че тунелите на обсверваторията пренасят/увличат със себе си светлинните вълни, разпространяващи се вътре в тях. За да разбере преносимостта на светлината, обаче, човек първо трябва да се запита дали светлинните вълни наистина са преносими и какво ни дава основание да смятаме така. Значи първата стъпка е да допусне ... хипотетичната ... възможност, че СТО може би има неправилна представа за това как се разпространява светлината. Но ако човек предпочита да не си задава въпроси ... а само да рецитира евангелието буква по буква ... няма как да разбере преносимостта на светлината. Защото в евангелието наистина не пише, че светлината е преносима. Потвърждавам. За да разбере истината, човек трябва да погледне извън евангелието. Така че моля не ми цитирайте евангелието. Всички знаем какво пише в него.
-
Вакуумът в затворено пространство също увлича. Безброй опити го доказват. Разбира се трябва акъл и мислене, за да се разберат тези неща. Една закостеняла консерва естветвено няма как да ги разбере. Ама какво да я правиш. Тя толкова си може.
-
За мен хипотезите са измислици, така че грамофонната плоча в моята глава е въображаема. Според теб, обаче, хипотезите не са измислици. Следователно, хипотетичното ако в глава ти никак не е въображаемо, а съвсем истиско. С това съм напълно съгласен.
-
ОК. Аз имам научна хипотеза, че ти в главата имаш ако. И тъй като това е научна хипотеза - а не някаква моя приумица - значи е абсолютен факт, че ти в главата имаш ако.
-
Показваш, че ти липсва логическо мислене. Стига суеверия, а направи логическите връзки: ако тогава са смятали, че има етър ... а такъв не съществува ... значи етърът е въображаем ако тогава са смятали, че има етър ... и той съществува ... значи етърът съществува и до днес Ако хипотезата за съществуването на етъра не се потвърждава, значи тази хипотеза е просто измислица, приумуца, хрумка, "що па не" и т.н.. Мястото на непотвърдените хипотези е на боклука на историята.
-
Да, това е така. Проблемът е, че движението на земята в етъра е неоткриваемо ... но само от опити, извършени вътре в атмосферата. Веднъж като са направят измервания извън атмосферата, това движение веднага се открива: диполната анизотропия. Значи допускането на СТО, че движението на земята в етъра е неоткриваемо, се основава на половинчати експериментални данни. ("Половинчати" в случая означава, че ако е трябвало да се направят измервания вътре и извън атмосферата, само първата половина от тези измервания са направени.)
-
Абсолютно вярно ... ако имахме някакви доказателства за съществуването на етъра. Без такива доказателства излиза, че "движението в несъществуващия/въображаем етър е неоткриваемо". Или по-общо поставено: няма експеримент, който да открие движението на еднорог във вечните ловни полета.
-
Друго уточниение: първоначална хипотеза = резонно предположение, базира се на логика вече-опровергана хипотеза = очевидно, че е просто приумица/измислица
-
Като се говори за етър е важно да се направят следните логически връзки: ако тогава са смятали, че има етър ... а такъв не съществува ... значи етърът е въображаем ако тогава са смятали, че има етър ... и той съществува ... значи етърът съществува и до днес Това е много важно да се уточни: или светлоносещият етър е въображаем и никога не е съществувал ... или той съществува и до днес. Това е така, защото ако на светлината наистина и трябва етър за разпространение, този етър трябва да съществува и днес. Не може някога да е имало етър, а днес вече не. Нали на днешната светлината също и трябва етър за разпространение. Ако пък на светлината не и трябва светлоносещ етър, значи той винаги е бил въображаем (или илюзорен, измислен, приказен и т.н.) (Тези съждения важат само за светлоносещия етър, не за други видове етър.)
-
Да, ако скъсяването беше истинско, оипитът на ММ нямаше да го хване. Само че тази идея със скъсяването е много съмнителна. Пак да кажа: опитът на ММ показва пълно увличане/пренасяне на светлината от атмосферата. Само че физиците на времето са били абсолютно убедени, че атмосферата не увлича светлината. От там идва объркването. Иначе нулевият резултат е очакваният резултат. Няма никаква мистика в него.
-
Според замисъла на опита, пътят на светлината успоредно на движението е по-дълъг отколкото напречно на движението. Значи на светлината ще и отнеме повече време да измине успоредния път отколкото напречния път. Интерферометърът е достатъчно чувствителен да хване тази разлика. Чел съм хора да се захващат за това, че опитът на ММ мери двупосочна скорост на светлината, а не еднопосочна. Не е това проблемът, обаче. Проблемът е увличането на светлината от атмосферата.
-
Скенер и затова е прав. Прецизността на опита на ММ е много висока, а апаратът (интерферометър) като цяло е голямо изобретение. Дали са му Нобелова награда на Майкелсон за апарата и не са сгрешили.
-
Нищо не доказва, защото вакуумът в затворени пространства също "увлича". Ти това не разбираш ... а наблюдението показва точно това. Но напълно се съгласявам, че е излишно да спорим.
-
Тц. В литературата навсякъде пише, че опитът на ММ указва пълно увличане на светлината. Само че достатъчно други опити (уж) оборват идеята за увличането. Затова нулевият резултат на ММ не се тълкува като увличане. А проблемът в същност е неразбиране на това как работи "увличането" на светлината и най-вече идеята, че увличането на светлината от въздуха е пренебрежимо малко.
-
Да, но скоростта на вятъра е толкова малка в сравнение със скоростта на светлината, че изместването е незабележимо. Ето нещо по-забележимо: пречупване (рефракция) на светлината от въздуха: