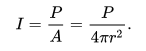gmladenov
Потребител-
Брой отговори
10473 -
Регистрация
-
Последен вход
-
Days Won
50
Content Type
Профили
Форуми
Библиотека
Articles
Блогове
ВСИЧКО ПУБЛИКУВАНО ОТ gmladenov
-
Тц. Според класическата физика светлината е преносима и достига едновременно до двете стени на вагона и за двата наблюдателя. Така че в класическата физика няма никакъв парадокс. Интензитетът на светлината е еднакъв въс всички отправни системи. Естествено в класическата физика скоростта на светлината не е еднаква за всички наблдатели, а е относителна.
-
Хехе, тоагава за каква относителност на едновременността бленува СТО ?? Щом интензитетът в двата края на вагона е еднакъв, значи светлината е изминала еднакъв път до тях ... и пристига там едновременно и за двата наблюдателя. Значи няма относителност на едновременността. Няма две добри, колега. Ти нещо се обърка май.
-
Точно като в примера, който съм дал. Благодаря за потвърждението.
-
Явно дори не си прочел за какво става дума. Няма лошо. Не е важно да разбираш за какво се говори. Важното е да участваш.
-
Да, но нали по условие говорим за видима светлина и стените на вагона са непрозрачни. Тогава как светлина, излъчена вътре във вагона, ще достигне до датчиците отвън ?? Освен това дори са отвън, датчиците пак ще се намират в отправната система на подвижния наблюдател. Значи наблюдетля на гарата - който е стационарен - пак не може да направи измерване.
-
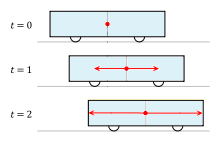
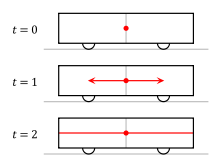
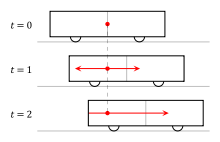
Здравейте, В тази тема ще изложа един от неразрешимите парадокси на Специалната Теория на Относителността (СТО), който аз наричам "парадоксът на светлинния интензитет". Той се базира на известния пример с влака и гарата, който обичайно се дава за илюстриране на концепцията за относителност на едновременността. Условието на примера е както следва: Влак и гара се намират в относително движение. В момента когато наблюдател на гарата се изравнява с наблюдател във влака, вътре във влака светва крушка. В задачата се търски как всеки от двата наблюдателя вижда светлината от тази крушка. Според наблюдателя във влака, гарата е тази, която се движи, докато влакът е в покой. Така спред този наблюдател светлината от крушката достига едновременно до лявата и дясната стени на вагона, както е показано на следната картинка: Според наблюдателя на гарата, обаче, влакът е този, който се движи, а гарата е в покой. По тази причина светлината от крушката достига първо до лявата стена на вагона, и след това до дясната; тоест неедновременно: Разликата между гледните точки на двата наблюдателя се обяснява с концепцията на СТО за относителност на едновременността: събития, които са едновременни за един наблюдател са неедновременни за друг. Хубаво, но относителността на едновременността има и едно друго последствие. Както се вижда на втората картинка, светлината достига неедновременно до двете стени на вагона защото тя изминава различен път: нейният път до лявата стена на вагона е по-къс отколкото този до дясната. Проблемът е, че по закона за обратните квадрати, интензитетът на светлината е обратно-пропорционален на изминатия от светлината път: Така се стига до следния парадокс: Според наблюдателя вътре във влака, светлината изминава еднакъв път до двете стени на вагона. Следователно, нейният интензитет при стените на вагона ще бъде еднакъв. Според наблюдателя на гарата, обаче, светлината изминава различен път до двете стени на вагона. Следователно, нейният интензитет при стените на вагона ще бъде различен. С други думи, относителността на едновременността в горния пример неизбежно води до различен интензитет на светлината при двете стени на вагона. И наистина, щом разликата в пътя на светлината причинява относителност на едновременността, същата тази разлика ще причини и различен интензитет на светлината при двете стени на вагона. Това е неизбежно. Защо това е неразрешим парадокс? Първо, според СТО излиза, че интензитетът на светлината не е обективно свойство на светлината, а субективно "виждане" на наблюдателя. Инензитетът на светлината в горния пример няма обективна стойност, а е различен за различните наблюдатели. Втората причина е още по-интересна и е свързана с измерването на интензитета на светлината. Нека се ограничим само със светлината от видимия спектър, която не може да преминава през непрозрачни материали. Ако стените на вагона са непрозрачни, никаква видима светлина, излъчена вътре във вагона, не може да го напусне. Следователно, само вътрешният наблюдател може да направи физически измервания на интензитета на тази светлина. Външният наблюдател, от друга страна, няма достъп до светлината вътре във вагона и няма как да извърши физическа измервание на нейния интензитет. Това означава, че само "виждането" на вътрешния наблюдател е обезпечено с физическо измерване, докато "виждането" на външния наблюдател не е. Във физиката водещи са измерванията, така че "виждането" на външния наблюдател в същност е невалидно. То дефакто е една произволна хрумка, която няма как да се защити с физически измервания, защото това е физически невъзможно. Извод Посоченият парадокс показва две неща. Първо, според СТО излиза, че интензитетът на светлината не е обективно свойство на светлината, а субективно "виждане" на наблюдателя. Както посочихме, обаче, не всички наблюдатели могат да защитят своите "виждания" с физически измервания, така че те в същност са невалидни. В горния пример външният наблюдател няма как да измери интензитетът на светлината вътре във вагона, защото тя е физически недостъпна за него. Така че неговото "виждане", че интензитетът на тази светлина е различен при двете стени на вагона, е просто една произволна хрумка, която по никакъв начин не може да се защити с физическо измерване. Изводът от всичко това е, че СТО приема за истина "виждания", които противоречат на физическите измервания. Благодаря за вниманието.
-
Ами виж, че за механично движение нещата излизат както се очаква (според СТО) - а за светлината не излизат. Парадоксът е съвсем истински. Няма объркване тук.
-
Дорис, много съм ти задължен за снизходителното поучение. Само ще поясня, че парадоксът се получава за светлината - но изчезва ако погледнем механично движение. В този случай няма никакви значение кой наблюдател сме избрали за стационартен и кой за подвижен ... точно както релативизма казва и както е показано на следната анимация.
-
Това ми показва, че не си вникнала в парадокса. Обясних подробно какъв е проблемът с твоята анимация - но ти явно или не си прочела обяснението, или пък не те интересува да вникнеш. Парадоксът е много прост за тези, които имат желание да го разберат. Позицията на останалите е ясна.
-
... или СТО бърка кардинално. Написал съм сума обяснения, приложил съм картинки и анимации ... и всички те покзазват едно и също нещо: избираш единия наблюдател за стационарен - става едно избираш другия за стационарен - става друго Направи си труда да вникнеш в парадокса и ми посочи грешката.
-
Лапландец, не ми се спори ... но не си прав.
-
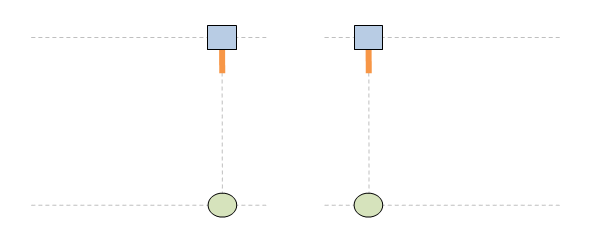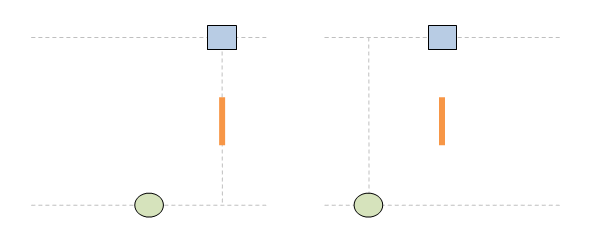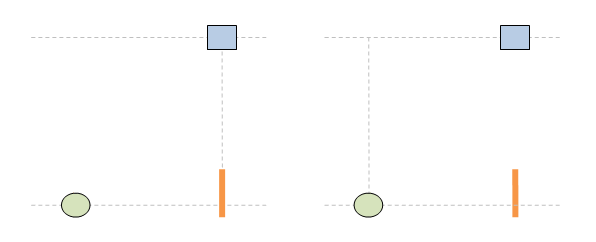
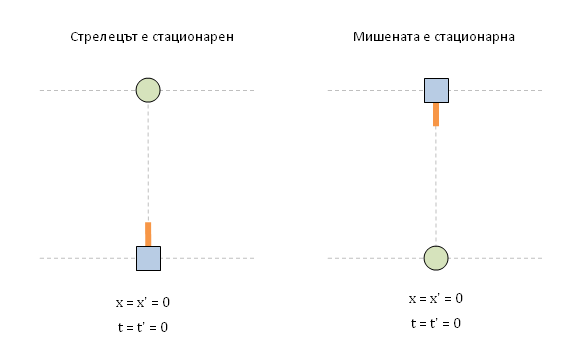
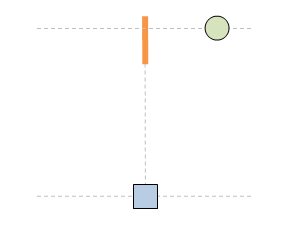
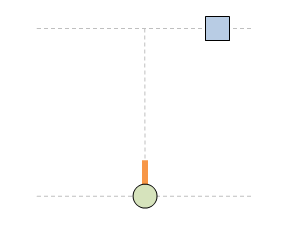
Ето пак примера, този път с нови картинки. Имаме два наблюдателя - стрелец и мишена - които се намират в относително движение един спрямо друг. Съгласно правилата на СТО и релативизма, всеки един от тях може да бъде избран както за стационарен, така и за подвижен. Иначе казано, наблюдателните роли стационарен и подвижен са взаимозаменяеми и произволно-избираеми. Така в нашият пример можем да изберем както стрелецът за стационарен, така и мишената. Няма ограничение. Нека началата на двете отправни системи съвпадат в момент t=t'=0 и точка x=x'=0. В този момент стрелецът изстрелава лазерен импулс перпедникулярно на движението. Тоест, вертикално по оста у. В зависимост от това кой от двата наблюдателя изберем за стационарен, двете системи са огладелно отражения една на друга: Нека първо погледнем отправната систена на стационарния стрелец. В момент t=2 в тази система, лазерният импулс вече е изминал разстоянието у между стрелецът и мишената. За това време, обаче, тя вече се е преместила надясно и импулсът не я уцелва: Значи ако изберем стрелецът за стационарен, тогава лазерният импулс не уцелва мишената, защо тя е подвижна. За времето, за което импулсът би я достигнал, тя се е преместила надясно и така той не я уцелва. Нека сега видим какво се получава ако сме избрали мишената за стационарна: В този случай срелецеът е този, който се движи, докато мишената не се мести и съответно той я уцелва. Значи като цяло единственето нещо, което направихме тук, е да сменим кой от двата наблюдателя е стационарният: стрелецът или мишената. И както се вижда, в зависимост от това кой от тях е избран за стационарен, имаме два различни изхода на ситуацията: в единия случай импулсът уцелва мишената, докато в другия той не я уцелва. Това, разбира се, е физически невъзможно - и точно затова имаме парадокс. Не може изборът на наблюдателна роля да променя какво се случва. Не работят така нещата.
-
Вие сте идентични с двата "вътрешни" наблюдателя. Все едно вие се тях: ти си стрелеца, а Скенер е мишената. Значи вие не сте трети и четвърти наблюдатели, а първи и втори.
-
Забрави за трети наблюдател, колега. Няма такъв. Ти избираш стрелеца за стационарен, а Скенр избира мишената. Къде виждаш трети наблюдател тук?
-
Спред СТО и релативизма, ролите на стационарен и подвижен наблщдатели са взаимозаменяеми и произволно-избираеми. Имаме право да изберем както единия наблюдател за стационарен, така и другия; това са два еднакво-валидни избора. Казано по друг начин: Представи си, че ти и Скенер решавате задачата. Ти избираш стрелеца за стационарен, а Скенер избира мишената за стационарна. След това отговаряте на въпроса: лазерният импулс уцелва ли ракетата или не? Твоято отговор ще бъде "не, не я уцелва", а отговорът на Скенер ще бъде "да, уцелва я". Въпросът е, защо вашите отговори се различават. Това е парадоксът.
-
Колега, тук сме наши хора и се знаем. Но извън форума не я казвай тази глупост. За теб е по-добре.
-
Не ти разбирам мисълта. Повтарям мантрата до връсваяне, защото след 600+ коментара, никой от релативистите все още не е анализирал/коментирал това, за което е парадокса. Защо ти първо не избереш единият наблюдател за стационарен и да покажеш той какво вижда в собствената си (стационарна) система. След това да избереш другия наблюдател за стационарен и за него също да покажеш какво той вижда в собствената си (стационарна) система. Никой от релативистите не е направил това упражнение. А вече ми е втръснало да повтарям, че точно това трябва да се направи, за да се види парадокса.
-
Да. Когато началата на двете системи съвпадат, както х=х'=0, така и t=t'=0. Без тази обща точка във времето и пространството, всяко сравнение между двете системи би било невъзможно. Дефакто това е базата за сравнение.
-
Да не забравяме официалната мантра на този парадокс: избираш единия наблюдател за стационарен - става едно избираш другия за стационарен - става друго За това иде реч.
-
Редактирах си предишния коментар, защото се обърках. Извинявам се. Според СТО подвижни обекти нямат общо време, а не пространствено отдалечени.
-
СТО не твърди това. Тя твърди, че подвижни обекти нямат общо време, а не пространствено отдалечени обекти. Ако два обекта са неподвижни един спрямо друг, тяхното време ще е общо дори те да се намират на светлинни години разстояние един от друг. В момента, обаче, в който те почнат да се движат един спрямо друг, те вече не са на едно време. Така е според СТО.
-
Ако си дадеш труда да вникнеш в парадокса, може би ще го разбереш.
-
Благодарение на доброжелателните коментари на нашите приятели релативисти, избирам следната фраза за официална мантра и мото на посочения парадокс: избираш единия наблюдател за стационарен - става едно избираш другия за стационарен - става друго Като всяка мантра, и тази ще се чува често.
-
Да, прав си ... но аз не това показвам. Аз показвам, че: избираш единия наблюдател за стационарен - става едно избираш другия за стационарен - става друго За да го покажа това, аз неизбежно показвам кой какво вижда в своята стационарна система. Така се завършва да сравняваме две стационарни системи, а не стационарна -> подвижна, както е обичая. Хиляда пъти го повторих това и още ще повтарям, щом трябва (явно).
-
Сменя се ако гледаш стационарна -> подвижна система. Само че аз не показвам това. Ще повтарям толкова пъти, колкото трябва. Парадоксът се състои в следното: избираш единия наблюдател за стационарен - става едно избираш другия за стационарен - става друго