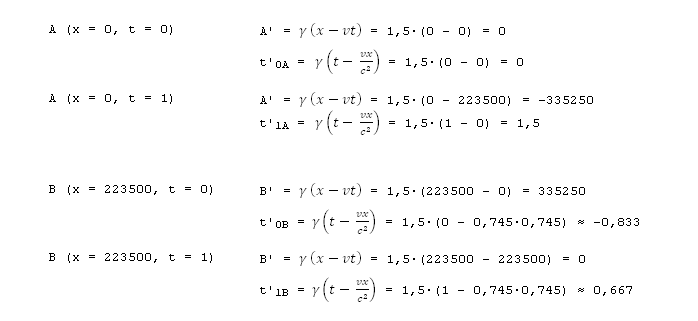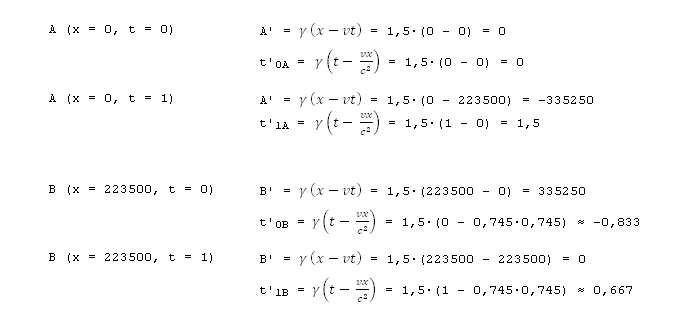gmladenov
Потребител-
Брой отговори
10473 -
Регистрация
-
Последен вход
-
Days Won
50
Content Type
Профили
Форуми
Библиотека
Articles
Блогове
ВСИЧКО ПУБЛИКУВАНО ОТ gmladenov
-
Доказателство, което не подлежи на никакво съмнение. Реликтовото излъчване, например, се смята за доказателство в подкрепа на теорията за Големия Взрив. Ако то беше абсолютно доказателство, значи теорията за ГВ би трябвало да е абсолютно вярна и да не може да се поставя под съмнение. Това дали е така??
-
Критерият дали една физическа теория е вярана или не е дали тя отговаря на действителността. Експерименталните доказателства целят да проверят точно това, но тълкуването на експерименталните резултати не е абсолютно. Така че дори на експериментите не може да им се има пълна вяра. Какъв ти е опита с интуицията в програмирането ??
-
Щеше да си прав ... ако доказателствата/фактите бяха абсолютни. Идеята на СТО за относителност на едновременността почива на "факта", че скоростта на светлината остава постоянна дори когато се движиш. Аз лично не мисля, че това е факт, докато някои наистина го смятат за факт. Също така попитай плоскоземците дали има такъв факт, че земята е кръгла?? В крайна сметка всичко е въпрос на вяра ... включително дали нещо е факт/доказателство или не е.
-
Мир на праха му!
- 2 мнения
-
- 3
-

-
Напротив. Един по един откривам триковете на СТО, с които тя мъти водата. В предишна тема открих, че СТО разрешава ясновидството. Както се оказа, обаче, това бил известният парадокс на Андромеда. Единственото странно нещо в случая е, защо никой няма проблем с него. Дефакто ясновидството се приема за нормално. Същата работа и със сегашната тема. СТО "тайно" надува скоростите в движещата се отправна система, но и това не се смята за проблем. Просто "компенсираме" - и хоп, всичко е точно. А това, че СТО прави времето на салата, няма никакво значение. В крайна сметка, обаче, СТО е грешна и рано или късно ще и хванем цаката. Борбата продължава .
-
Прочел съм, но не се съгласявам. Ето какво си написал: В твоят случай трябва да компенсираме преместването ... 335250 + (-0.833*223500) = 149000 км - разстояние между точките А' и В' определено в един и същи момента t'=0. Работата е там, че ти използваш скоростта v = 223500, което е скоростта в земната отправна система, а не скоростта в движещата се отправна система ... която не е същата. А това, което аз показвам, е че СТО върти двойно счетоводство. СТО надува както разстоянията в движещата се отправна система, така и скоростите. След което прави трикове с времето, за да натамани сметките. И ако "официалната" скорост на движение е v, то същинстала скорост v' е по-висока от v, което се вижда от графиката. Само че моят пример си загубва смисъла, щом не е ясен. Явно двойното счетоводство не е толокова видно. Карай да върви.
-
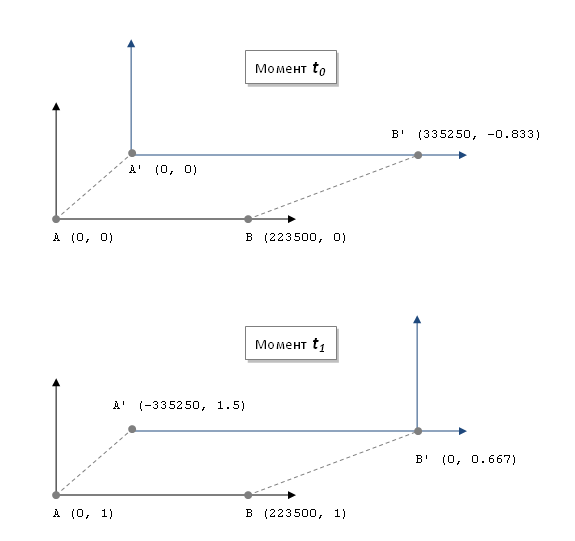
Ето я пак картинката на движението, но този път с всички координати (пространствени + времеви): Координатите А' и В' са сметнати с правата Лоренцова трансформация за моментите t0 и t1. Тъй като имаме две точки (А и В) и две времена (0 и 1), завършваме със следните трансформации: в момент t0 превеждаме А(0, 0) -> А' (0,0) и В(223500, 0) -> В'(335250, -0.833) в момент t1 превеждаме А(0, 1) -> А' (-335250, 1.5) и В(223500, 1) -> В'(0, 0.667) Ето пак таблицата с изчисленията. Движението в земната отправна система е от точка А в момент t0 до точка В в момент t1. Тоест, от А(0,0) до В(223500, 1). Въпросът е как изчисляваме същото това движение в ракетната отправна система? Както е показано на картинката по-горе, началото на ракетната отправна система се е преместило от А' до В'. Тоест, от А'(0, 0) до В'(0, 0.667). В случая имаме времеви интервал Δt = 0.667, но нямаме разстояние, защото пространствените координатои са се сменили и така излиза, че Δх = 0. Тогава въпросът става как изчисляваме преминатото разстояние? Ако следваме логиката, би трябвало да смятаме разстоянието между А' и В' между моментите t'(0) и t'(0,667), при което разстоянието излиза Δх = 335250 и тогава v' = 335250/0.667 = 502624. Другият вариант е да се сметне Δх = В'(0.667) - В'(-0.833) = -335250. Или Δх = А'(1,5) - А'(0) = -335250. Ако смятаме по втория начин излиза, че Δt = 1.5 и в двата случая. Тогава скоростта излиза v' = 335250/1.5 = -223500. Така че ако смятаме по този начи, сметките излизат (уж) както трябва. Само че като погледнем координатите се вижда какви трикове прави СТО. Първо В' е в миналото (отрицателен координат), независимо, че ракетата не е стигнала до В'. А след това А' отива в бъдещето (положителен координат), независимо, че ракетата вече е подминала А' и никога повече няма да се върне там.
-
Не съм пояснил защо имаме две времена. Според СТО за всяка точка се трансформират както пространствените, така и времевите координати. Ето пак координатите, този път с изпуснатите времена: Въпросът е как мерим скоростите и движението. В отправната система на земята, движението е от А(0,0) до В(223500,1). От тук изчисляваме разстоянието Δх = 223500 и времевия интервал Δt = 1. В отправната система на ракетата, движението е от А'(0, 0) до В'(0, 0.667). Пространствените координати и на двете излизат 0, защото ракетата си седи на едно място, а координатите на точките се сменят. Те са подвижни. За интервала Δt' = (0,667 - 0), координатът на А' е станал от 0 на -335250, така че Δх' = 335250 км. От там и скоростта излиза 335250/0,667 = 502624. Същото, ако погледнем В': за интервала Δt' = (0,667 - 0), координатът на В' се е сменил от 33520 на 0. Така че пак имаме Δх' = 335250 км и v' = 335250/0,667 = 502624.
-
Като цяло, Лоренцовата трансформация може да се опише като: ако х = сt , то х' = сt' ако х = vt , то х' = v't' Тоест, докато скоростта на светлината не се трансформира, то другите скорости неминуемо се трансформират. Няма как иначе. И както се вижда по-горе, като трансформираме v -> v', получената v' излиза по-висока от светлината.
-
Ами точно тази величина не ти трябва. Движението на ракета е от точка А(х=0, t=0) до точка В(х=223500, t=1). Така че v = Δх/Δt = 223500/1 = 223500 км/с. В ракетната система движението е от съответните точки А'(х'=0, t'=0) до В'(х'=0, t'=0,667). Само че в момент t'=0,667, координатите на А' вече са други, защото тя се движи. Така че v' = Δх'/Δt' = 335250/0,667 = 502624 км/с. Имай предвид, че Лоренцовата трансформация съществува, за да запази скоростта на светлината константна във всички отправни системи. Или казано по други начин: х = сt => х' = сt' Направи сметките и ще видиш как излизат.