Станислав Янков
Потребител-
Брой отговори
2763 -
Регистрация
-
Последен вход
-
Days Won
1
Content Type
Профили
Форуми
Библиотека
Articles
Блогове
ВСИЧКО ПУБЛИКУВАНО ОТ Станислав Янков
-
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
Може и така да се окаже, но е отличен стимул за мен да разбирам все по-сложни неща, до които само допреди половин година дори и не съм си мечтал, че ще започна да се докосвам (конкретно - линейната алгебра засега, но ще видим и за повече в бъдеще). И все пак, твърде е рано за траурни камбани - хиперизмерността и разнообразието от всевъзможни проекции предоставят твърде големи възможности, за да се заявява просто така, че целта ми е свръхнепосилна и нерешима. -
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
Това са съвсем официални Стрели на времето ( Arrow of time - Wikipedia ) и въобще не е изненадващо, че са толкова много, защото никъде не е заявено, че въпросът относно естеството на времето обезателно трябва да бъде лесен за разрешаване! Да не говорим, че има и философски разсъждения (разни!) относно времето (и пространството) - Philosophy of space and time - Wikipedia ... А би могло и ВСИЧКО около пространство и време и всякаквите процеси и континууми да се дефинира като вид ВЪТРЕШНИ особености, защото цялата човешка функционалност, особено в мисловната област и визуалните представи, е ИЗЦЯЛО продукт на мозъчни процеси - просто въображение, въображаеми картини, представи и зависимости/закономерности и нищо друго... И така да няма никаква пречка като "измерение", "пространство", "време" да могат да се определят ВСЯКАКВИ неща... Аз се отказах от опитите да намеря по-пълно и завършено определение и обяснение на времето (имах такива наивни надежди по едно време, преди да видя, че алтернативния изцяло пространствен хиперизмерен подход не решава въпроса с естеството на времето - то е нещо много по-сложно от просто едно пространствено измерение в повече от използваните сега три). В момента единствено търся най-точното съответствие между пространствено-времевите Специална, Обща теория на относителността и Квантова механика (квантовата теория на полето интегрира пространствено-времевата СТО, макар и това да не се случва лесно и безпроблемно) и между изцяло пространствена хиперизмерна концепция със същия брой пространствени измерения (четири), като пространство-времето на Минковски от теориите на относителността. И вече съм убеден, че не съществуват варианти без наличие на хиперизмерно (извън трите обичайни пространствени измерения) ускорение, тоест - вариантите с равномерно праволинейно движение на вселенската материя по координатата на четвъртото пространствено измерение w не вършат никаква работа (такова равномерно праволинейно движение не би могло да се регистрира по никакъв начин, както не може да се регистрира равномерно праволинейно движение на космически модул с космонавти в плоското 3D-пространство хyz на Космоса). Макар и движението по направлението на координатата w да е с постоянната скорост 1с, то може да е по спирала и поради това да е свързано с ускорение (кривината на спиралата, по която вселенската материя като цяло се върти с постоянната скорост 1с, когато става дума за покой в 3D-пространството хуz). -
Аз не бързам за никъде, важното е разбирането ми да се задълбочава, а не да се надпреварвам с хора, чиито познания превъзхождат моите много пъти. Затова и аз се ограничавам само до четири измерения, макар признаците да може да става дума за повече от четири измерения да са доста. Нека се изчерпят всички възможности с четири измерения и тогава може да се добавят още и да се види какво ще стане. Цитираното от теб изглежда като подобна алтернатива на суперструнната теория. Явно не е същото, но точно като при суперструнната теория допълнителните пространствени измерения над три се проявяват във връзка с взаимодействията. А пък торсионното (усукващо) движение много наподобява някои особености от туистърната теория на Пенроуз (тя е и десет-измерна, и осем-измерна и по-малко, та до обичайното пространство-време и трите обичайни пространствени измерения, в зависимост от това, какви аспекти на теорията се разглеждат и доколко включват те комплексния анализ). Прави впечатление, че има МНОГО-МНОГО голямо сходство между всички опити за нови теории и това е така, защото разработчиците им се стремят максимално, според възможностите си, да се съобразяват с потвърдените теории на относителността и квантовата механика. Така могат да се правят опити с всевъзможни, най-различни детайли, но общите концепции имат доста сродни очертания. Навсякъде можеш да откриеш близки съвпадения с елементи от други теории и предположения.
-
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
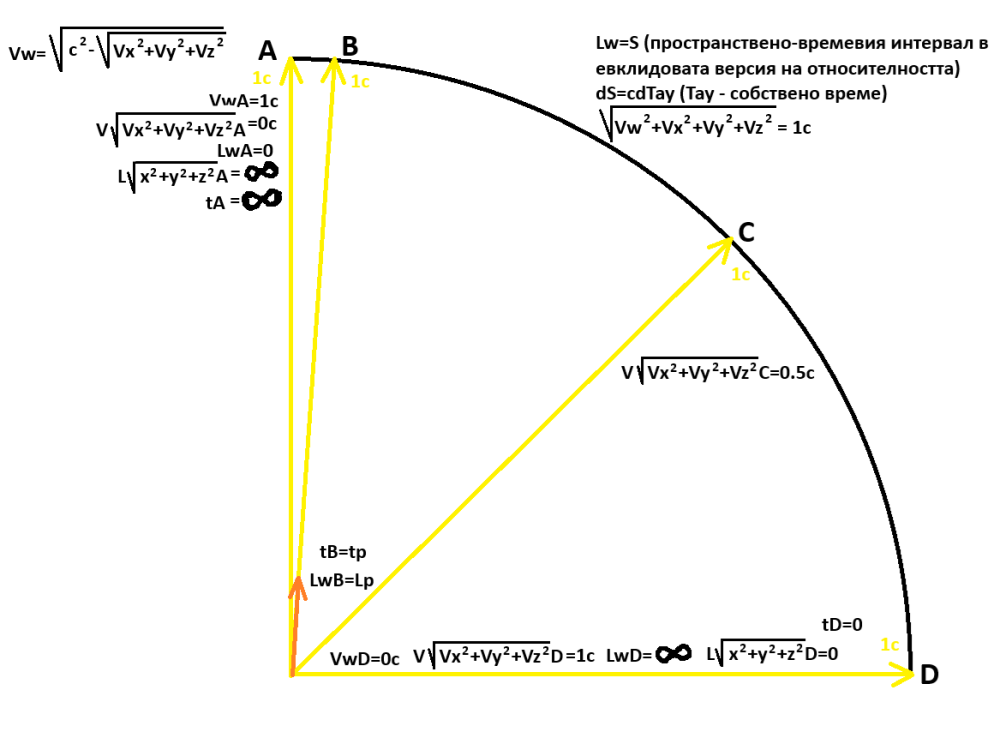
Естеството на времето, неговото пълно и взаимосвързано обяснение, представлява най-голямата загадка за момента. Тука се включват изключително много неща, има множество Стрели на времето, от най-различно естество - и термодинамична Стрела на времето (връзката с ентропията), и причинно-следствена Стрела на времето (свързана с теориите на относителността), и космологична Стрела на времето, и квантова Стрела на времето, а има още и психологична/перцептивна Стрела на времето, радиационна Стрела на времето, слаба асиметрия-Стрела на времето и може би още други... Дори при Евклидовата относителност векторът 1с може да бъде представен и не като скорост, а просто като безразмерно число, равно на единица и за следващи изводи да се ползват ъглите на завъртане между координатите на координатните системи (синус и косинус от този ъгъл и т.н.)... Въпросът с времето е все още толкова изключително сложен, че скоро едва ли ще се лишим от тръпката около решаването на купищата загадки във връзка с него! -
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
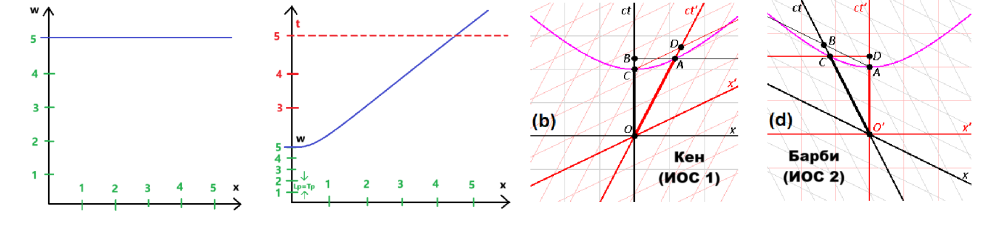
Не може без динамика, защото това е една от неизбежните разлики между пространтвено-времевите концепции и техни изцяло пространствени аналози - при пространствено-времевите концепции накрая се достига до статични форми и редуващи се техни срезове (четиримерни "самуни", които се нарязват на "филийки при Блоковата Вселена), докато чисто пространствените аналози са в перманентно движение с универсален темп 1с в хиперизмерното пространство. В пространствено-времевия случай покоят е базово състояние и движението е условност, докато в чисто пространствения аналог е точно обратното. При квантовата механика квантово-механичното обяснение би могло да се постигне алтернативно чрез особеността на диаграмите на Епщайн, че при пълен съвпад на вектора на четиримерната скорост 1с с вертикалната позиция А, времето става "безкрайност", което означава, че всичко в минало, настояще и бъдеще се случва едновременно (при движение със скорост на светлината изцяло в 3D-пространството хуz, позицията D, времевият темп е нулев, което значи, че часовниците са спрели). Доближаване към подобно състояние може да се свърже с едновременното движение на елементарни частици по всички възможни пътища при квантовата механика. Математически заплетените състояния са просто тензорни произведения на векторни състояния, които дават комбинирано геометрично пространство на двете системи - пространството на заплетената система (суперпозицията е линейна комбинация на вектори на състоянието, мащабирани чрез константи за мащабиране и така се получава по-сложен вектор на състоянието в резултат). -
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
Тази в материала от линка не се движи по никакъв начин, дори не се върти по някакъв по-прост или по-сложен начин. Тя е статична. Особено в ОТО се ползват особеностите на сферичността и специално тази на хиперсферите, "наблюдавани" (техните особености като пространства) "отвътре", но и там не става дума просто за статична хиперсфера. В ОТО хиперсферичните идеи и въобще хиперизмерността са прилагани по много сложни, абстрактни и неинтуитивни начини. Иначе няма спор, че ако е възможно пълноценно и цялостно обединяване на квантовата механика и общата теория на относителността - най-вероятно няма да може да се мине без хиперсфери, хиперкубове и други хиперизмерни форми. Само употребата и за двете на един и същи математически (геометричен?) "език" (подход) има шанс да се забележи онази плодотворна пътека, която да позволи пълното и последователно обединение и на двете. Аз лично съм твърде далеч от подобна амбиция и засега се ограничавам само до намирането на вярно еквивалентно описание на пространствено-времевите СТО и ОТО единствено чрез пространствени измерения и различни проекции (начина да се дефинират процеси с различни пространствени размерности - процеси с едно, две, три, четири и повече измерения), без никакви условни измерения и така употребата на различните хиперизмерни форми В ДВИЖЕНИЕ (хиперсфери, хипер-кълба, хипер-кубове и всякакви други) е неизбежна, само е много важно удачно да се избира кога-какво и с каква измерност да се прилага. -
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
В линка е дадена просто хиперсфера, което може да бъде и три-сфера (обичайната сфера, "покривката" на кълбо, е дву-измерна), и с още повече от три измерения. Още в ОТО се разглеждат доста сложни моменти, които не се ограничават само до сфера (например плоското, евклидово пространство-време при СТО, когато няма гравитационно въздействие и така няма нищо общо със сфера, даже и условно). Хиперизмерността в теориите на относителността, даже и условна, под формата на четири-мерно пространство-време, се проявява по доста сложен и неинтуитивен начин, понеже се "разглежда" "отвътре", без помощта на условно евклидово пространство с допълнително измерение, чрез което да се анализира кривината на геометрията "отвън" ("вътрешното" разглеждане, като "вътрешни" свойства и особености на геометрията, се разглежда детайлно от римановите геометрии). Евклидовата относителност извън това, над което се мъча аз, се оказва, че не включва ясно дефинирано четвърто пространствено измерение w (само има някакви бегли намеци за такова четвърто пространствено измерение в малка част от всички материали, свързани с Евклидовата относителност), нито е чак толкова проста и интуитивна, колкото твърдят застъпниците ѝ. В общи линии Евклидовата относителност е пространствено-времева концепция, точно както и концепцията на Минковски, само някои членове в метриката ѝ са разместени така, че хиперболичното завъртане между координатите в диаграмите на Минковски да може да се пресъздаде точно чрез завъртане между координатите по обичаен, евклидов кръг (от там и минусите във формулата за намирането на пространствено-времевия интервал от Минковски стават на плюсове при аналогичната формула от Евклидовата относителност и при втората служат за намирането на сt2, вместо на пространствено-времевия интервал s). Евклидовата относителност досега е нещо започнато и недовършено, недоработено до пълноценна алтернативна концепция на неевклидовото (псевдо-евклидово при СТО и псевдо-риманово при ОТО) пространство-време на Минковски. Пълноценната алтернатива на пространство-времето на Минковски е съответстваща, напълно еквивалентна (което не определя пространствено-времевата концепция на Минковски като невярна), изцяло пространствена концепция със същия брой измерения, която надхвърля представените досега версии на Евклидовата относителност. При пълноценна чисто пространствена алтернатива на Минковски условното времево измерение се замества от условно екстраполиране на крайния w-базов вектор от състояние в покой върху реално безкрайните базови вектори на останалите координати х, у и z. И понеже става дума за базови вектори, които принципно биха могли да бъдат съвсем произволни - след обособяването на асиметрията между четирите неслучайни в случая с алтернативната концепция базови вектора w, x, y и z и преодоляването на тази асиметрия чрез условната екстраполация, няма пречка физическата реалност да се опише и чрез пространствено-времевия подход на Минковски, и чрез алтернативен изцяло пространствен подход (двата различни подхода представляват съответствие помежду си). Затова и за момента алтернативната концепция все още не дава нищо повече, което да не би могло да се получи и чрез утвърдената пространствено-времева концепция на Минковски (тоест - до момента се занимавам с нещо интересно за мен, но все още безполезно). -
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
Дали пространството е безкрайно или крайно, но клонящо към безкрайност - и при двата споменати от теб подхода ще може да се приеме, че условно пространството е безкрайно (евклидово). Точно като хиперизмерната и триизмерната светлина - и двете имат вълново естество (спомни си вълните на неопределеността в квантовата механика и вълновата компонента на елементарните частици, които там не са точно вълни или по-точно са вълни на състоянията, но всичко това вероятно може да се представи и като реални вълни в четириизмерно пространство, пак като съответствие с настоящия верен квантово-механичен подход). Точно както може да се изгради пълно съответствие между пълноценно четириизмерно пространство и четириизмерно пространство-време (при диаграмата на четириизмерното пространство координатата нагоре е не само времева, собственото време сТау, където времето е само параметър, а не измерение, но и координата на четвъртото пространствено измерение w, което представлява базовия вектор на тази координата). -
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
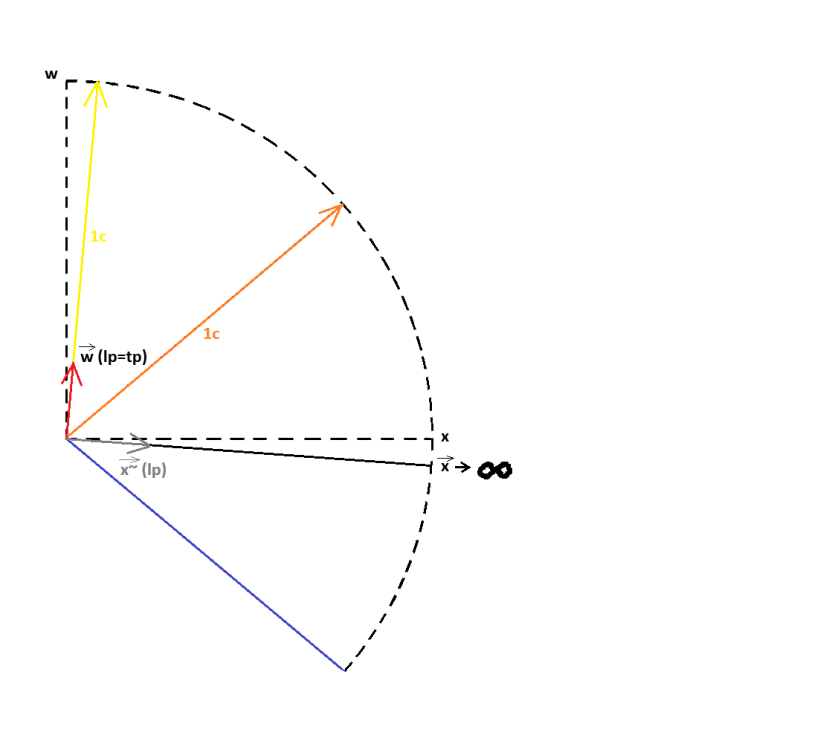
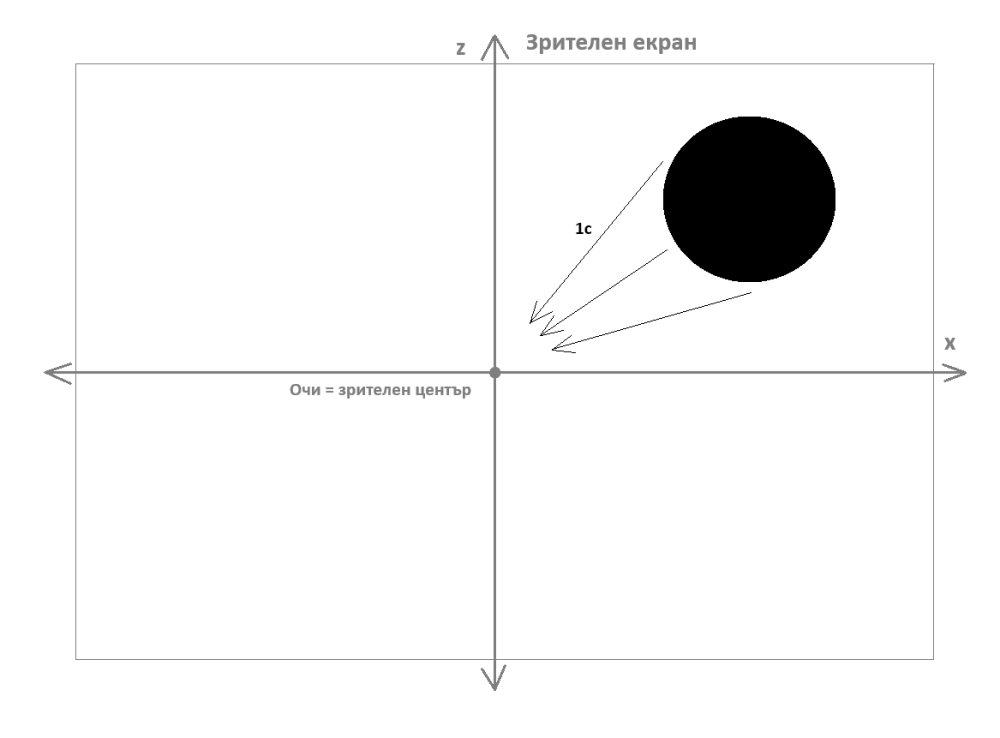
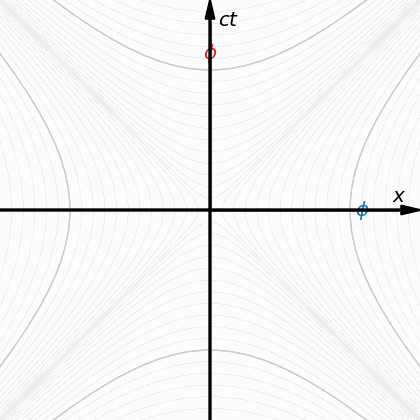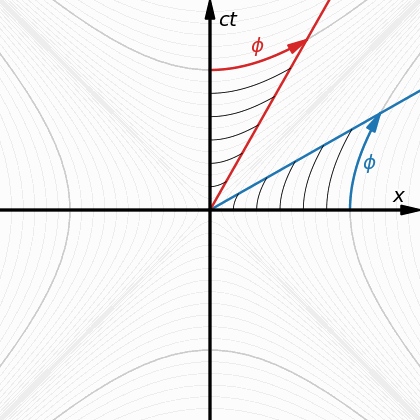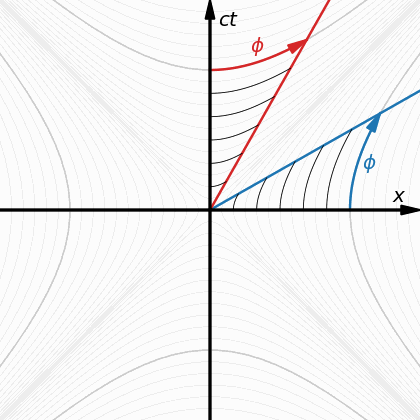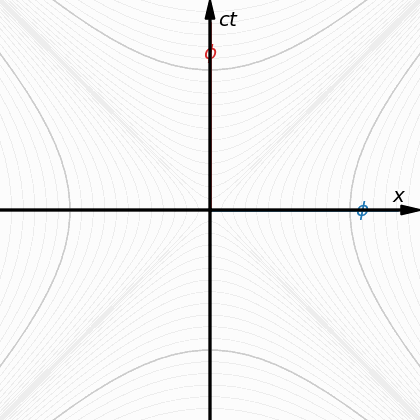
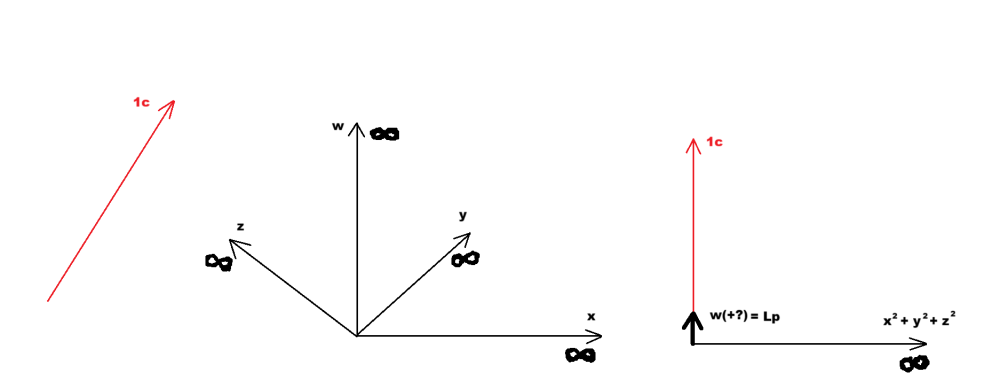
Взаимодействията и по-специално електромагнитното и гравитационното (макроскопичните взаимодействия, най-вече електромагнитното - зрението и осезанието, допира, са електромагнитни феномени) са средствата за регистриране и дефиниране на произволни обекти в пространството. Например, отчитането на неподвижно черно кълбо в пространството става чрез отразените или излъчените от него лъчи, които попадат в зрението или в светлинни сензори (фотоапарати, камери и прочее). За да могат да се оценят подобни ограничени в пространството обекти, планковата дължина по направлението на координатата w в асиметричното 4D-пространствено многообразие wXУZ от състоянието в покой се екстраполира и върху обединената три-пространствена координата корен квадратен от х2+у2+z2. Реално, дали протяжността в покой на трите координати х, у и z е безкрайна или някаква друга се определя от космологичната геометрия на вселенското пространство (елиптична, хиперболична или евклидова). Всеки регистриран обект представлява на практика друго (различно) 4D-пространство, което счита себе си за покоящо, точно както се счита за покоящ и наблюдателя и кога и как тези различни пространства встъпват във взаимодействия помежду си (електромагнитните и гравитационните взаимодействия на макро-ниво), се определя от особеностите на 3D-светлината и на 4D-светлината (хиперизмерната светлина, векторът 1с по направлението на координатата w в първото изображение) във връзка с тях. Изглежда тук моите предположения и опити за съставяне на изцяло пространствен 4D-подход (който много лесно може да се окаже и над-4D!) започват все повече да се отличават от другите подходи около Евклидовата относителност, макар Хосе Алмейда с неговата "4D-оптика" да се доближава в някаква степен до всичко това - трябва да проверя по-внимателно тази работа! -
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
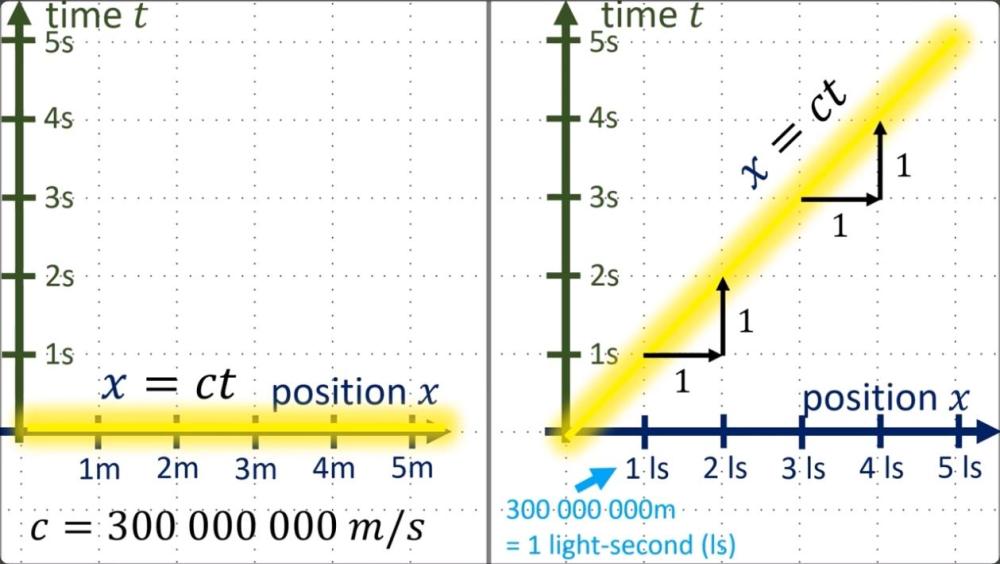
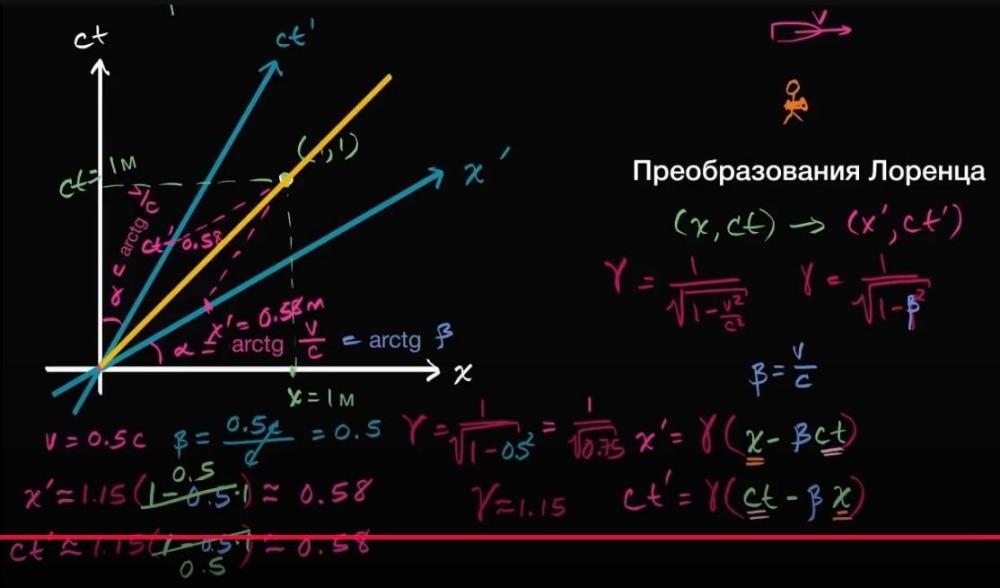
Ето пример за съответствие пряко от Специалната теория на относителността, който ясно показва, че могат да се ползват всякакви базови вектори, когато споменатото съответствие е налично: Обичайно параметрите на базовите вектори са секунда по координатата t и метър по координатите х, у и z и няма фатални проблеми СТО да си работи и по този начин (само е по-неудобно). Вместо това, най-често във връзка със СТО се ползват различни от споменатите базови вектори, а именно - сt или светлинни секунди за координатата t и приблизително 300 000 километра за координатите х, у и z. Това е пряк пример от Специалната теория на относителността за безпроблемната употреба на различни базови вектори, когато двата различни случая са свързани с пълно съответствие помежду си. -
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
Метриката в 3D+1D пространство-времето на Общата теория на относителността е псевдо-риманова (тази на 3D+1D пространство-времето на Специалната теория на относителността е псевдо-евклидова) - използват се квадратични уравнения, които могат да имат и компоненти с отрицателен знак, за разлика от стандартната Питагорова теорема, където знаците пред всички компоненти на уравненията са само положителни. Аз имам предвид съответствие между пространствено-времевата концепция на Минковски и алтернативна изцяло пространствена концепция със същия брой измерения. Не аналогия (подобие), при която да съвпадат само ограничени елементи между двете концепции, а пълно съответствие, при което всяко нещо от едната съвпада с нещо от другата, даже и някои детайли да не са напълно еднакви в някои отношения (пространствено-времевия подход представлява статична Блокова Вселена на съвместно минало, настояще и бъдеще, при която отделните моменти от настоящето представляват последователни срезове от общия минало-настоящо-бъдещ "блок" на Блоковата Вселена, докато алтернативния, изцяло пространствен подход се базира на перманентно движение на вселенската материя с константен темп 1с в хиперизмерното пространство, докато движенията в 3D-пространството представляват проекции с различни скорости в 3D-пространството между 0с и 1с). И също така - не пространствено-времевата концепция на Минковски или алтернативната изцяло пространствена да са неверни. И двете различни концепции са верни и тясно свързани със съответствие помежду си, точно като двете различни страни (предна и задна) на една и съща монета (реалността) или като съответствието между външната и вътрешната диференциална геометрия. Разликата между 3D+1D пространствено-времевата концепция и 4D изцяло пространствената концепция се корени само в една област (но със сериозни последици на следващите равнища, на които тази област се явява фундамент) - координатните системи на пространствено-времевата концепция разчитат на равностойни базови вектори при формирането на мрежите и координатите на системите, докато базовите вектори на изцяло пространствения 4D-подход са асиметрични: Както знаем от линейната алгебра, базовите вектори в основата на различните координатни системи могат да са най-различни, стига тензорите (инвариантните параметри) да остават едни и същи според всички различни координатни системи. Защото това е основната функция на макроскопичната физика - да показва, как се описват разни събития, обекти и движения на обекти в различните координатни системи, как протичат различни трансформации: Дали се ползват напълно симетрични или асиметрични един спрямо друг базови вектори - няма драматично значение, когато между двете концепции, макар и различни една спрямо друга (едната пространствено-времева, а другата изцяло пространствена) има пълно съответствие (няма особености на единия подход, които да не могат да бъдат представени чрез особености на другия подход, макар да става дума за страшно много работа, защото досега всичко във връзка с потенциалния изцяло пространствен подход е само в съвсем начален зачатък). Нерешените въпроси са много, но и потенциалът е добър - все пак говорим за хиперизмерно пространство и всякакви проективни техники (елиптична, хиперболична, гномонична, стереографска...)! Единствено аз не съм подходящия за тази работа (физичните ми познания са видимо доста повърхностни), но - с това разполагаме за момента... -
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
Аз имах предвид друго - примера с птицата като метафора на моите усилия. От една страна може просто да се отговори, че пространство-времето не може по никакъв начин да се представи чрез изцяло пространствени измерения и без времето (или каквото и да било друго, различно от пространствено) да е измерение - пространство-времето е развито до невероятни степени, а за другото няма нищо сериозно ("Много хубава задача — поетична, но и математически наситена. Нека съчетаем образа на гигантския буревестник и динамиката на тайфуна в една символична формула."). От друга страна - пространствената хиперизмерност и проективните техники дават изключително богати възможности, макар да няма начин за алтернативно пресъздаване на пространствено-времевия подход, който начин да не е изключително сложен дори за много по-добре подготвени от мен във физичната (и математическата) област. И през ум не ми е минавало да отричам, че има страшно-сложни (и точни) физически начини за представяне на полета на птицата! -
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
Аз не съм чел техни работи. В друга тема ("Въвеждане на допълнителни измерения във физиката и ползите от тях") преди време Кипен ме разкритикува, че съжденията ми били подобни на езотеричните твърдения на Успенски за четвърто измерение и затова не трябвало да пиша в раздел "Физика". Тогава ми стана интересно какво има предвид и си изтеглих някаква книга на Успенски, в която се говори и за това четвърто измерение (покрай купища други неща), но все още не съм успял да прочета за какво точно става въпрос - не разбирам стотици неща от физиката, които считам за важни в момента и още по-лошото е, че всичко това прилича на лавина: за колкото повече неща успявам да науча и поразбера нещо - толкова още повече неща изникват като важни, за които не знам нищо! При най-повърхностния ми поглед засега, попаднах някъде на кратък синтез за Успенски и Гурджиев, който ми допадна като за начало: "През 1907 г. започва увлечението на Успенский по езотеричните учения като в началото го интересували "висшите измерения", за които науката не знаела нищо. Пътешествувайки на Изток, Успенский се запознава със системата на Йога, европейския окултизъм, пише книги (най-значителната, от които е "Tertium Organum"), чете лекции в Москва и Петербург. Завръщайки се в Русия след поредното си пътешествие, непосредствено след започването на световната война, Успенский се среща с Г. И. Гурджиев, през пролетта на 1915 година. Тази среща слага отпечатъка си върху целия по-нататъшен живот на Успенский. В Гурджиев той намира всичко онова, което дълго и безуспешно е търсил на Изток: логическата система, школата по медитация, разработената техника за достигане на "висшите измерения". Сътрудничеството на Успенский с Гурджиев, обаче не било дълготрайно. Попречили не само революцията и гражданската война в Русия, но и несходството в характерите и стремежите на учителя и ученика. Окончателният разрив между двамата станал през 1924 г., когато са били вече в емиграция, макар че Успенский продължава да счита себе си за последовател на Гурджиев. Своите дореволюционни публикации, Успенский преработва в духа на усвоената от него система. През 1931 г. излиза на английски неговият "Нов модел на Вселената". В последствие Успенский работи над създаването на психологическа теория, откъси от която се съдържат в лекциите "Психология на човешките еволюционни възможности". Успенский умира в Лондон през 1947 г. След смъртта му, ръкописът на книгата "Фрагменти от едно неизвестно учение" бил изпратен на Гурджиев и публикуван от него на английски език със заглавие "В търсене на чудотворното". Гурджиев не притежавал таланта на популяризатор и пропагандатор. Тези функции поел Успенский, който със своите книги и лекции разпространявал учението му. Лекциите, четени в Лондон и Ню Йорк, били предназначени за запознаване със системата на Гурджиев в такава форма, каквато й придава Успенский. В началото той прочел пет лекции по космология, съдържанието на които, в основата си, съвпадало с по-късно публикуваните "Фрагменти от едно неизвестно учение". Следвали пет лекции по психология. Обикновено някой от старите ученици четял лекциите пред групата на "неофитите"(новоприетите ученици). Понякога Успенский присъствал на четенето на лекциите, а след това отговарял на поставени въпроси и изнасял беседи. Своеобразието на текстовете се обяснява с това, че целта им била не само запознаването на слушателите с нови знания. Те били предназначени за тези, които са започнали да се "пробуждат", които са поставили под съмнение науката, започнали са да търсят нещо по-различно. На тези хора им била необходима школа и много от слушателите на лекциите на Успенский се отправили към Фонтенбло, където през 20-те - 30-те години действувала школата на Гурджиев. Много видни интелектуалци са слушали тези лекции, достатъчно е да споменем О. Хаксли. Първоначално, "Психологически лекции 1934г. - 1940 г." били публикувани на английски език в незначителен тираж през 1940 г. и съдържали шест лекции. В последствие заглавието било променено на "Психология на човешките еволюционни възможности", а количеството на лекциите, съкратено на пет. В някои издания, освен лекциите "Бележки за решението да се работи", е включена и автобиографията на Успенский. Учението на Гурджиев, главен теоретик и пропагандатор на което бил Успенский, получило широка популярност на Запад. Към загадъчната фигура на Гурджиев не веднъж са се обръщали интерпретатори: достатъчно е да споменем книгата на Л. Поуел, филма на Питър Брук: "Срещи със забележителни хора", разказващ за духовните търсения на Гурджиев през младежките му години. Школата на Гурджиев включвала обучение по музика, танци, специалния балет на Гурджиев", техниката на медитацията. Някои изследователи посочват синтетичния характер на доктрината: освен елементи на йога, в нея влизат и елементи от други източни езотерични учения, преди всичко на "суфитите". Биографията на Гурджиев е непозната в подробности и ние едва ли ще изясним днес, откъде и кога той е получил своите познания. Във всеки случай Учението, което преподавал, се е отличавало от всички теософски учения по това време, със своята непосредствена връзка с първоизточниците. Пишейки за Четвъртото измерение, по материали на съвременната физика и математика, добре запознат с естествознанието на XIX век, Успенский внася в изложението на тази, източна по своя произход доктрина, редица новости. От тук идва и своеобразното съчетание на механистичната физиология и психология със Законите на Карма, съчетаването на тайните учения с математиката и даже с ницшеанската доктрина за свръхчовека (осмислена в религиозно — философски дух) в "Новия модел на Вселената". Такова съединение на рационално — научната аргументация и техниката на медитация, в известна степен е характерно и за лекциите "Психология на човешките еволюционни възможности". За осъзнаването на необходимостта и възможността за "вътрешно развитие", е необходимо да се разбере механичността на съществуването, безсмислието на прекарания в "буден сън" живот. Разбира се, става дума не за религията на спасението, а за източната доктрина за "освобождаването", като се подчертава далечния характер на източните учения от гледна точка на западноевропейския начин на живот. Това Учение е интересно и от историческа гледна точка. Интересът към Изтока и преди всичко към Индия, е бил характерен за руската интелигенция от началото на века и "Феноменът Гурджиев-Успенский" е не по-малко значим в този смисъл, от например, "Феноменът Рьорих". Ето защо е необходимо да се преиздадат дореволюционните работи на Успенский, преди всичко "Tertium Organum", но не по-малко значими са и публикуваните в емиграция произведения - "Новият модел на Вселената" и "Фрагменти от едно неизвестно учение". Публикуваните лекции не дават пълна представа за дадената "школа". Те представляват интерес в друго отношение: бидейки своеобразен синтез на съвременната наука и източната философия, лекциите представляват пример за съединяването на две разнородни по своята същност форми на познанието. Те бяха избрани защото от тях достатъчно ясно, се виждат особеностите на съвременния окултизъм в една от най-добре разработените му логически форми." Накратко, Успенски определя броя на измеренията като 7 - три пространствени три времеви и седмото е квинтесенция на шестте на по-висше ниво. Не зная дали това е свързано с Успенски, но: "От великото Нищо, което няма форма или продължителност - произлязла една единствена точка.Това е азът, който носи безкраен потенциал, който още не се е проявил и превърнал в качество. Това в съществуване в нищото на пространството, представено от една единствена точка или място. Жизнеността на единствения аз поражда резониращ пулс, който разстяга точката, докато се отрази в своята собствена субстанция, за да стане аз съм. Tака създава измерение в пространството. Това измерение има дължина, но няма ширина или височина. То се означава с линия, и е Първото Измерение. Когато това, което отразява или се отразява се разглежда в по-висша перспектива, тогава се създава повърхност - Второто Измерение, което има дължина и ширина, но няма дълбочина. Още в древността било изобразявано като триъгълник. Чрез "преместване" на осъзнание над дължината и ширината, се ражда Трето Измерение - това е на дълбочината , която осигурява стабилност на формата. То се изобразява като триъгълник върху квадратна основа и изразява концепцията за форма, която се ражда от една единствена точка, точка в нищото на пространството. Представата за дистанция създава Четвъртото Измерение - измерението на трайността, което наричаме време. Времето дава продължителност, в която формата може да се прояви и развие. физическият свят съществува в Четвъртото Измерение, макар, че създава усещане, че е вън от времето. Символ на Четвъртото Измерение е пирамида. Петото Измерение е съзнанието, което е отвъд и извън материята и няма продължителност, но и действа и се променя чрез измерението на времето. Именно посредством съзнанието човек осъществява своя избор. Шестото Измерение е душата. То е измерение на творчеството. Не съзнанието е извор на творчеството, а душата. Съзнанието е процес, през който творчеството може да се насочва, моделира и оформя. Седмото Измерение е духът, който е субстрат без форма, но намира израз и облагородява опита чрез формата. Той е първичният разум, който създава формата. Осмото Измерение е Ни-Щото, от което произлиза първичния дух. В Китай го назовават Дао. Индийците - "Великата Тайна". Има и следващо измерение, в което се събират всички измерения. Деветото Измерение е Земята: централната точка, средата на осемте измерения. Тя е мястото, в което всички измерения се проявяват едновременно. Това измерение се изобразява в древната символика като два взаимозависими триъгълника - единият насочен нагоре, а другия надуло, всеки с точна над своя връх и с око в средата." А пък на Кабала се приписва да намеква за 11 измерения (някакво Господарско число) - много забавно съвпадение с 11-те (когато не са 12) измерения на суперструнната теория! С това се изчерпва всичко, което съм успял да прегледам относно Успенски досега. Не-не! Целият ми фокус в момента е над въпроса, дали четиримерното пространство-време може по някакъв начин да се представи като четиримерно пространство (времето да не е измерение, а параметър, произтичащ от геометрията на вселената и от начина, по който я възприемаме и проектираме чрез сетивата и мозъка си). Мотивираха ме категоричните заявления тук, че не може, а аз въобще не съм сигурен, че е чак толкова невъзможно (хиперизмерното пространство и проекциите предоставят изключително големи възможности, за да се каже просто така, че не може и че пространствено-времевия подход е единствения релевантен и приложим). -
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
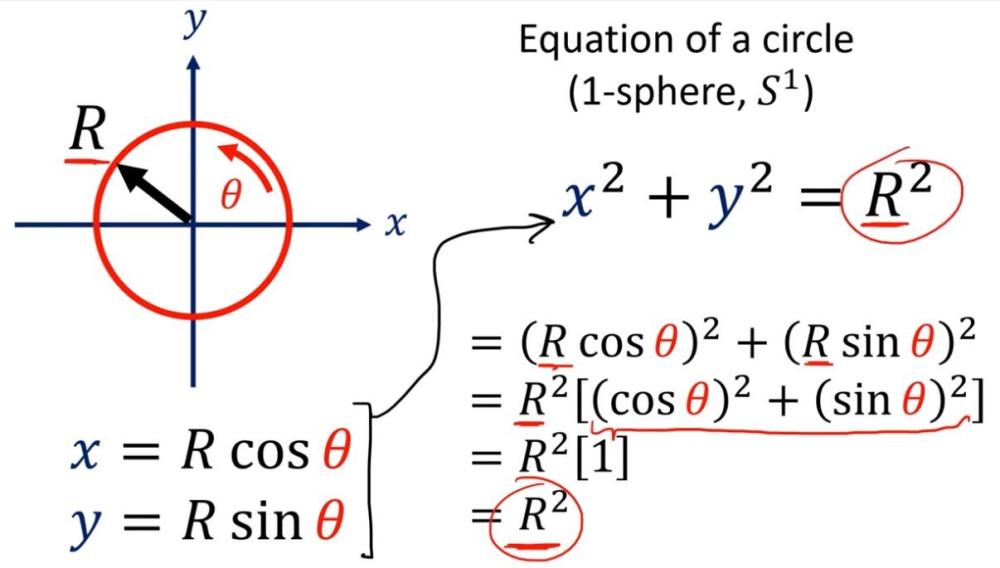
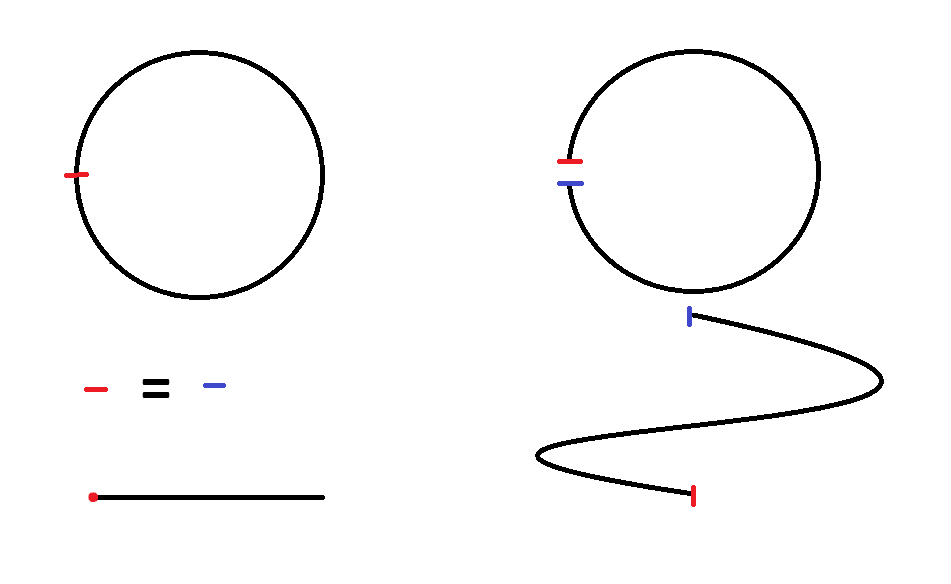
Принципно това не е необходима - всички необходими формули са налични отдавна и дори не са чак толкова сложни. Ето, например, как се описва окръжност (едномерна, в двуизмерно пространство): Също така, ако една окръжност се промени на спирала - при завъртането ѝ към поглед "отгоре" тази окръжност няма да може да се затваря, за разлика от когато не е спирала, понеже тогава има и пространство в трето измерение ("нагоре"): Всичко това, обаче, са твърде базови и начални разсъждения. Изключително голямото предизвикателство е да се изгради от всичко това някаква свързана и цялостна концепция, която да изразява всичко, което дават утвърдените сега теории, без досега да е работено в подобно направление почти по никакъв начин (може би има само някакви най-общи, без никакви детайли, споменавания в разни езотерични текстове - някакви споменавания от Успенски/Гурджиев, ако си спомням точно едни критики към мен тук, че съм се бил занимавал с нещо такова). И при това - занимавам се с това нещо точно аз, чиито физични познания и подготовка са, меко казано, скромни. Това значи, че ако е възможно изграждането на съответствие между четиримерно пространство-време и четиримерно пространство (а няма причина да не е възможно, защото това са просто два различни подхода за оценяване на едно и също нещо, четиримерната реалност, точно както външната и вътрешната гледна точка са два различни подхода за оценяване на едно и също нещо, кривината) - това няма да се случи лесно и скоро... -
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
Съответствията са ясно изразени в квантовата механика, макар да ги има и навсякъде другаде във физиката като цяло (например външната гледна точка, с допълнително измерение и обгръщащо пространство и вътрешната гледна точка на Римановата геометрия са съответствие - два различни, равноправни подхода на описание на едно и също нещо - кривините). Каноничното квантуване на Дирак е съответствие, както и принципът на съответствие на Бор преди това, който се е оказали неуспешен. Принцип на съответствие – Уикипедия -
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
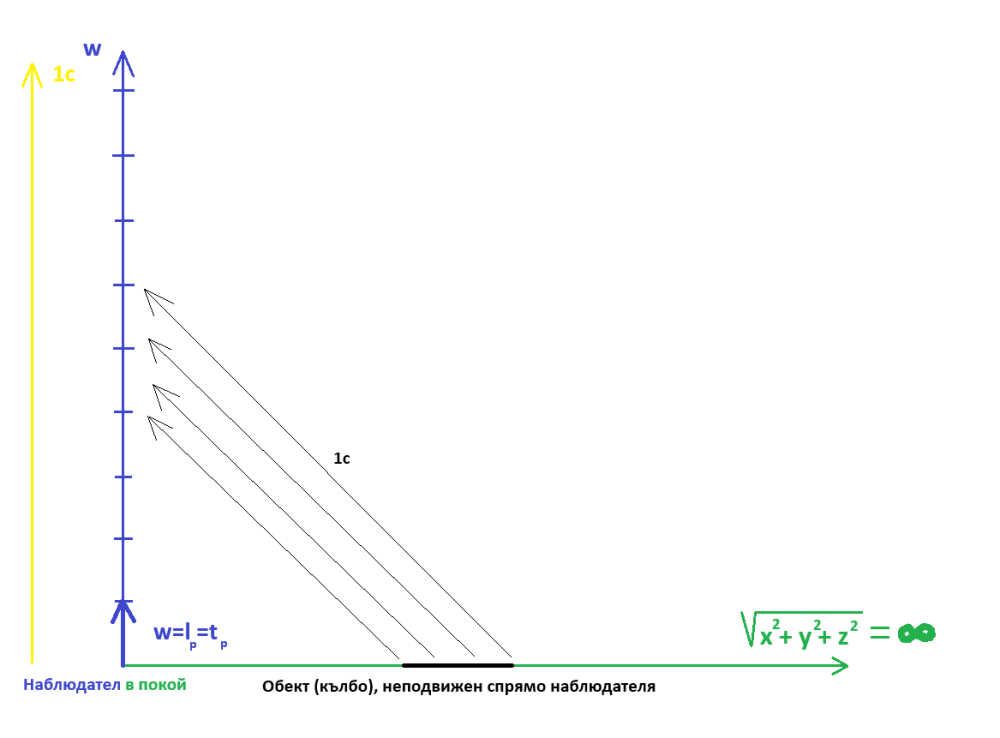
Когато нещо (произволен обект) се движи инерционно (по права линия и с една и съща скорост), то не усеща движението и счита себе си в покой. Това означава, че ако има четвърто пространствено измерение w, то не само базисния вектор по направлението на координатата w, при покой в 3D-пространството хуz, е съкратен до планковата дължина (равнозначна на планковото време), поради движението на цялата триизмерна координатна система с темп 1с по направлението на координатата w, както е показано на долното изображение но има и огъване на същото това движение в спиралообразна форма, което значи наличие на ускорение (ситуацията b на следващата фигура): Ако движението на цялата 3D-координатна система хуz по направлението на w беше просто с темп 1с по права линия, това щеше да бъде обикновено инерционно движение и нямаше да може да се регистрира никакъв времеви ефект. Понеже обаче това движение е с ускорение, заради спиралоподобното му естество по направлението на измерението w, то се регистрира като часовников темп при покой в 3D-пространството хуz. Дали спираловидната кривина се простира в триизмерното пространство хуz или е изразена в пето пространствено измерение (даже и едномерна, една окръжност не може да бъде представена по начин, различен от правата линия на нейния диаметър, ако това представяне не се случва в двуизмерно пространство - външната гледна точка през евклидово пространство с едно допълнително измерение) - това е отворен за размисъл въпрос (гравитацията получава някакви сякаш перспективни обяснения при пет измерения, макар и да става дума за пространство-време). Това е едва първи опит за анализ в подобно направление и е силно спекулативен и недоработен. Просто начало, за да може да се почне от някъде с проверките за точно съответствие между симетрично четиримерно пространство-време (обичайното евклидово проктранство-време от СТО и ОТО) и несиметрично четиримерно (или дори над-четиримерно) пространство, където базовите вектори по направленията на координатите хуz и по направлението на координатата w(+?) не съвпадат (не са симетрични, не са еднакви, макар и да са ортогонални един на друг). -
Какво е точното пресъздаване на особеностите на пространствено-времевите теории Специална и Обща теория на относителността посредством хиперизмерен (над-триизмерен) пространствен подход? Има ли място подобен подход по отношение на квантовата механика?
Станислав Янков отговори на Станислав Янков's в Теоретична Физика
Много странно! Не намирам нищо за физическо обяснение на съответствие (correspondence), а това е особеност, която присъства не само в AdS/CFT-съответствието и в dS/CFT-съответствието! В диференциалната геометрия има разграничението на външна и вътрешна гледна точка: "От началото и до средата на 19-ти век диференциалната геометрия е изучавана от външна гледна точка: кривите и повърхностите са разглеждани като лежащи в евклидово пространство с по-висока размерност (например повърхност в обгръщащо пространство от три измерения). Най-простите резултати са тези в диференциалната геометрия на кривите и диференциалната геометрия на повърхностите. Започвайки с работата на Риман , е развита вътрешната гледна точка, при която не може да се говори за движение „извън“ геометричния обект, защото той се счита за даден по самостоятелен начин. Основният резултат тук е теоремата на Гаус за егрегиума , според която Гаусовата кривина е вътрешен инвариант. Вътрешната гледна точка е по-гъвкава. Например, тя е полезна в относителността, където пространство-времето не може естествено да се приема като външно. Има обаче цена, която трябва да се плати, под формата на техническа сложност: присъщите дефиниции на кривината и връзките стават много по-малко визуално интуитивни. Тези две гледни точки могат да бъдат съгласувани, т.е. външната геометрия може да се разглежда като структура, допълнителна към вътрешната. (Вижте теоремата за вграждане на Наш .) Във формализма на геометричното смятане както външната, така и вътрешната геометрия на многообразието могат да бъдат характеризирани с една единствена бивекторно- значна еднозначна форма, наречена оператор на формата ." Разграничението външна/вътрешна гледна точка е съответствие, точно както AdS/CFT-съответствието и dS/CFT-съответствието, само тук сравнението не е особености в даден брой измерения спрямо по-малко измерения, а даден брой измерения спрямо повече измерения (външната гледна точка, защото вътрешната гледна точка е друг вид съответствие - един и същи брой измерения, но през "евклидов екран" /допирателни и срезове/). Съответствията са приложими на страшно много места във физиката, а никъде не намирам никакво по-детайлно физическо обяснение за тях!!! -
То, като че ли самото дефиниране на някакъв обект по принцип става чрез светлината (която се улавя от очите ни и се обработва до визуално изображение от мозъка ни), че и тактилната чувственост (допир, топлина, студ) също е електромагнетизъм! Човекът възприема околния свят най-вече чрез светлината/електромагнетизма!
-
След Минковски и Айнщайн във физиката се използва съчетанието пространство-време (извеждането на времето от параметър към статута на измерение, което позволява употребата на диференциалната геометрия - преди това теорията на Айнщайн е била просто електродинамична теория с базиране върху Лоренцовите трансформации и с допускане за наличието на етер) и не става дума просто за пространство, а за многообразие (множество пространства, които се представят чрез вид картографиране). Принципно има едно пространство, в което е и се случва всичко, но също така могат да се разглеждат и множество негови подпространство, под формата на многообразие. Нещата са достатъчно сложни (потвърдено и доказано), за да не могат да се обяснят чрез по-елементарни и интуитивни концепции като Галилеевите трансформации Нютоновите пространство и време (абсолютни). След Айнщайн тези стари концепции (галилеевата и нютоновата за трансформации, пространство и време) са си изпели песента потвърдено, а новите неща са неприятно-сложни и неинтуитивни (затова и някои толкова много ги мразят и отричат!).
-
Чрез отстоянието между два материални обекта (две точки). Не съм го разбрал достатъчно добре, но предполагам не е грешно да се каже, че празно пространство (когато игнорираме квантовата механика) може да има, само когато има и гравитационни концентрации на материя/енергия. Ако не съществуват гравитационни концентрации до масивни обекти, не може да се дефинира и отстояние или празно пространство в макроскопичен смисъл между тях (няма да има точки, между които да се регистрира отстояние). Това не значи, че не могат да се изследват области на празно пространство или пък геометрията на пространството на Вселената (евклидова, елиптична, хиперболична), а че не може да се дефинира съществуване на отстояние/пространство без наличие на точки/материални обекти, между които да се простира това отстояние/пространство.
-
Защо си ги цитирал тези неща?! Първото е теоретичен (математически) часовник, предназначен да се използва с формулите и няма реално съществуване (както и светлинтия часовник, междувпрочем). А и за второто може да има нещо подобно:
-
Не да не съществува пространството (след като го регистрираме - значи съществува!), а няма смисъл без материални обекти (материя), между които да се дефинира. По-скоро може да се каже, че не съществува ПРАЗНО пространство само по себе си (освен като идеализирано понятие от философията, евентуално?), защото според квантовата механика в действителност празно пространство няма (навсякъде, дори в най-съвършения и дълбок вакуум, протичат квантово-механични флуктуации, а празно пространство, което да не е вакуум, не е известно да съществува реално, извън някакви евентуални съвършени идеализации).
-
Времето е ТОВА, което измерва часовникът, не самият часовник. Процесите са устройството на часовника (до мисловния светлинен часовник, който борави с движението на светлината, със скоростта на светлината, през пространството, а после и до идеалния часовник със съвършена точност и без никакво устройство и процеси, на които да се базира).
-
Може би по-плодотворно би било да започнеш с това - кой процес в квантовата механика налага скорост, по-голяма от тази на светлината? Умножаването на планковата дължина с планковото време дава стойността на скоростта на светлината във вакуум и затова тези две планкови единици въобще не са случайни (освен че произтичат от куп универсални константи). Квантовите заплитания нямат нищо общо със скоростта на светлината, защото не са свързани с обмен през пространството, който да налага надсветлинни скорости. Определено не съм най-сведущия по темата, но аз не знам нищо в квантовата механика (и извън нея), което да не може да се обясни и без закона за пределността на скоростта на светлината да се нарушава.
-
Когато времето е свързано с координатите на пространството като координата на измерение (времевото) - ефектът може да се визуализира геометрично (това са диаграми, но те боравят с линии, точки, дължини, ъгли и прочее геометрични средства, затова се нарича пространствено-времева геометрия) и така геометрията представлява обяснението и причината.