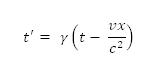gmladenov
Потребител-
Брой отговори
10473 -
Регистрация
-
Последен вход
-
Days Won
50
Content Type
Профили
Форуми
Библиотека
Articles
Блогове
ВСИЧКО ПУБЛИКУВАНО ОТ gmladenov
-
Боби и Васил са в покой, така че дори да са натрупали разлика, те могат да си синхронизират часовниците. Не е там проблема. Проблемът е, че двама наблюдатели в покой един спрямо друг имат различни времена. Подобна постановка няма смислено обяснение.
-
Здравейте, В тази тема ще показа поредния парадокс на Специалната Теория на Относителността (СТО), който съм наименувал Парадоксът на тризнаците. Той показва как според СТО времето на два наблюдателя е различно дори когато те са в покой един спрямо друг и "делят" една обща отправна система. Това, разбира се, няма никакъв физически смисъл. Примерът с тризнаците Ана, Боби и Васил са тризнаци. Един ден Васил се отправя на космическо пътуване със скорост v=с/2, докато Ана и Боби остават на земята. Но след точно една година, Боби поема по същия път като Васил. Полетният план на Боби е идентичен с този на Васил, така че той се ускорява до оперативната скорост v=с/2 точно една година след Васил и също като него започва да се движи инерциално. От този момент нататък двамата се намират в покой един спрямо друг, докато едновременно с това се движат спрямо Ана. Тази постановка е показана на долната илюстрация. Тъй като Боби и Васил са в покой един спрямо друг, те се намират в една обща отправна система, която се движи спрямо отправната система на Ана. За удобство приемамаме, че началата на двете системи съвпадат в момента когато Васил достига оперативна скорост и започва да се движи инерциално. Така една година по-късно, когато Боби сторва същото, Васил се намира на половин светлинна година разстояние от Ана. Нека сега да приложим Лоренцовата трансформация и да изчислим времената на Боби и Васил спрямо Ана. Формулата за превеждане на времената е както следва (γ е коефициентът на Лоренц): За четливост на сметките дефинираме константата Ψ (пси), която се равнява на броя секунди в една година: Ψ = 365*24*60*60 Замествайки в Лоренцовата формула, получаваме: tБ' = γ(t-0) = γ(Ψ-0) = γΨ tВ' = γ(t-vvt/cc) = γ(Ψ-Ψ/4) = γΨ(3/4) Δt' = (tБ'-tВ') = γΨ/4 Както се вижда, времената на Боби (tБ') и Васил (tВ') са различни ... в една и съща отправна система, в която и двамата са в покой. За да сме сигурни, че не сме допуснали грешка, нека да изчислим времената след 10г пътуване. През това време Васил е изминал 5 светлинни години разтояние в системата на Ана, докато Боби е изминал 4,5 светлинни години: tБ' = γ(t-vvt/cc) = γ(10Ψ-9Ψ/4) = γΨ(31/4) tВ' = γ(t-vvt/cc) = γ(10Ψ-10Ψ/4) = γΨ(30/4) Δt' = (tБ'-tВ') = γΨ/4 Времената на двамата отново са различни, но разликата между тях се запазва същата както и в горните сметки. Коментар СТО ни учи, че отправни системи, намиращи се в движение една спрямо друга, имат различно време. Но "вътре" в една отправна система времето е еднакво за цялата система. Както се оказва, обаче, последното в същност не е вярно. Горният пример с тризнаците показава отправна система, в която има две различни времена. А ако се вгледаме по-внимателно ще установим, че според СТО всеки преведен х-координат в подвижните системи има свое собствено време. Това, разбира се, е физизеският безсмислено. Как измерваме, например, разстоянието между Боби и Васил горе, ако всеки от тях има свое собствено време? Въпросното измерване изисква едновременност между двамата, а според СТО такава няма ... въпреки че те са в покой един спрямо друг. Значи според СТО излиза, че разстоянието между Боби и Васил е неизмеримо. Нещо друго. Докато времето в отправната система на Ани е еднакво в цялата система, времето в системата на Боби и Васил очевидно не е такова. Това веднага повдига въпроса защо СТО използва двоен стандарт за отчитане на времето в двете системи - и най-вече защо го прави без каквото и да било обяснение? Нима използването на двоен аршин в различните системи е нещо, за което не си струва да се говори в една научна теория? Това са принципните въпроси, които парадоксът с тризнаците повдига ... и те естествено са реторични въпроси, защото нищо не оправдава използването на двойни стандарти в една точна наука, каквато е физиката. Манипулациите на времето, които СТО извършва, са просто стъкмистика, с която скоростта на светлината излиза еднаква във всички отправни системи. Те нямат нищо общо с реалността. Благодаря за вниманието. Георги Станимиров, програмист ©2020, всички права запазени
-
Добре, но кой от двамата наблюдатели увлича подвижното пространство? Ако ти разбирам правилно идеята, пак се опира до това, че трябва да знаем кой от двамата е подвижен и кой е стационарен. Без това знание не може да кажем кой увлича пространството.
-
Да ... но класическата механика се ограничава само с механично инерциално движение, без да включва електромагнетизма (ЕМ). СТО е тази, която обедениява механиката и ЕМ - но СТО приема, че движението е неоткриваемо с ЕМ експеримент. В момента във физиката няма класическа трактовка, която да обединява механиката и ЕМ ... но която също така да приема, че движението е откриваемо с ЕМ експеримент. Етърната теория на Лоренц би трябвало да е такава, но тя не е актуална.
-
Става това, че като си завреш главата между задните части, почваш задаваш ей такива въпроси.
-
Да, точно това е. Причината СТО да изисква материална отправна точка е неоткриваемостта на движението. Щом не можеш да определиш дали се движиш или не, тогава ти трябва материално тяло, спрямо което да отчиташ промяна на разстоянието. Но ако приемем, че движението е откриваемо ... по начина, по който Майкелсон и Морли са искали да го открият на времето ... тогава отправната точка вече не е задължително да е материална. Мястото в празния космос, където избухва една свръх-нова, е (теоретически) възможно да се триангулира дотогава, докато все още има светлина от нея ... по силата на това, че светлината от свръх-новата се разпространява с изотропна скорост. Значи това място е определимо/намираемо и фиксирано докато все още има светлина от свръх-новата. А щом това е така, то може да служи за отправна точка. Така в крайна сметка откриваемостта на движението чрез светлината е условието, което определя дали можем да използваме нематериални точки в пространството за отправни точки. В СТО това условие не е изпълнено, така че такива отправни точки не може да има. Но ако приемем движението за откриваемо (чрез светлината), тогава може. Диполната анизотропия е доказателството, че движението е откриваемо чрез светлината.
-
Не знам защо ти се губи идеята какво е относително движение, както е дефинирано според СТО и релативизма. Според СТО не можеш да се движиш спрямо картина от миналото. Изисква се материално тяло, за да можеш да измериш промяна на разстоянието спрямо него. А разстоянието до "картина от миналото" не може да бъде измерено. Така че се осъзнай малко. Да, диполната анизотропия наистина е движение спрямо картина от миналото ... но такова движение е невалидно според СТО. Ти това не проумяваш. Въпросът не е да намериш каквато и да било отправна точка, а отпрвна точка, която е валидна според критериите на СТО и релативизма.
-
За пореден път: диполната анизотропия какво е? Ти прочети ли го този постинг. Доста е образователен.
-
Физиците от 19-ти век искат да свалят Нютон от сцената, защото според тях неговата вяра в Бог е ненаучна. И толкова държат на това, че сега сме в другата крайност ... да вярваме в СТО, въпреки очевидните и грешки и парадокси. Вече не сме в 19-ти век и е време физиците да не се плашат от Бог, а да гледат коя теория отговаря на действителнистта. Кое е по-добре: грешна теория, създадена от атеист - или вярна теория, създадена от вярващ ??
-
Нютон казва: ... ние трябва да се абстрахираме от нашите сетива и да раглеждаме нещата сами по себе си, оделно от нашите сетивни мерки за тях. Смисълът на този цитат е, че трябва да гледаме в същината на нещата - а не само в това, което измерваме. Значи Нютон изрично казва, че ние използваме относителни мерки за местоположения, разстояния и движение - но призовава да гледаме същината на нещата.
-
Такова животно нема !! Точно така. Не. Това означава, че ако ти можеш да откриеш собственото си движение, тогава нямаш нужда от отправна точка, за да кажеш, че се движиш. Както искаш го наречи това движение - абсолютно, собствено и т.н. - но фактът е, че ти можеш да определиш скоростта си на движение без отправна точка. Диполната анизотропия го показва, както и твоят пример с галактиките.
-
Ами точно. Щом галактиките ги няма, ти спрямо какво се движиш? Кое разстояние скъсяваш или удължаваш, ако галактиките вече ги няма? Ти самият ми даваш пример за това, че се движиш без отправна точка ... след което ми казваш, че всяко движение е относително.
-
В известана Принципия Математика: https://archive.org/details/newtonspmathema00newtrich/page/n81 В точка "II" на страница 77 Нютон казва: Абсолютното пространство, по природа и без отношение към нищо външно, остава винаги подобно и неподвижно. А в точка "IV" на следващата страница Нютон казва: Абсолютно движение е преместването на едно тяло от едно абсолютно място на друго. Така че когато се говори за Нютонова физика трябва да се знае, че абсолютното пространство е неподвижно, а абсолютното движение е преместването на едно тяло в абсолютното пространство. За отправни точки тук въобще не става дума. Естествено в Нютоновата физика също така има и относително движение, за което вече се изисква отправна точка. Абсолютното движение, обаче, не е спрямо каквото и да било, а е просто преместване в абсолютното пространство.
-
Хехе, ти току що обясни защо СТО греши да изисква отправна точка за движение. За стотен път: това се изисква, защото според СТО и релативизма инерциалното движение е откриваемо единствено по промяната на разстоянието между две тела. Иначе то е неоткриваемо. Именно затова ти трябва материално тяло за отправна точка, за да можеш да измериш промяната в разстоянието (която принципно се смята за измерима).
-
Ако движението задължително трябва да е спрямо нещо, тогава си прав. Но аз съм с Нютон, че движението е просто преместване и не е необходимо да е спрямо нещо.
-
Спрямо какво избираш началото на координатната система, майна? Нали проблемът е, че трябва да можеш да измериш промяна на разстоянието между две тела? Ако избереш произволна точка в космоса за начало на отправната система, как отчиташ промяна на разстоянието до тази точка? Аз винаги съм твърдял, че вакуумът на космоса може да служи за отравна система ... което се оспорва с аргумента, че според СТО за отправна система задължително трябва материално тяло. А сега се оказва, че това не било задължително. СТО явно се майтапи.
-
За близък източник да, ама за далечна звезда?? Нали затова имаме Полярна звезда: както и да се движиш, тя винаги се пада на север. Значи как определяш скоростта си на движение, ако знаеш само какъв ти е ъгъла спрямо Полярната звезда? Ако обяснението на Брадли за зездната аберация беше вярно, тогава наистина щеше да е възможно да си изичслиш скоростта си на движение. Само че обяснението на Брадли не е вярно.
-
Има разстояние до началото на координатната система. Ако не си чул, викат му координат.
-
А така. И колко е разстоянието от спътниците до източника на реликтовото излъчване?
-
Точно така, може ... но според СТО/релативизма не може. Според СТО движение има само ако има промяна на разстояние. Такава промяна спрямо реликтовото излъчване не може да бъде отчетена. Как ще измериш такава промяна? Значи СТО бърка, че движение без промяна на разстояние няма. Затова диполната изотропия оборва СТО. Тя ти дава скорост и посока на движение в космоса без отправна система ... което според СТО е невъзможно без да си избрал материално тяло за отправна система, спрямо което да отчиташ промяната на разстоянието.
-
Ъглите не помагат да разбереш каква ти е скоростта. Това се разбира само по промяната на разстоянието до друго тяло.
-
Ти не си казал три перпендикулярни една на друга посоки, а три различни посоки.
-
Именно. Тогава как избираме началото на отправната система на реликтовото излъчване?
-
И как отчиташ промяна на разстоянието до реликтовото излъчване? Кой закон на Скенеровата физика използваш??
-
Това е точно така и един триизмерен (3D) импулс ти го дава. Не просто три различни посоки, а всичи различни посоки.