Станислав Янков
Потребител-
Брой отговори
2763 -
Регистрация
-
Последен вход
-
Days Won
1
Content Type
Профили
Форуми
Библиотека
Articles
Блогове
ВСИЧКО ПУБЛИКУВАНО ОТ Станислав Янков
-
Аз ще вървя, но съм сигурен, че няма да одобрите посоката. Изглежда ми, сякаш идеализираните философски и математически абстракции са взели връх над реалните разсъждения и в някои случаи може би са стигнали прекалено далеч. Като в случая с идеализираната часовникова абстракция, където сякаш се има предвид не просто идеален часовник, с идеален механизъм, който отчита идеалното-точните времеви интервали, а съвсем безструктурен такъв, който "съобщава" идеалните параметри магически. Така че - вероятно има още къде надолу да копая...
-
Последен въпрос: Защо се счита, че при разглеждане на реален часовник и неговите части, той може да влияе на резултатите? С неговата синхронизация по еталона той отговаря на идеализираната абстракция (но си го има реално, както и движенията на неговите части в пространството). Самият часовник и неговите части са повлияните от особеностите на пространствената (пространствено-времевата) геометрия при движение на две инерциални системи с някаква скорост една спрямо друга.
-
"Освободените" чрез тези абстракции неща не престават да съществуват реално и не би трябвало употребата на подобни абстракции да се ползва като забрана на пълно разглеждане на реалната основа, от която произлизат! Благодаря за коментарите ти, насочиха ме към неща, които досега считах за подразбиращи се, а всъщност крият интересни детайли, на които не обръщах достатъчно внимание. На Гравити, Кипен и Шпага също благодаря, ще опитам да намеря време за по-внимателно вникване във възражението на Гравити относно Евклидовата специална относителност. Чао засега!
-
Аргументът на Скенер, че оня въпрос, който задавам, е некоректен се състои в това, че не ползвам микс между абстрактните философски същности (в конкретния случай - тази на часовниковия темп) и конкретните времеви показатели. Един вид, че като обявим синхронизирания с еталона реален часовник за философска абстракция - той вече няма значение и едва ли не престава да съществува. Така наистина няма как да покажа, че извъртането на примовите координати към диагонала на светлинната скорост в диаграмата на Минковски (това, че трансформациите са Лоренцови, а не Галилееви) може да се опише и чрез четири реални пространствени измерения, а не единствено чрез пространство-време. За целта ми е нужен анализ на реалните часовници и движението на техните части в пространството. Както и да е! Смятам малко да си почина, както ме беше посъветвал Скенер, физиката не е единственото занимание в живота ми! Приятни моменти за всички, докато не се включа пак! И само едно бързо уточнение - философията е ключов дял от науката, нейното подценяване не е смислено!
-
Проблемът ми в този случай е, че не съм съвсем сигурен, че Гравити тълкува напълно правилно детайлите на подхода. Струва ми се, че той (и не само той) прибързва, с няколко бързи контра-аргумента да отрече всичко. А в момента аз просто не разполагам с нужното време, за да изследвам и това нещо в нужната дълбочина. По-натъка, при възможност, задължително ще видя, това ми е интересно и на мен, но сега просто нямам време!
-
Вероятно да, но разривът в случая е същностен - вие отдавате по-важен приоритет на нещо (изчистените философски абстракции), което не би трябвало да е приоритетно, а минимум равностойно на според мен по-близките до реалността, по-непосредствените фактори (настроените реални часовници и конкретните времеви показатели, които се ползват във физическите изчисления). Абстрактните философски есенции произхождат от по-близките до реалността същности (конкретните параметри и реалните часовници за извличането на конкретните параметри), като се отстраняват техните "израстъци" ("режат се космите") и така се извлича същността в основата. Но все пак всичко се базира на физическата реалност и на реалните регистрации на параметри, нали? Ако приемем фундаменталните философски същности за по-важните, така допускаме да са по-важни от регистрациите на реалните параметри, на чието "орязване" всъщност се базират.
-
Разбрах какво става! Причината да не се разбираме е, че редим по различен начин приоритета на петте компонента физическа реалност, конкретен времеви параметър, реален часовник, времева философска (фундаментална) абстракция и идеализирана часовникова абстракция. Според мен последователността е физическа реалност (водещият играч в цялата тая игра), конкретния времеви параметър + реалния часовник, чрез който се извлича въпросния времеви параметър и чак накрая е философската есенция на всичко това, получена чрез „орязването“ на подробностите от конкретния времеви параметър и от реалния часовник – базовата (философска) времева абстракция + идеализирания, абстрактен часовник (до който се достига чрез настройването в материалната реалност на реалния часовник до общоприетия времеви еталон – без такова настройване реалния часовник може да има компоненти с всякакви особености и да извежда произволни материални темпове накрая, което не позволява да се дефинира като споменатия идеален, абстрактен часовник). Според вас физическата реалност също е водещата, но след това следват абстрактните време и часовник и чак накрая е конкретния времеви параметър, докато реалния часовник направо може и да го няма и това е подредбата, чиято логика аз не успявам да разбера. Според мен по-ключов е онзи елемент, който е по-близо до физическата реалност – конкретния времеви параметър + настроения по еталона реален часовник, чрез който въпросния времеви параметър се извлича. В крайна сметка, за да се получат идеализираните, абстрактните философски есенции на време и часовник – трябва преди това да има по-обхватните и пряко свързани с физическата реалност компоненти (конкретния времеви параметър + настроения реален часовник), чиито подробности да се „орежат“ (да се отстранят космите им, както се изрази по-напред Скенер) и по тоя начин да се достигне до философската им същност, нали? Защото ако орязаните абстрактни същности в основата са по-важните, тогава лесно може да се достигне до положението със суперструнната теория, където съществуват някои изцяло теоретични и неподкрепени с реални същности детайли. В ситуацията с абстрактните време и часовников темп всичко си е наред и напълно коректно, за разлика от някои подробности около суперструнната теория, защото абстрактните време и часовников темп разполагат с ясно дефинирана материална наличност, пряко свързана с физическата реалност – конкретния времеви параметър за абстрактното време и настроения по еталона реален часовник за абстрактния часовников темп.
-
Тоест - проблемът, който визира Гравити, е от алгебрично естество ли? Ако видя сравнение на изчисления по двата начина, ще разбера, но за да търся, трябва да съм сигурен, че проблема е в алгебрата (времето ми е доста оскъдно, за да търся без причина), тоест - че формулите не съвпадат напълно с диаграмата, която няма проблеми. Защото като диаграма - всеки от двамата близнаци си има собствена диаграма на Епщайн в покой, както си има и собствена диаграма на Минковски в покой, а другия близнак, който е считан като подвижен, е с различните параметри, точно като при диаграмата на Минковски. И при срещата диаметъра (координатното време на подвижния близнак) просто се завърта нагоре (както се завъртат примовите t и х на движещия се близнак, който е считания за такъв, при Минковски) и си съвпада с сTau, когато и двамата са в покой един спрямо друг. Практически всичко, като диаграми, е едно и също и резултатите на променените дължина и часовников интервал са същите като от Лоренцовите трансформации.
-
ОК! Говориш за покоя! Вече го разбирам! Прав ли съм в представата си (тя е формирана още някога, при обсъжданията ти с Младенов на абстрактните особености на времето), че докато конкретизирания времеви параметър t (конкретното материално устройство на часовници) включва практическите подробности, то абстрактната философска дефиниция на времето (и на идеализираните часовници - това е добавка от настоящата дискусия) се занимава само с по-общите, принципни контури на понятието "време" (и "часовник") във физиката, без специални конкретизиращи детайли? И че дори и така, ако практическите регистрации на подробностите около времето налагаха някаква по-различна обща (абстрактна, философска) представа за времето (и часовниците) в сравнение с настоящата - съответните промени щяха да бъдат наложени на общата картина (царят е практиката, а не мисловните ни модели, колкото и фундаментални неща да разглеждат тези модели)?
-
Защото започвам леко да се обърквам! Виж какво си написал тук и какво си написал по-рано: Още преди години се дискутираше тук философското понятие за време и че има време (подобно на температура, налягане, цвят...) като обща, философска абстракция, без конкретни параметри и след това е времевият параметър със съвсем конкретни характеристики, който се ползва за физическите изчисления. Явно и часовникът като принцип има подобна обща абстракция, като общата на времето, чак след което идват конкретните му конструктивни характеристики, чрез които се изпълнява общоприетия времеви еталон. И аз неколкократно по-назад споменах, че имам предвид не общата абстракция "време" ("температура", "налягане", "цвят"...), която е нещо подобно на Платоновия математически свят на Пенроуз, а имам предвид съвсем конкретния параметър време, който се получава чрез конкретен часовник с материален темп в пространството, настроен по общоприетия еталон. Общата абстракция не я разглеждаме (както времевата, така и часовниковата, след като и тя има подобно изражение), разглеждаме само конкретиката и начина на нейното получаване в действителността. В действителността не можеш да получиш часовников темп без реално материално устройство, с реално движение на негови части в пространството, което да е настроено по общоприетия еталон. Дори повече! В естествената реалност, не във философската област, абсолютно всяка регистрация на последователност преди-сега-после се основава на някаква материална динамика в пространството, даже и разни неща да изглеждат привидно неподвижни. Без някакви движения на материя в пространството, минимум под формата мозъчни процеси ("часовника" на съзнанието), не би могло да се получи усет за последователност преди-сега-после. И специално беше подчертавано във форума преди някакво време, че усилия на Пенроуз да обоснове квантово-механични процеси във връзка с работата на мозъка (процеси "извън" материалната динамика в пространството) са се провалили (били са категорично опровергани). И сега - ясно сме споменали, че нямаме предвид общите абстракции (Платоновия свят във връзка с времето), боравим само с практическите показатели от ежедневието. И ти споменаваш горните две неща! Това започва да ме обърква, защото така би излязло, че освен общата абстракция за време и конкретния времеви параметър от ежедневието, който се ползва във физическите изчисления и се получава от реални материални движения в пространството, сякаш има и някаква промяна като движение на материята извън пространството, извън пространствените координати, която също участва по някакъв начин в оцифровяването на времевия параметър от ежедневието. Това нещо не успявам да си го изясня какво е и откъде идва. Някаква допълнителна дефиниция на времето ли има, освен общата абстракция и практическата употреба?
-
Ти ме прати към страниците назад, когато губих време да обяснявам, защо не успявам да разбера аргументите ти там. Само сравни колко съм изписал аз и какъв е твоя отговор! Изглежда само когато Скенер пише по много, това е сериозно усилие, а когато го прави някой като мен - това е без значение, защото аз пиша пълни глупости... Дал съм ти няколко отговора на твоя въпрос по-назад - виж ги, няма смисъл да се повтаря по сто пъти едно и също нещо.
-
Струва ми се, че тук се засяга дълбок философски въпрос, което ще рече - самия фундамент, базовите логики. Затова и се посипва чак такъв порой от възражения срещу мен. За да можем да кажем, че има промяна без движение, трябва да демонстрираме ситуация, в която реално присъства подобна промяна, без да съществуват пространство и от там и движения в такова пространство. Това е необходимо, за да се потвърди без никакви съмнения, че такава промяна е въобще възможна принципно. Има ли такава ситуация? Ако не може да се демонстрира промяна в отсъствие на пространство и от там и отсъствие на движение в такова – значи всъщност покоя (една от особеностите на подобна промяна без движение в пространство) е илюзия, просто "замъгляване" на разни материални движения в пространството, които не сме в състояние да регистрираме сетивно. Когато ни изглежда, че стоим на място спрямо някакви неща – в точно същия момент спрямо други неща се движим и всичко се състои в това, да определяме спрямо кои неща с каква скорост между 0с и 1с се движим. Нещо повече – самите неща, които само ни изглеждат неподвижни спрямо нас, всъщност постоянно трептят. Атомите на всичко непрекъснато трептят, макар масивните неща, които изграждат, да ни изглеждат неподвижни (просто не сме в състояние да регистрираме постоянното движение, свързано с тях и тук светлината, като медиатор между нас и наблюдаваните други обекти, играе ключова роля). Движението е НАВСЯКЪДЕ И НЕПРЕКЪСНАТО! Промяната и движението в пространството са неразривно свързани едно с друго и представляват обобщението, а покоят е техен частен случай, условност, заради невъзможността да регистрираме някакви движения. Това е базата на всички следващи мои разсъждения и като че ли това е причината да не успяваме да се разберем – представата за времето и неговите интерпретации сякаш се базират на възможността за протичане на промени в покой, извън движението в пространство, а това според мен е невъзможна ситуация, която не може да присъства реално, само условно. Има и нещо друго! Ако приемем възможността да съществуват материални промени извън пространството и материалните движения в него, много лесно след това ние можем да приемем, че тези външни за пространството материални промени може да са в големи мащаби и от там крачката към приемането на реалното наличие на различни светове извън нашата реалност (разни религиозни описания на Божествени светове) е само една... Това ми бяха съображение да ти пиша по-рано, че сякаш става дума за случването на някакви неща в НИЩОТО и че това прилича на религиозен подход, не нещо си да ти се подигравам или просто за да ти противореча.
-
Аз не разбрах, защо да не е координатна система. Координатната система е система в геометрията, която използва числа, наричани координати, за да определи еднозначно положението на точките или на други геометрични обекти в дадено пространство или по-общо – в дадено математическо многообразие. Координатите на дадена точка могат да бъдат различни геометрични величини, като обикновено те са разстояния от точката до определен обект или ъгли между радиус-вектора на точката и определен обект. Координатните системи могат да бъдат всякакви, включително афинни, криволинейни, полярни, сферични, цилиндрични... Както всеки отделен обект (инерциална система) си има собствена диаграма или конус на Минковски, за собствения покой, така и всеки обект може да си има собствена диаграма на Епщайн за собствения покой. В едно общо изображение могат да се дадат множество отделни конуси на различни обекти (следващото изображение е във връзка с друго нещо, но не искам да товаря форума с излишни изображения и ползвам стари в други връзки, където мога). По същия начин могат да се ползват и множество отделни диаграми на Епщайн за отделните обекти. Както при Минковски диаграмата може да се разшири до конуси, за да показва повече, така и диаграмата на Епщайн може да се разшири до сфера. Параметрите t и х в диаграмата на Минковски се наричат координати и няма причина параметрите в диаграмата на Епщайн също да не се наричат координати. Въпрос на развитие на епщайновия подход, който сега е меко казано недоразвит! Не успях да разбера ясно обясненията ти на тези две страници и какви са възраженията ти, защо диаграмата на Епщайн да не е с координати, докато тая на Минковски да е с координати!
-
Защото видимо се заяждаш. Почти не разясняваш нищо, а само питаш, сякаш някъде съм казал, че знам всичко и всичко е готово. Щом знаеш, че някъде греша и не желаеш да кажеш къде (например, защо параметрите на изображението на Епщайн да не са координатна система, след като понятието "координатна система" е доста общо и може да се ползва за много неща, не само за пространство, нито само за скорости) - дръж си го!
-
Не си ли го казал?! Това, дето ще цитирам, от кого е написано: "Има много проблеми и недостатъци." (стр. 181). "Това не е координатна система." (стр. 182, специално за диаграмата на Епщайн, където двете перпендикулярни оси са х и сТау и няма какво друго да са, освен оси на координатна система, при това на системата на Минковски, гледана "отгоре", а диаметъра е времевата координата на подвижната инерциална система и се завърта с промяната на скоростта ѝ спрямо неподвижната, точно както се завърта примовата времева координата на подвижната система в диаграмата на Минковски и е така, защото това е точно същата тази координата). И т.н. Да ти цитирам ли още по-стари твои коментари, където директно казваш, че подхода на Епщайн е неверен?
-
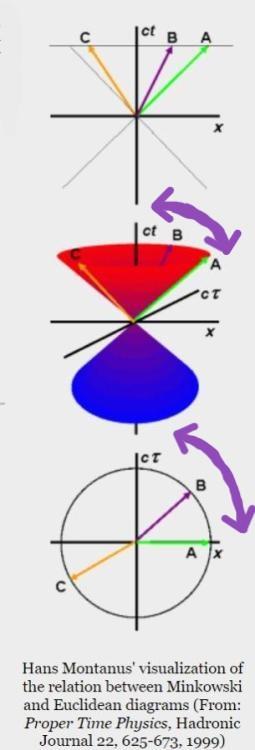
Защо ти не обясниш малко по-подробно, как подхода на Епщайн не е верен, макар да дава точно същите резултати, като от Лоренцовите трансформации и напълно да се базира на диаграмата на Минковски, просто "наблюдавана завъртяна"? Какъв, малко по-подробно, е този проблем във връзка с употребата на собственото време Тау на подвижната система, който ти смяташ, че има? Някакъв алгебричен ли е? Защото диаграмен не може да бъде - кръгът от диаграмата на Епщайн е върха на конуса на Минковски, когато х е равно на 300000 км, а сТау е равно на една секунда, завъртането на виолетовата стрелка В (координатното време Т от диаграмата на Минковски) е ъгъла на примовите координати на движещата се инерциална система от диаграмата на Минковски и въобще - абсолютно всичко, налично при диаграмата на Минковски, го има и при диаграмата на Епщайн, само е представено различно, "завъртяно". Какви неверности може да има тук при това положение?
-
С какво Хамилтъновата механика е по-добра от Лагранжовата механика, та са разработени и двете, вместо само едната? Единственият въпрос е - дали подход с четири пространствени измерения дава верните резултати или не и ако дава верните резултати, значи има смисъл да се разработи. Неслучайно се разгаря чак такъв спор с мен именно относно верността и коректността на такъв подход, не просто относно ползата и смисъла от него. В никакъв случай не ги приравнявам и това е един от упреците - предлагам промени в самата метрика (базовите параметри на матрицата на метричния тензор, тези по диагонала) и така сякаш нарушавам употребата на четири еднакви координати от стандартната пространствено-времева концепция. Линийките (и лазерите, както и всички други пособия за мерене) също са материални устройства, подобно на часовниците. Надявам се такъв подход да предложи по-еднородно описание (всички измерения са с еднакво естество, пространствени, само числовите параметри във връзка с тях са различни) и така да е по-лесно съчетаем с всичко останало (забележи, че по никакъв начин не отрича например СТО и ОТО, само интерпретира по различен начин същите резултати). Защото скоростта е параметъра, чрез който се определят разликите в параметрите между различни инерциални системи в движение една спрямо друга, скоростта се свързва с движение в пространство, това е геометрия и значи, че има геометрични причини, свързани с пространството (с пространство-времето при интерпретацията 3D+1D), които водят до регистрираните различия при движещи се една спрямо друга ИОС. Иначе времето щеше да е абсолютно и щяха да са валидни Галилеевите трансформации. Няма значение кой е съгласен или не, това не е политика, от значение е само дали е вярно или не. Ако не е вярно - просто няма да ми се получат усилията (но ще съм научил още полезни неща, както научих и от последните коментари на Скенер, а и ти вече слагаш някои полезни неща, не е като изявите ти от някога).
-
Нужни са часовници (и в двете инерциални системи), които да са достатъчно точни. Практически забавянето на хода на часовниците при достатъчно бързо движение (на самолети, космически апарати и сателити) се регистрира, съвсем реално, чрез атомни часовници (възможно най-точните налични). Имай предвид, че за принципно обсъждане на въпроса не са нужни свръх-точни часовници и нещо повече - наличието на каквато и да било промяна на каквото и да било, която си в състояние да регистрираш в последователност едно след друго, условно се явява часовник (например - прелитане на птичка и произволен момент СЛЕД ТОВА да се спънеш, докато си ходиш по улицата). За регистриране на времеви ефект са необходими две неща - някакви регистрируеми материални промени, все едно какви, стига да могат да се регистрират и да не се случва абсолютно всичко едновременно. Принципно абсолютно всичко, без изключение, представлява абстракции, даже и религиозните абстракции претендират да включват някакъв вид практически потвърждения, при научните абстракции проверките и потвържденията са многократно по-стриктни и точно затова при последните можем да говорим за в значителна степен реални параметри.
-
Ще прегледам отново всичко, което си написал в тази връзка, само имай предвид, че нямам проблем да приемам неподвижност в пространството като част от пространствено-времева парадигма и е ясно, че това нещо си идва още от класическата механика. Единствено, това с промяната като несвързана с движение в пространство не ми се връзва с неизбежната нужда от часовниково устройство дори при самата неподвижна система, без още да са започнали каквито и да било сравнения с други системи. Ние самите, нашата съзнателност, имаме часовниково устройство – мозъка. Стрелата на времето, ентропията, която я причинява, е неразривно свързана с движение на материя в пространство. Иначе какво и как ще се разрежда ентропийно все повече, за да формира така Стрелата на времето?!
-
Това сравнение е последващо, между инерциални системи, които се движат. Аз имам предвид, че при самата неподвижна система трябва да има втора инерциална система в движение с някаква скорост в пространството (цикличности, еталони, правила - подробности), часовниковото устройство, която да служи за числово остойностяване на времевия параметър и без това не можем да дефинираме подобен параметър и от там не можем и да правим сравнения между времеви темпове на различни инерциални системи. Часовниковото устройство съвсем не е абстрактно, то е реално. Скенер казва, че промяната е нещо отделно от движението, по-важно от движението, може да я има и без движението, а движението е само неин частен случай.
-
Проблемът е на още по-ранен етап и заради това аз не успявам въобще да стигна до опит да аргументирам това, което си представям като връзка. Ти отделяш времето като някаква по-специална категория, която има свое собствено, самостойно и по-важно значение извън числовото ѝ остойностяване, което може да стане единствено чрез употребата на материално движение в пространство (там цикличностите и все по-сложните часовникови конструкции за все по-голяма прецизност са периферни подробности, които само биха замъглили принципните разсъждения по въпроса). На мен ми се струва, че след като не съществува възможност за повече или по-малко точно числово остойностяване на времеви темп (без такова остойностяване не можем да правим никакви физически сравнения и принципно такова остойностяване, макар и твърде неточно, е и разграничението сутрин-обед-вечер и всяка друга причинно-следствена последователност с някакъв темп в пространството) – материалното движение в пространството е вложено като неразделен елемент от физическата представа за време. Ако промяната е нещо различно и отделно от движението на материята в пространство, тогава – промяна на какво и по какъв начин?! Ето това не успявам да разбера!
-
Изглежда голямото разминаване е в оценките ни на това – кое е причина и кое е следствие, кое е водещо и кое последващо. Подобни са и въпросите на Гравити – защо движението да било важно колкото времето, след като не може да се обоснове без времеви параметър. Аз разглеждам движението в пространството, отстоянието на пространството и времевите параметри като равностойни, не като някое да е по-важно от другото. Няма никаква пречка едновременно да си наблюдаваме движението на часовниковите части в пространството (нека да е най-прост часовник, с махало, защото тук не обсъждаме качествата на устройството, а принципите в основата на отмерването на времето) и същевременно да ползваме часовниковите показатели за оценяване на различните скорости на различните части на часовника (включително и на онези часовникови части, които са в покой спрямо наблюдателя) и цялата игра е в точното определяне на наблюдател-наблюдаемо (покояща-подвижна система). И от тука аз твърдя, че можем да съставим напълно еквивалентна на пространствено-времевата, изцяло пространствена концепция с четири пространствени измерения, вместо с три пространствени и едно времево, а вие твърдите, че може да е вярна само пространствено-времевата концепция и другата не може да е вярна. Изглежда ми, че това е нещото, относно което не можем да се разберем и трябва да се разчопли по-задълбочено!