Станислав Янков
Потребител-
Брой отговори
2763 -
Регистрация
-
Последен вход
-
Days Won
1
Content Type
Профили
Форуми
Библиотека
Articles
Блогове
ВСИЧКО ПУБЛИКУВАНО ОТ Станислав Янков
-
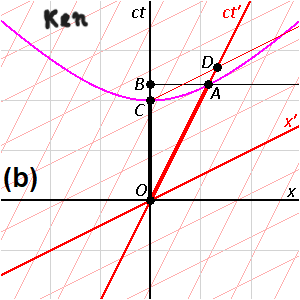
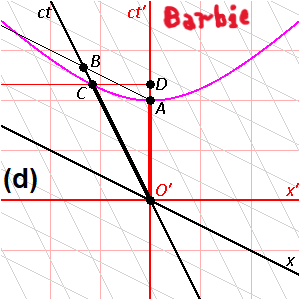
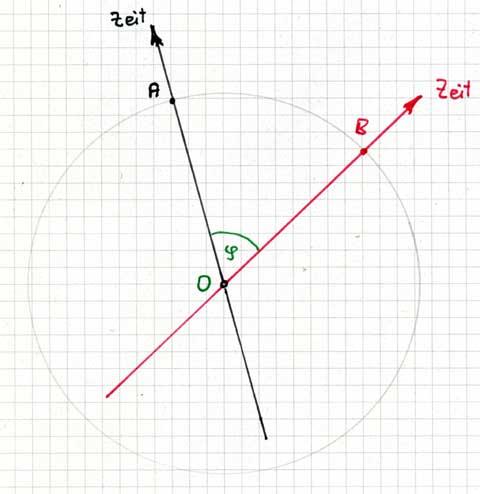
Ето как четвъртото пространствено измерение w се представя чрез пространствено-времевите диаграми на Епщайн (кръгово завъртане между основната и примовата координатна система) и на Минковски (хиперболично завъртане между основната и примовата координатна система). Разликата асиметрията) между мащабите на пространственото отстояние по направлението на едната от четирите пространствени координати спрямо останалите три координати се дължи на макроскопичното (3D) естество на функционирането на човешкия мозък. Ситуацията е много подобна на тази със зрението, където 3D-пространствена околност се наблюдава през 2D-пространствен "екран" (само широчина и височина) и дълбочината се характеризира посредством проективни техники (основно - стереографска проекция). Всяка от различните инерциални отправни системи се характеризира от собствено пространство. Има условия, при които пространства на инерциални отправни системи (тези, при които посредниците на взаимодействията могат да достигнат съответните им обекти) могат да взаимодействат едно с друго (включително да се наблюдават посредством светлината, която е електромагнитното взаимодействие) и има други условия, при които не могат да взаимодействат едно с друго. Времето при 4D-пространствената концепция не е измерение, то е просто параметър, както дължината и макар да е абсолютно само по себе си, както дължината (употребяват се идеални часовници и линийки за замерванията), то също така е и относително, както и дължината, заради регистрирането на 4D-пространствена реалност през 3D-призма. Естеството и особеностите на времето не могат да намерят отговор при СТО и ОТО, отговорите във връзка с времето и неговата стрела се намират някъде на квантово равнище и по-специално - при квантовата гравитация.
-
Не-не! Не се напрягай, това е занимание от любопитство и за удоволствие, не някаква битка или съревнование. Само неща, които ти хрумнат на момента, без усилие и ако ти е приятно да отговориш. Аз имам предвид следното: Дали ще приемеш директно времето за условно измерение и ще станат четири измерения или ще опиташ някаква геометрия с четири пространствени измерения - и в двата случая съществува подобна асиметрия между едното и трите измерения. По времето не можеш да се връщаш назад, както можеш при трите пространствени измерения, а при вектора със скорост 1с в четиримерно пространство съществува привилегирована посока в обема на четиримерното пространство (тази на вектора), където е и максималната степен на пространствено съкращение. Това е безспорно асиметрична ситуация, отговорът за наличието ѝ се крие някъде в гравитацията и при това на квантово ниво - сега не се занимаваме с това. Дали ще осъществяваш хиперболично въртене на координати през конусите на Минковски, когато директно времето е измерението или ще осъществяваш стандартно кръгово въртене на скоростов вектор в четиримерно пространство (това въртене не може да надхвърли 90 градуса, защото четвърта пространствена координата w се разполага на 90 градуса от всяка от останалите координати х, у и z), резултатите ще са подобни в 3D+1D txyz и в 4D wxyz и ще са еднакви в 3D xyz (Лоренцовите трансформации) - съкращаване на дължината по посоката на движението х и удължаване на времевия интервал по времевата координата t в 3D+1D или съкращаване на дължината по посоката на движението х и удължаване на дължината по четвъртата координата w с извъртането на скоростовия вектор в 4D-пространството wxyz. И в двата случая могат да се изведат всички особености на СТО, аз в момента не мога да открия какво във втория случай (4D) може да наруши принципите на относителността, като и в двата случая стои въпрос за решаване в по-фундаменталните области - защо времето е условно измерение и не можем да се връщаме назад по него при пространство-времето и защо съществува привилегирования вектор 1с със само една конкретна посока при четиримерното пространствено разглеждане. Това, че в случая има нужда от идеално-точни часовници и линийки не значи, че има нещо абсолютно - времето е просто параметър (не измерение), който произтича от особеностите на 4D-пространствената геометрия точно така, както произтича от същите особености и дължината по посока на движението.
-
Скенер, имаш ли възможност да дадеш повече подробности, защо премащабиране ("мачкане") на пространство в зависимост от посоката на вектора на скоростта, при абсолютно време, което не е измерение (ако искаш, можеш да дефинираш времето като измерение, но също можеш и да не искаш), елиминира принципа на относителността?
-
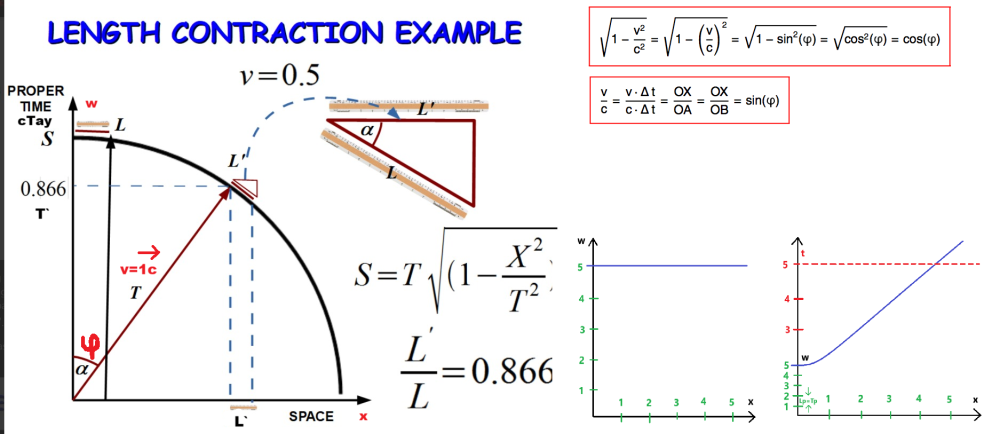
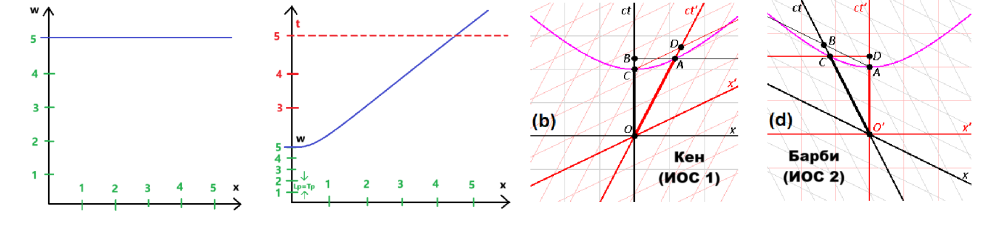
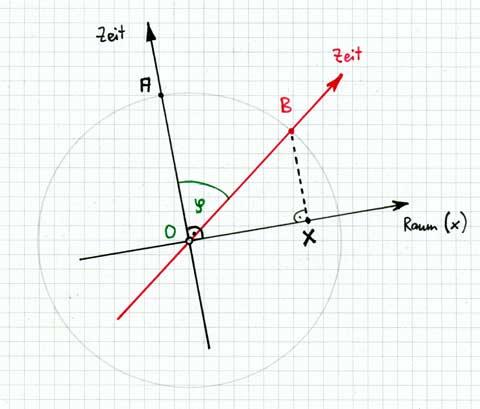
Ако не греша, щом времето не е абсолютно, а е относително - връзка с него има. Директният начин е да установиш Лоренцовите трансформации, да наложиш айнщайновите постулати отпреди Минковски и така ще имаш обичайно 3D-описание с време, което не е измерение. Това е аналог на оценяването на ефектите от зрението ти през 2D-"екран" - не приемаш наличието на трето пространствено измерение ("дълбочината" на "екрана"), а прилагаш разни наблюдателни постулати и закономерности, кога една форма на автомобил може или не може да те удари (примерно). Следващият вариант, геометричен, но не изцяло пространствен е - да приемеш времето за измерение, но не като пространствено измерение (3D+1D). Това прилича малко на патерица, но важното е, че работи и може да се предложи точна картина и по този, пространствено-времевия начин на Минковски. Това е аналогично на включването на трето измерение към зрителния 2D-"екран", но за разлика от широчината и височината, които си ги има отпреди това, "дълбочината" да е условна (2D+1D), защото - ти безспорно наблюдаваш картина само с широчина и височина и макар "дълбочината" да върши отлична работа, тя не е визуално осезаема по точно същия пълноценен начин и значи и не е същото нещо, може да е само условно трето измерение... Струва ми се прекалено застъпването, че пространствено-времевия подход е единствения възможен и нищо друго няма смисъл (че само 2D+1D визуален анализ има смисъл и допускането на пълноценна 3D-визуална реалност е невярно), но трябва да напредна много повече от сега в моята концепция, за да убедя в потенциала на 4D-пространствения подход всички "закърмени" с (положили много труд в овладяването на) пространствено-времевия подход на Минковски. Струваше ми се отлична възможност "Динамичната Вселена" и това е работеща дефиниция по принцип, но възможността и към нея да се приложи (на следващ етап) методиката с Блоковата Вселена не прави нещата толкова добре разграничени, колкото ми се искаше. Може да се върна обратно към "W-асиметрията" като много по-ясно илюстрираща същността на подхода ми, ще видим - ще помисля много внимателно над това... Векторът 1с само условно е на светлината, в действителност светлината си има собствено движение (нерядко то е по-малко от 1с - зависи от средата на разпространение) и при нея просто липсва времевата компонента (при подхода на Минковски за светлината излиза нулев пространствено-времеви интервал, понеже там има изваждане и като извадиш квадрата на времето ct от квадрата на посоката на движението х се получава НУЛА - резултат, въпреки факта, че светлинен лъч изминава доказуемо пространствено разстояние в 3D-обема хуz). При Пенроуз светлинният лъч е би-туисторна конфигурация, където два свързани туистора се "въртят" в противополжни посоки ("напред" и "назад" във времето, грубо казано), което води до липсата на времеви параметър от позицията на самата светлина (за светлината времето е спряло, ако тя можеше да го регистрира някак си). Векторът 1с при "Динамичната Вселена" неизбежно се завърта (единственото константно нещо при него е стойността 1с в четиримерно пространство), защото това е единствения начин да се дефинират скорости между 1с и 0с в 3D-пространството хуz. Представи си огромна река, с километрична широчина и много бързо течение (1с ), но много гладка и спокойна повърхност (заради огромния размер), без вълнички и други смущения. Всички неща в покой едно спрямо друго в 3D-областта хуz заедно ще се движат в едно и също направление по течението на реката - направлението по координатата w. Ако векторът 1с не можеше да се върти - нямаше да може да се напусне покоят между всички тези неща. За да почнат различните неща да се отдалечават едно от друго (да престанат да са в покой) в 3D-пространството хуz, техният вектор трябва да се отклони от общото дотогава направление по координатата w и да се завърти към някоя от другите координати х, у или z (или някакво междинно положение между тях). Само чрез това завъртане, когато скоростта 1с започне да разполага със съответни свои компоненти и по координата w, и в 3D-областта хуz, обектите могат да нарушат покоя си в 3D-областта xyz и да започнат да осъществяват там някакви регистрируеми движения един спрямо друг със съответната подсветлинна скорост (светлината пък се движи с 1с изцяло в областта xyz и няма компонент на движение по координата w). Според мен това е напълно равностойно на СТО описание на всичко, което наблюдаваме. Нещата, които се движат по координатата w (всички, които са в покой едно спрямо друго в 3D-областта хуz), се движат спрямо всички други неща, които не се движат изцяло по координатата w (не са в покой спрямо покоящите неща в 3D-областта хуz). Синусът и косинусът на ъгъла Фи - ъгъла на отместването на вектора на скоростта 1с от координатата w - дават същите стойности, които се получават и от разделянето на скоростите v/c (стойността Бета от СТО), както и стойността в знаменателя на Лоренц фактора (числителя е единица).
-
Така е, но има разлики в логиката когато времето се ползва и когато не се ползва като измерение. Може да се състави верен подход и по двата начина, но това ще са различни логики, които ще съвпадат само в крайните резултати, които дават относно измерванията (резултатите трябва да са верните, значи ще са еднакви и в двата случая). По същия начин има разлика и когато процеси с повече пространствени измерения се анализират през логики с по-малко измерения (едно е, когато анализираме особеностите на визуалните наблюдения през плосък 2D-екран и съвсем различно е, когато ги анализираме посредством 3D-простарнствена логика). Накрая - едно е, когато времето е просто параметър и чрез него се изгражда блоков подход (да, Динамичната Вселена също може да бъде представена и като статичен блок, заради наличието на времето и независимо, че в случая времето не е измерение) и по-различно (по-различна логика) е, когато времето не е само параметър, но и съвместява функциите на измерение. И в двата случая накрая можем да изградим състояние на Блокова Вселена, но ще има определени разлики, когато Блоковата Вселена идва от пространство-време с времето като НЕпространствено измерение и когато идва от геометрия с четири пространствени измерения. И по двата начина ще бъде вярно (и по двата начина накрая ще идват резултатите от Лоренцовите трансформации, които трансформации могат да се изведат чрез различни във всеки от двата случая процедури), но конкретиката във всеки от двата случая ще е различна.
-
Целият въпрос е дали координатата "Време (s)" е само параметър или е измерение. Когато е измерение, представянето е едно (пространствено-времевото със срезовете, движението се съчетава със статичната картина на времето като параметър и детайлите в 3D се представят по едни начини, например като наклони на срезовете и т.н.), а когато е само параметър, без да е измерение (концепцията на Динамичната Вселена) - тогава причината за релативистките ефекти е координата на четвърто пространствено измерение и тогава онова, което е срезове, техни наклони, кривини и т.н. при Блоковата Вселена тук е различни направления с еднакъв темп през четири пространствени измерения, техния ъгъл и неговите синуси, косинуси и т.н. Резултатът в 3D е абсолютно същия като при пространство-времето и Блоковата Вселена, само не се приписва статут на времето като измерение (джендър-практиките във физиката, където и измерение, и степен на свобода са най-различни по естеството си неща, както идеални точки без пространствени размери могат да имат "вътрешни" свойства и материални движения), а си има още едно, четвърто пространствено измерение.
-
Тука някъде ми се губи какво не пасва, защото на мен всичко си ми изглежда наред (когато се ограничаваме само до ефектите на СТО, без ОТО и квантовата механика)! Нищо не пречи две коли заедно да си вървят една до друга в някакво направление, с една и съща скорост, но двете да се считат една спрямо друга неподвижни - ти и топчето на билярдната маса, което е неподвижно спрямо теб, но заедно си се движите с 1с по направлението на координатата w, поради това протяжността по цялото измерение w е с планкова дължина, скоростта 1с се получава чрез умножаването на планковата дължина по планковото време, значи за теб и неподвижното спрямо теб топче (докато и двамата се движите с 1с по w) времевият параметър е планковото време (при умножаването по съответната стойност се стига и до едната секунда). Когато едната кола промени посоката си в различна от твоята, без да променя скоростта си 1с - тя вече няма да е неподвижна спрямо теб (спрямо твоята кола) в 3D-областта хуz, там вече ще се движи с някаква скорост под 1с, а с остатъка до 1с ще продължава да се движи по w. Обаче поради различните скорости на твоята и другата кола по твоето направление w, двамата вече няма да се считате неподвижни един друг, чуждият интервал в w ще се е удължил спрямо предишното му състояние (докато и двамата се движехте само по w), а пък дължината му по посока на движението ще ти изглежда съкратена. Всичко е напълно еквивалентно с Блоковата Вселена и напълно еднакво в 3D. Само пълната статичност и срезовете на Блоковата Вселена с нейното четиримерно пространство-време (3D+1D), са перманентно, непрекъснато движение с 1с и различни ъгли на вектора на това движение в 4D-пространство. Това е съвсем подобно на двуизмерния екран, през който виждаме третото пространствено измерение проективно, стереографски - дълга и права влакова линия в далечината ни изглежда да се събира в точка, макар реално да не е така. През 2D-анализ изглежда сякаш 3D-направлението се свива и даже го няма, но 3D-логиката показва различна картина. По точно същия начин 3D-пространттвените разсъждения дават една картина (релативистката реалност с Лоренцовите трансформации), пространствено-времевите 3D+1D разсъждения дават друга картина (геометрията на Минковски и Блоковата Вселена), а 4D-пространствените разсъждения дават трета картина, различна, но тясно взаимосвързана с останалите две (моето предложение за Динамичната Вселена). Някакъв вид хиперизмерно представяне на реалността е и Hopf fibration (това е и базата за туистърите на Пенроуз, чиято би-туисторна конфигурация представя светлинен лъч, но при Пенроуз е още по-сложно от просто Hopf fibration) и на практика по този начин се представя стереографско въртене на хиперсфера. И там има перманентно движение, не става дума просто за хиперизмерно евклидово пространство (наличието на стереографската проекция при представянето), но за съжаление все още не разбирам достатъчно добре нещата, за да ги дискутирам пълноценно.
-
Тогава как приемаш наличието на скорост 0 при работата с обичайната СТО? Всяко нещо, което не регистрираш да променя местоположението си спрямо теб го приемаш за неподвижно спрямо теб и с нулева скорост спрямо теб, независимо как се движат спрямо теб неговите съставни части (един автомобил като цяло може да не се движи спрямо теб, докато двигателя му продължава да работи, а в купето му деца да се бият с възглавници) и независимо как се движат спрямо теб разни други обекти. СТО съвсем спокойно си работи с нулеви скорости (покой), само не допуска скорости над 1с. Като нямаш абсолютен покой (и абсолютно движение) в 3D - как стигаш до статичната Блокова Вселена? Като разсъждаваш четиримерно (чрез три пространствени и едно времево измерение), нали? А щом може да се стигне до напълно статичното състояние на Блоковата Вселена при 3D+1D разсъждение, защо да не може да се стигне до равностойно еквивалентно разсъждение за перманентно динамично състояние на Динамична Вселена при пълноценно 4D-пространствено разсъждение?
-
Аз имам предвид на макрониво - там четвърто пространствено измерение (петизмерно пространство-време) не се регистрира. Засега микронивото не го засягам, макар да имам някои предварителни допускания - тоя вектор 1с на макрониво със съвсем конкретна посока в 4D-пространствен обем може да идва само по някакъв начин, свързан с гравитацията, включително и гравитацията на микрониво:
-
Въз основа на това, че алтернативната концепция с вечното движение на вселенската материя (алтернатива на статичността на Блоковата Вселена) е напълно еквивалентна и свързана с досегашните концепции относно СТО, не ги отрича по никакъв начин и ако четиримерното пространство-време работи безпроблемно както в СТО, така и в ОТО, а петмерното пространство-време не работи (на макрониво) по чак толкова безупречен начин - значи и четиримерната динамична пространствена концепция ще работи безпроблемно, а петизмерната динамична пространствена концепция няма да е толкова безпроблемна. Четиримерната динамична форма въобще не е произволна - точно както Евклидовата специална относително напълно се базира на пространствено-времевите конуси на Минковски и по никакъв начин не ги отрича, точно така аз допълвам този подход, като включвам към него четвърто пространствено измерение w, което е напълно свързано с диаграмата и конусите на Минковски и само ликвидира противоречието, отбелязвано от теб и Гравити, да се обяснява времето със скорост, която включва в себе си времето като компонент (при Евклидовата относителност се ползват координатите х, сТау и t и там, както и в старите ми представи, където напълно приравнявах времето t с четвъртото пространствено измерение w, тази критика е напълно валидна). Сега си има четвърто пространствено измерение w, има си съвсем отделен времеви параметър t, който не е измерение (нито условно, нито никакво), интервалът (отстоянието) на w си се удължава с отклоняването на скоростта 1с в четиримерното пространство от тази координата точно съгласно хиперболичното въртене при Минковски и въобще - всичко си съвпада напълно с Минковски, само не е четиримерно пространствено-времево, а е четиримерно изцяло пространствено (и така концепцията за статичната Блокова Вселена се изменя на напълно еквивалентната концепция за четиримерната пространствено Динамична Вселена, като и двете са верни, без да са напълно еднакви).
-
На първо време (преди да съм задълбал още повече, към гравитацията, където именно е заровено кучето) - струва ми се, че щом е възможно реалността на макрониво да се представи чрез четиримерно пространство-време, значи би могла да се представи (по алтернативен начин) и чрез четири пространствени измерения. Обаче след като не може да се представи успешно чрез пет-мерния пространствено-времеви подход на Калуца-Клайн - най-вероятно не би могла да бъде представена коректно и чрез пет пространствени измерения (пространствено-времевия подход на Калуца-Клайн ще е петмерна Блокова Вселена, а петмерен чисто пространствен подход би бил петмерна Динамична Вселена, където векторът 1с се изгражда от своите компоненти в пет пространствени измерения и изглежда, че реално не наблюдаваме подобна ситуация, поне не на макрониво).
-
Неподвижно според Минковски. Същността на Динамичната Вселена е тази, че неподвижност в действителност няма (точно както няма и движение при Блоковата Вселена). Как регистрираме някакви форми в пространството? Единствено и само чрез взаимодействия. На макрониво - основно електромагнитни взаимодействия (удари и отразена светлина). Има взаимодействие - има нещо с форма и размери, определени от взаимодействието (примерно - отразената светлина, която очите ни са уловили и на тази база мозъкът е създал съответната мисловна картина). На теб ти се струва неподвижен някакъв макрообект, но самата му регистрация е неразривно свързана с взаимодействия и движения.
-
Имай предвид, че при етернализма (Блоковата Вселена) ти нямаш достъп до 3D+1D пространство-времето, което е и блока. Ти работиш в хода на живота си само със срезове (времеви моменти в 3D) и нямаш пряк усет за целия статичен блок. А срезовете (времевите моменти) непрекъснато се сменят... По същия начин и при моята представа нямаш пълноценно, евклидово възприятие на 4D-ситуацията. Можеш да боравиш само с 3D и време. За да успееш да възприемеш напълно 4D-ситуацията в евклидовото ѝ естество, трябва да имаш способност за 5D-възприятие. Аналитично даден многомерен обект обикновено се анализира през условно евклидово пространство с по-висока размерност, което обаче не е реално, а само въображаемо, за целта на анализа. Нещо такова е и допълнителното времево измерение при пространство-времето на Минковски.
-
За да стане времето пето измерение, матрицата трябва да увеличи броя на компонентите си по диагонала от четири на пет, а аз имам предвид запазване на броя на компонентите на четири (времето не е измерение, както не е измерение и преди въвеждането на пространство-времето на Минковски, при обичайния айнщайнов подход с 3D-пространство и постулати). Ако матрицата стане пет-компонентна - тогава отиваме при Калуца-Клайн моделите, а тук не става дума за това. Нещата с тази концепция са много тясно свързани с туистърите на Пенроуз, в чиято основа стои Hopf-fibration (има и други детайли, но това е базата). Освен това и при Hopf-fibration има перманентно движение - този обект (както и туистърите на Пенроуз) постоянно осъществява стереографско въртене (и в двата случая се ползва стереографска проекция, при Пенроуз е проективно туистърно пространство, като при мен пък това стереографско естество се изразява чрез универсалното движение винаги с 1с през всичките четири пространствени измерения). Всичко това не означава, че не може да се стигне и до пет-измерна геометрия - гравитацията е свързана с неусетно (по инерция) движение с ускорение към масивен център (по геодезична линия, която в случая се явява най-късия път) и не съм сигурен дали това може да се представи само чрез четири измерения (движението с ускорение геометрично се изразява чрез движение по окръжност, а окръжността не може да се представи чрез по-малко от две измерения, макар сама по себе си тя да е едномерна) - това е новата ми цел за изясняване, с която ще е свързано продължението, когато имам някакъв напредък (увереност да изкажа нещо по-категорично).
-
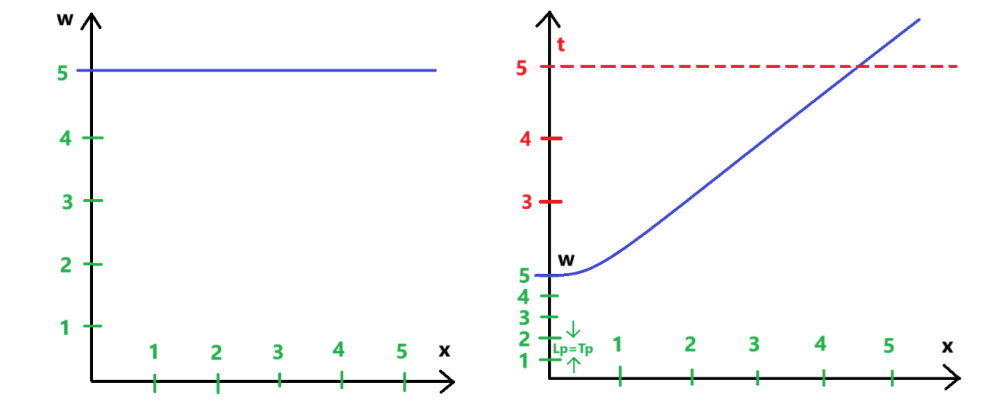
Като не местиш нещото по останалите три оси хуz. Ако имаш маса, да речем билярдна и топче, което се движи по масата, например към някоя от дупките - когато спреш това топче и то стои неподвижно до теб, който стоиш неподвижно до масата, топчето и ти се движите с 1с по оста w. Всички останали неща, които не са неподвижни спрямо теб и топчето, се движат с някаква скорост между 0с и 1с в обема на хуz, а остатъка до 1с е по w - тяхното движение по w е с по-ниска скорост, отстоянието, което те изминават по w е по-голямо от отстоянието по w, което изминавате ти и топчето и това се регистрира като удължен времеви интервал (при сравнение на часовниците тяхната секунда е била по-дълга от твоята и на топчето секунда). Времето не е измерението w, но е параметърът, чрез който можеш да си направиш извод за особеностите на 4D-пространствената геометрия, от която произтичат съответните физическите регистрации. Би могло да се каже, че анализ през пълноценна 4D-пространствена геометрия елиминира нуждата от употребата на "патерицата" пространство-време, където времето не е пространствено измерение за разлика от останалите три, но това е твърде силно казано. Просто говорим за още един алтернативен верен начин за представяне на релативистките особености, в допълнение на НЕпространствено-времевия 3D-подход, съчетан с айнщайновите постулати и на 3D+1D пространствено-времевия подход на Минковски - пълноценен 4D-пространствен подход, където времето не е измерение, както не е и при 3D-подхода с айнщайновите постулати в допълнение. Тези три алтернативни призми на анализ на физическата реалност (през 3D, през 3D+1D и през 4D) са напълно равностойни една с друга и всичките три дават верните резултати.
-
ДИНАМИЧНАТА ВСЕЛЕНА – ЕКВИВАЛЕНТНАТА АЛТЕРНАТИВА НА БЛОКОВАТА ВСЕЛЕНА Блоковата Вселена или още Етернализма е една от трите основни метафизични представи за времето, които са се наложили в най-голяма степен до момента – Етернализма (Блоковата Вселена), Презентизма и Нарастващата блокова Вселена. Докато според Презентизма съществува само настоящето (настоящето единствено се променя с времето, а миналото и бъдещето просто не съществуват) и според Нарастващата Блокова Вселена съществуват само настоящето и миналото (бъдещето не съществува), то според Етернализма и Блоковата Вселена всичко, свързано с времето – минало, настояще и бъдеще – съществува едновременно, в един статичен „блок“ на миналото, настоящето и бъдещето, без никакво движение, при което настоящето е само срез от този блок, а „ходът на времето“ е последователно редуване на множество такива срезове. Противоположната представа на етерналистката статичност може да се нарече интерпретация за Динамичната Вселена. Според тази представа вселенската материя се движи с абсолютен, универсален, винаги един и същ темп 1с (скоростта на светлината във вакуум) през сложна, нееднородна геометрия на Вселената с четири реални пространствени измерения. Смяната на посоката и на скоростта между 0с и 1с на наблюдаван обект от гледна точка на покой в 3D-пространството xyz или в 4D пространство-времето txyz може също да се обясни и като завъртане на вектора на универсалната, единствена скорост 1с в 4D-пространство wxyz. В последния случай липсата на скорости, различни от 1с, наличието само на един-единствен темп на материалните промени, практически обезсмисля говоренето за скорости и време, а само за геометрии на различни 4D-пространства, със съответните направления на 1с-векторите им, които пространства взаимодействат или не взаимодействат помежду си. Въпреки липсата на смисъл да се говори за различни скорости и време при подхода за Динамичната Вселена, време все пак има. За разлика от пространствено-времевия подход на Минковски обаче, тук времето не е измерение, а просто физически параметър, който съпътства вечното материално движение със споменатия винаги един и същ, абсолютен темп 1с в 4D-пространството и съответно времето като най-обикновен, различен от измерение параметър присъства и при анализи на определени части от Вселената и през три, през две и през едно пространствено измерение. Естествено, бидейки времето най-обичаен параметър, без проблем то е и относително (стойността му зависи от движението между различните физически обекти и не е инвариантна). За разлика от анализ през 3D-пространство с време, което не е четвърто условно, непространствено измерение, Динамичната Вселена е с 4D-пространствена геометрия. Всичко това означава, че при този алтернативен, еквивалентен на Блоковата Вселена подход, пространствено-времевия интервал S от подхода на Минковски тук има изражение в метри и така представлява обичаен пространствен интервал, но произтичащ от движение в реална четириизмерна геометрия. Лоренцовите трансформации много лесно могат да се получат от косинуса на ъгъла Фи, а параметъра v/c или още наричан Бета представлява синуса на ъгъла Фи. Макар и напълно равностоен на пространствено-времевия (Лоренцовите трансформации и всичко останало могат да се получат без проблем), подходът на Динамичната Вселена с четири пространствени измерения не е пространствено-времеви подход, каквито са подходът на Минковски, на Епщайн, на Евклидовата специална относителност и други подобни (всички те смесват пространствена координата с времева координата, което приравнява времето на условно измерение и прави всички тези подходи пространствено-времеви). Също така този подход не е и форма на Калуца-Клайн подходите, защото за разлика от тях матрицата на метричния му тензор се състои от само четири компонента (времето при Динамичната Вселена не е измерение и не присъства в четири-компонентната матрица като пети компонент, нито като някой от останалите четири пространствени компонента), докато матриците на Калуца-Клайн подходите са пет-компонентни. Следва продължение...
-
В такъв случай остава само да докажеш твърдението ти - демонстрирай ни скорост на движение на нещо поне с 2с. Знаеш, че автомобил може да се движи както с 1 км/ч, така и с 10 км/ч, и със 100 км/ч, и с 1000 км/ч (Thrust SSC - 1223.657 км/ч)... Ако СТО е невярна и не съществува ограничението до скоростта от светлината (едно от следствията на СТО) - без проблем можеш да намериш нещо, което се е ускорено поне до 2с (аз не искам 10с, 100с, 1000с, стига да ни покажеш и нищо, което да се движи само с 2с). Ето така, съвсем лесно, можеш да затвориш устите на всички релативисти - с доказателство, че не ни губиш времето просто с бля-бля!
-
Добре, де - кое точно е невярното? Защото е едно да кажа, че ти не разбираш нищо от физика, друго е да кажа, че не разбираш конкретно айнщайновите теории и квантовата механика и е трето да кажа, че не разбираш само СТО. Колкото по-обширно е моето отричане на твоите физически познания - толкова повече обяснения трябва да дам, защо точно смятам така, нали? Така е и с теб в този случай - конкретен детайл от ротация на Пенроуз-Теръл и/или свиването на Лоренц-Фицджералд ще избереш да обясниш защо не е верен, СТО като цяло ли или и СТО, и ОТО, където вече ще ти трябват къде-къде повече обяснения?
-
Кое не ти е убедително? Защото Гравити е дал доста детайлно обяснение и е добре да цитираш конкретни фрагменти, за да можеш след това да покажеш кои точно са неубедителните моменти. Така изглежда като някой да ти каже: "Ти не разбираш нищо от физика, затова аз ще ти покажа един номер с каране на карета от огнедишащи змейове..."
-
Разбира се! Ако езикът математика ти казва, че получаваш 300 лева аванс и 2000 лева заплата, но ти изхарчваш 1800 лева месечно и парите ти свършват - явно нещо в езика математика, нещо във формулата, която ползваш, не е наред (нютоновата механика, която, на всичкото отгоре, се е отказала от явно относителното галилеево пространство в полза на абсолютните пространство и време - първоначално Нютон е смятал да дефинира повече от известните само три закона, сред които повече е била и галилеевата относителност, но после се е ограничил само до трита си закона и с това е загубил възможността да сбърка само с абсолютното време). Обаче, ако езикът на математиката ти казва, че получаваш аванс от 300 лева и заплата от 1500 лева и месечно харчиш точно сбора от 1800 лева - значи тук математиката вече е точна и съвпада с реалността (СТО). Както езикът можеш да го ползваш и за верни и за неверни твърдения (примерно - като перманентните лъжи и измишлшзми на Тръмп), така и математиката можеш да я ползваш по верен (Айнщайн) и неверен (Нютон) начин. Нютоновата представа за абсолютни пространство и време се оборва още от Галилей преди него - галилеевия принцип за пространствената относителност (от което произхожда и галилеевото събиране на скорости). И Нютон е бил наясно с това!