Станислав Янков
Потребител-
Брой отговори
2763 -
Регистрация
-
Последен вход
-
Days Won
1
Content Type
Профили
Форуми
Библиотека
Articles
Блогове
ВСИЧКО ПУБЛИКУВАНО ОТ Станислав Янков
-
Причината е, че не съм в състояние да приема сериозно реалното съществуване на покой и възможност за материални промени без промени в пространството. Да, когато летя в самолет при безоблачно небе и виждам някъде далече долу реката Дунав като една извиваща се ивица неподвижност, аз не различавам никакво движение, но не мога да изключа, че всъщност реката непрекъснато се движи, тече и това се вижда съвсем ясно в близост до нея, чувства се, когато някой плува вътре в нея (дали движението се закрива заради далечината/мащаба или защото изображението е размазано заради ниска разделителна способност - няма значение, това са два различни начина на описание на едно и също нещо). Разбирам всички обяснения, не съм глупак, просто не мога да приема реалност на покоя, независимо от философските и всички останали съвсем не безсмислени аргументи с много дълга история, защото - зная за движението в пространството, което винаги се крие зад измамната привидност на покоя (неподвижността)!
-
Съгласно това, което съм учил някога в училище и което срещам във всички общодостъпни обяснения - перонът Е неподвижната ИОС, когато към него е приложена неподвижна координатна система с часовник и тогава избрана специална негова точка (като неподвижен спрямо перона наблюдател върху перона) се явява центъра на координатната система. Всички други неподвижни спрямо перона неща (къщи наблизо и далеч, самата земна повърхност, където е изграден перона и т.н.) са част от тази инерциална система (дори и неподвижна, системата си остава инерциална, защото според разглеждането нищо не ѝ въздейства и да се стреми да я извади от инерционното състояние на покой). Всичко останало, което се движи спрямо перона и неподвижния върху него наблюдател (или просто пейка на перона, стълб, врата - все едно какво, стига да е неподвижно спрямо перона) са една или повече различни инерциални системи, в зависимост от условието на задачата. В случая - влакът е отделна инерциална отправна система (има пълното право при други условия на задачата влакът да се разглежда като неподвижната система, а перонът като подвижната), защото се движи с постоянна скорост спрямо перона. Тук се игнорират разните въздействия върху влака на гравитация, въздушно съпротивление, триене и каквото и да било друго, интересува ни само инерциалното движение на влака спрямо перона или обратното (на перона спрямо влака) и затова става дума за инерциални отправни системи. Същото е и с два кораба в Космоса, които се отдалечават с някаква постоянна скорост един от друг (при едни условия на задачата единия кораб е инерциалната отправна система в покой, с прикрепена неподвижно към него идеална, абстрактна координатна система с часовник, при други условия това е другия кораб) и т.н. Въведение в отправни системи (видеоклип) | Кан Академия Започване на Нютонова диаграма за път и време (видеоклип) | Кан Академия Видях дискусията отпреди години между Скенер, Гравити и Дорис относно системите (координатни, отправни, инерциални, неинерциални...): В случая не става дума за никакви флуиди, газове в Космоса, нехомогенни магнитни, електростатични, електромагнитни, гравитационни и каквито и да било други подобни полета, става дума за най-баналните примери с два кораба, с влак и перон и т.н. - с две най-обикновени инерциални отправни системи, всяка от които има равното право тя да се счита за покоящата и които се движат в пространството с постоянна скорост една спрямо друга. Никога, откакто пиша тук, не съм разглеждал нещо различно от най-баналното и често срещаното, никакви случаи с неинерциални системи, флуиди, газове или каквито и да било нехомогенни обемни състояния. Всичко различно от простото инерциално движение с някаква постоянна скорост между две системи е ненужно отклоняване на дискусията от същността, излишни косми. Всички последващи разсъждения се базират на тази основа. Прегледах набързо философските аспекти около материята, материализма, даже отново прегледах метафизиката, онтологията, епистемологията (тези ги бях преглеждал веднъж преди време, покрай някои от коментарите на Кипен), аз уважавам философията и въобще не я считам за безсмислена, но в случая това също ми се струват отклонения от същността на дискусията, съвсем достатъчни са си физическите дефиниции на материя (всичко, което взаимодейства), покой/неподвижност (две или повече точки да не променят пространствените си отстояния с времето), механично движение (противоположното на покоя, с разграничаването на транслационните и ротационните движения). Добре е да се знаят допълнителни и още по-задълбочени неща, но в случая стигат и конкретните физически дефиниции. Моите разсъждения се базират на движението като основен, водещ елемент, а покоят е второстепенен, условен, илюзорен елемент. Не може покоят, неподвижността в пространството, да не може да се регистрира като реално съществуващ на всички равнища, но да се определя като равностоен на движението в пространството. Той може да е само условен и тогава онова, което се определя като резултат на пространствено-времева геометрия, може да бъде резултат единствено на реална четиримерна пространствена геометрия. Приемането на четвъртото условно времево измерение като реално четвърто пространствено измерение наистина е постулат, докато не се разкрие целия механизъм на проява на реалността от тоталното НИЩО. Постулирането на този етап се запазва, само се измества малко по-нататък, но тази стъпка се базира на невъзможността да се демонстрира реален покой в пространството, без да се „замъглят“ перманентните, непрекъснати движения в пространството чрез сетивно/мозъчните и инструментални ограничения при достатъчно голям мащаб. Реалният покой също има място, но дефинирането му би трябвало да се постига по някакъв различен от сегашния начин, свързан с тоталното НИЩО. Условността на покоя спрямо движението въобще не пречи да си се работи с покоя напълно нормално по утвърдения досега начин - статика, кинематика, динамика и всичко останало в тази връзка. Само става дума за акцент над движението в пространството спрямо покоя на някакво равнище на разсъжденията относно физическата реалност. Абстрактния, идеализиран преглед на реалността е като идеален „филм“, „плака“, „пласт“, през който се анализира реалността – реалността е такава, каквато е и ние ползваме идеализирания/абстрактен „филм“ за открояването и оценяването на разни нейни аспекти. Абстрактен, идеален, въображаем мисловен конструкт за максимално изчистен и фокусиран анализ на сетивната и инструментална „външна“ реалност. Това нещо освен в човешките представи, реално го няма никъде другаде (разните камъни, личинки, по-големи животни като сърни, лъвове, слонове и даже човекоподобните маймуни нямат подобен представен инструментариум за оценяване на сетивните постъпления към нервната и мозъчната им система, когато въобще разполагат с такава), това е просто една човешка измислица с полезни практични предназначения и не ми изглежда смислено подобни абстракции и идеализации да се ползват като основание за отричане на заключения, базирани на сетивността и обективността. Какво означава покой, неподвижност в пространството, когато на практика всичко се върти, свива, разширява, променя си формата, мести се – движи се в пространството, транслационно и/или ротационно, подобно на флуид или газ, когато не засягаме квантовите мащаби и цялото това движение в пространството, цялото това постоянно трептене е перманентно, тотално, навсякъде? Прави се опит да се отрече ролята на материалното движение в пространството относно естеството на времето, като се използват аспекти (часовниковите) на този идеализиран, абстрактен „филм“ срещу реално регистрируемия факт, че реален покой (неподвижност) не съществува, ами това е условно състояние, което се дължи на сетивно/умствените и/или на инструменталните ограничения да се отчитат някои от материалните движения в пространството и поради това покоят не е равнопоставен на движението в пространството. Покоят, неподвижността в пространството, е точно същата абстракция и идеализация, както идеалните часовник и линийка, употребявани в СТО (и не само там). Идеално-точният часовник е светлинният часовник от известните мисловни експерименти. Дори и тази съвършена конструкция, която е невъзможна за практическа реализация, ползва пространство за своето условно функциониране. Без употребата на материално движение в пространството реализацията на часовников темп, в най-широкия смисъл, е невъзможна. Също и уж равностойното на трите пространствени измерения четвърто времево измерение реално не е точно равностойно и едносъщно на тях, защото на него се отказва възможността да е пространствено като тях. С времето ще прегледам отново всички контра-аргументи срещу изложените мои представи, аз извличам значителни ползи от всичко това, макар редица квалификации по мой адрес да са излишни (аз не си позволявам подобни в момента) и макар някои да считат, че няма никакъв ефект и нищо не се променя. Това обаче няма да е скоро, че изникнаха някакви тъпи проблеми в работата, които най-вероятно ще се отразят и на мен, а все пак - работата е най-водещ приоритет...
-
Това, че СТО се базира на постулати, вместо на обяснения, веднага трябваше да „светва лампичката“, че тука има нещо недовършено и да води поне до някаква идея смирение и на най-големите разбирачи на относителностите (и с това аз не отричам, че някои разбирате наистина много и със сигурност разбирате повече от мен). Всичко онова, което при 3D-пространство трябва да ползва постулати, безпроблемно (макар и не лесно) получава обяснения с 4D-пространство. За придвижване между точките А и Б е необходимо протичането на някакво време заради изминаването на някакво пространствено отстояние и това не може да се замаже с определянето на часовниците като идеализации и абстракции. Има по-бързо изминаване на едно и също пространствено отстояние за по-кратко време или по-бавно изминаване на същото пространствено отстояние за по-дълго време, но не съществува мигновено телепортиране. Не съществува и реален покой, никой от вас не може да ми даде пример за реален покой (за липса на промяна на местоположението в пространството дори и при по-внимателно вглеждане, не само при повърхностната привидност). Всичко, което при 3D-пространство се обяснява "с изменението на вътрешните характеристики на състоянието на материалните обекти във времето, т.е. в процеси, формирани в поредица от събития" или както аз го бях написал, като възможност да се случват неща без движение в пространството, „свойства на материята да се променя без изменение на местоположението в пространството“, може да се обясни и като пространствено движение в 4D-пространство и щом на вас ви харесва да отричате това – ваша работа! Време е да се разделим за по-малко или повече време, защо нещо започнах да се натоварвам, вместо да дискутирам с удоволствие, а това със сигурност е контрапродуктивно!
-
Тоест - аз съм длъжен да знам неща, които ги няма в учебниците (аз цитирам онова, което е общодостъпно и масово, включително част от масовото образование) и които се постигат след дълго и упорито усвояване с разбиране на купища тънкости и затова тука трябва да преминавам през сериозен изпит, за да имам право да комуникирам с вас, вместо по-знаещите от мен просто да ме опровергавате, само със съответните аргументи, без да се занимавате с психиката и личността ми, сякаш съм нещо виновен, че не знам колкото вас?! Скенер е прав - така няма да стане! Просто ще си направите това място бутиково - за кръг от няколко души, които винаги си се разбирате и сте си съгласни един с друг, в което, разбира се, няма нищо лошо!
-
Въпросите на Гравити: "Въпросът не е в това какво е инерциална отправна система, а какво е отправна система. Защото така както пишеш изглежда, че не ти е ясно." "Не, нямам това предвид, не коя е избрана за неподвижна, а какво е отправна система." Изглежда ли ти Гравити да ме пита за неинерциални системи и кога въобще е ставало дума в разговорите с мен за такива, че да трябва да бъда питан за това?!!! Затова казвам, че ми приписвате да твърдя неща, които никъде не съм твърдял и след това се борите с тях, заедно с всички съпътстващи "екстри" по мой адрес! Ето какво още казва Гравити: "Въпросът е каква е дефиницията на отправна система? Погледни линка, който се дал! Защото отправната система не е наблюдател нито влак или ракета. Всяко от тези неща се намира във всяка отправна система." От линка, който съм дал: "Отправна система е понятие от физиката за обозначаване на гледната точка на наблюдателя. То е от основно значение в теорията на относителността, където не съществува абсолютно движение и всяко движение е относително спрямо други тела. Тялото, спрямо което се определя положението и движението на другите тела, се нарича отправно тяло. То заедно с неподвижно свързани към него координатна система и часовник, чрез които се определя положението на другите тела спрямо отправното тяло в различните моменти от време, образуват отправната система." Къде тука има каквото и да било за неинерциални системи, че Гравити да има предвид това?!!! Нещо въобще, ама ВЪОБЩЕ не се разбираме кой-какво има предвид!!!
-
Всяка инерциална система може да се определи като отправна - въпрос на решение коя ще счетем за неподвижната и тогава другата ще е движещата се с някаква скорост. Както можем да определим едната за неподвижна и другата за подвижна, така можем да определим и другата за неподвижна, а едната за подвижна (когато има движение между тях, разбира се) - всяка може да стане наблюдателя, само да пожелаем така да е в задачата. Няма пречка ВСЯКА система да определим като от отправна/неподвижна, затова са равноправни или греша нещо?! Няма инерциална система, която да не можем да определим като отправна/неподвижна/наблюдател - навсякъде се базирам на това и не мисля, че нещо греша!
-
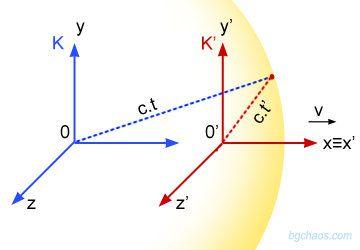
"Имаме две инерциални системи K и K', като втората се движи спрямо първата с постоянна скорост v ." Двете инерциални системи са наблюдателя (избраната за неподвижна) и наблюдавания обект (подвижната система, която се движи с някаква скорост и ролите тук могат да се заменят, когато искаме да разгледаме ситуацията от позицията другата инерциална система). Това може да са и наблюдател и влак, и два влака, и два кораба - две инерциални системи... Какво става тук?!!!
-
Въобще не говорим за неинерциални системи (най-често под това се имат предвид случаите с гравитация). Неподвижността не променя нещото относно инерциалността на системата: "Инерциална отправна система – отправна система, в която е валиден инерционният закон: всяко тяло, на което не действат външни сили, запазва положението си на покой или равномерно праволинейно движение."
-
Под отправна система аз разбирам онази инерциална система, която се счита за неподвижна (в покой) в съответната задача. Всяка инерциална система счита себе си за неподвижна и останалите за подвижни (ако някоя друга система е неподвижна спрямо така наречения наблюдател, бидейки той базовата неподвижна система - такива две системи могат да се считат за една и съща отправна система, докато не настъпи някаква промяна в това състояние и мисля, че Скенер искаше да каже нещо такова с последния си коментар).
-
Аз го знам така: "Инерциална отправна система – отправна система, в която е валиден инерционният закон: всяко тяло, на което не действат външни сили, запазва положението си на покой или равномерно праволинейно движение. Всяка отправна система, която се движи относно дадена инерционна система равномерно и праволинейно, също е инерционна. Съгласно принципа на относителността, всички ИОС са равноправни и в тях действат едни и същи физични закони." Отправна система – Уикипедия "9. Отправна инерциална система - отправна система, в която действа Законът за инерцията, който гласи: "Материална точка, върху която не действат никакви сили или действащите сили взаимно се уравновесяват, която се намира в състояние на покой или равномерно праволинейно движение". Всяка отправна система, движеща се спрямо друга инерциална система равномерно и праволинейно е също инерциална система." Специалната теория на относителността | Физика
-
При влак и неподвижен наблюдател на перон - инерциалните системи са влака и наблюдателя/перона (когато наблюдателя на перона не се движи спрямо перона). При два влака - инерциалните системи са единия и другия влак (същото е и при две ракети). При пирони - инерциалните системи са пироните и нещо друго или два отделни пирона, две купчини от пирони, пирон и купчина пирони... Това имах предвид. Това не е важно, принципно разбирам какво искаше да кажеш.
-
Мога да го напиша и различно, съвсем директно. Защо можем да разкараме часовниците, въобще да ги няма, а не можем да разкараме и влаковете (ракетите и прочее) - тях също въобще да ги няма? Нали както се ползват абстрактни, идеализирани часовници, така се ползват и абстрактни, идеализирани линийки (както за по-голяма точност са нужни по-сложни часовникови устройства, така и за по-голяма точност са нужни по-сложни "линийки" - лазерни устройства и прочее)? Не мислиш ли, че има нещо ненаред в това положение?! Или ако може въобще и без часовници, и без влакове (ракети и прочее...) - тогава каква е въобще връзката на подобно разсъждение с реалността (със сетивните регистрации)?! При условие, че имам предвид материалното движение В ПРОСТРАНСТВОТО по принцип, изчистено от всякаква конкретика, като идеализация, като абстракция - защо това да се приравнява с изчисляване на поведение на листа и прочее излишни усложнения? Аз не казвам "часовник с атомно, електронно, махално" или все едно какво друго конкретизирано устройство, аз казвам - някакъв (идеален, абстрактен) часовник, с някакво (идеално, абстрактно) устройство, свързано с някакво (идеално, абстрактно) материално движение в пространството. Такъв часовник не може да влияе на резултата с несъвършенствата си, защото си остава съвършено-точен като просто часовника, но включва факта, че по никакъв начин не можеш да формираш часовников темп, без да ползваш НЯКАКВО (все едно какво точно, без никаква конкретика) материално движение в пространството. Покоят, принципно, не е сложно какво е - неподвижност, липса на промяна в пространственото отстояние между две точки с времето. И тук веднага идва въпросът - съществува ли такава абсолютна неподвижност в реалността? Привидност за такава безспорно съществува - всичко, което ни се струва неподвижно на макрониво. Представи си, че зла инквизиционна служба на диктаторски режим иска да изтръгне от теб важна информация срещу децата ти и те е подложила на страшно мъчение - обездвижила те е в напълно тъмно помещение, в което не си в състояние да регистрираш абсолютно никакво движение (абстрахираме се от детайла, че без мозък въобще няма как да разсъждаваш и регистрираш и това е най-чистата ситуация без време). Както знаеш - тогава ще загубиш всякаква представа за ход на времето. Знаеш случаите с изолации без часовник, например в пещери, при което при по-дълъг период хората губят точна оценка колко време е изминало, независимо какви усилия полагат това да не стане (при убийство, при спиране работата на мозъка им, въобще ще изгубят възможност за регистрация на най-абстроктната последователност ПРЕДИ-СЕГА-ПОСЛЕ). За каква промяна на материята бихме могли да говорим, когато АБСОЛЮТНО ВСИЧКО В ПРОСТРАНСТВОТО Е В ПОКОЙ (неподвижно, произволни избрани точки не променят пространствените отстояния помежду си)?!!! Кипен да не си въобразява, че не чета коментарите му - ще ги прочета през уикенда и най-внимателно и не веднъж.
-
Наясно съм какво си написал, подчертаваш "промяна на материята" като възможност да се случват неща без движение в пространството и затова се казва пространство-време. Обаче не можеш да ми покажеш ДОРИ ЕДИН СЛУЧАЙ на реален покой в пространството на макрониво (винаги, когато понамалиш мащаба, при това не чак до дълбоките квантови равнища, неща като коли и други макрообекти, които изглеждат неподвижни, непрекъснато трептят и се движат в пространството - реален покой няма, особено от едни нива надолу). Чета ти коментарите, независимо как ги разбирам и независимо че не е веднага, а най-често към края на седмицата. Чета коментарите и на Скенер, Гравити, Шпага, вече почнах да чета и тези на Младенов, защото от известно време започна да цитира полезни неща. Чета ви коментарите многократно, включително и някои много стари (отпреди години). Лек ден!
-
Аз се опитвам да намекна, че "часовник" не е някакво специално устройство, а часовник е самото движение, промяна на материята В ПРОСТРАНСТВОТО, като идеализирана същност, без никакви подробности. При тотален покой на абсолютно всичко и при движение на абсолютно всичко само с една скорост не може да се формира никакъв часовников темп, нито дори усет за най-обща последователност ПРЕДИ-СЕГА-ПОСЛЕ, без никакви други уточнения и конкретизации. И питам следното: При условие, че и "линийките за измерване" и "часовниците във физиката" са еднакво идеални и абстрактни (иначе сметките с Лоренцовите трансформации се обезсмисляли и в това има логика) - защо да имаме право да говорим за вътрешното пространствено отстояние при влакове, ракети и прочее, в зависимост от примера (там се задействат фенерчета, движат се лъчи от тези фенерчета и т.н.), но да нямаме право да говорим за пространство при движението на частите на часовник (без такова движение на часовникови части в пространството въобще не може да се изгради часовник)?! Няма никакъв проблем идеалният/абстрактен часовник да има идеално/абстрактно устройство и пак да си дава съвършените отчитания, необходими на СТО! Няма никакви влияния от страна на подобен часовник! Защо можем да говорим за вътрешно пространство на вагони, а не можем да говорим за пространство, в което да се движат чарковете на съвършената конструкция на идеален, абстрактен часовник, при абстрактни/идеални както часовникови темпове, така и мерителни линийки?! Стилът ви на комуникация на някои е такъв, че вече съжалявам защо се обадих отново! Просто не можете да се абстрахирате от моята личност, от правенето на психологически анализи и от постоянното натякване, колко ограничени били познанията ми (никъде не съм парадирал с противното) и да се фокусирате над задаваните от мен въпроси! Постоянно отговаряте на неща, каквито не питам! И, честно казано, не питам чак такива глупости! Огромно мнозинство хора не ги разбират всички тези тънкости, не съм само аз!
-
Писането по нощвите си е казало думата! Корекция: Или има неравностойно третиране между пространството във връзка с влаковете и пространството във връзка с часовниците, или освен реално, абсолютно материално движение в пространството, има някаква друга, алтернативна област на случване на материални движения във връзка с инерциалните системи, разглеждани помежду им и всичко там е само една паралелна на реалното пространство, тотална, идеална абстракция (идеални абстракции са и часовниците, и линийките или всякакви други практически способи за мерене). Нещо, отделно от движението в пространството в реалността.
-
Линийката не може да има реално пространствено отстояние, приемането на реално пространствено отстояние на линийка обезсмисля идеално-точната пространствена протяжност, която се ползва в Лоренцовите трансформации, часовникът не може да има материален темп в реалното пространствено отстояние, приемането на материален темп в реалното пространство обезсмисля идеално-точния часовников темп, който се ползва в Лоренцовите трансформации… Така излиза, че може въобще без реалното пространство и че то не играе никаква роля като реален феномен, нито при часовниковите темпове, нито при пространствените отстояния (всичките тези са единствено и само съвършени идеализации и абстракции) - абстракциите са взели връх над реалните разсъждения!!!
-
Налага се да се допитам до теб набързо, после пак се изключвам! Прав ли съм да смятам, че голямата колизия е в това - дали покоят е реален или е условен? Ако покоят е реален, значи може да има и движение на материята без такова в пространството и четвъртата времева координата е условна, всичко протича в пространство-време с едни и същи характеристики за всички инерциални системи, а ако покоят е условен – тогава движението на материята може да е само в рамките на пространството и четвъртата времева координата е реална пространствена по някакъв начин, а пространствените реални четиримерни характеристики са индивидуални за всяка отделна ИОС (когато различните ИОС не са в покой една спрямо друга). При тотален покой, когато абсолютно нищо не мърда в пространството по никакъв начин, не може да се отчете никакво време, никаква последователност ПРЕДИ-СЕГА-ПОСЛЕ на материалното движение в пространството дори в най-общ план. При тотално движение – може, стига да могат да се изявяват по някакъв начин различни скорости на движение, даже и в ограничения диапазон между 0с и 1с. Мисля, че разбрах точно забележката ти (първоначално фокусът ми беше над други неща)! Да, ама при влаковете никой не твърди, че не могат да имат никакви пространствени движения вътре в тях (от сорта на светването с фенерче и лъча светлина от него, който се разпространява в пространството на влака), че цифрите на скоростта на движение между влаковете и на дължината им по посока на движение, които се ползват в Лоренцовите трансформации, идват от идеализации и абстракции и че заради това нямаме право да говорим за вътрешни пространствени процеси във влаковете, те не участвали по никакъв начин и затова не ни интересували, че реалните влакове нямат значение и нещо повече – с обсъждането им ще увредим чистотата на Лоренцовите изчисления и чак ще ги обезсмислим! Че движенията вътре в тях в действителното пространство нямат значение, защото са излишен шум, който трябва да се ореже в полза на абстракциите, иначе изчисленията (Лоренцовите ефекти) са направо невъзможни! Включването в анализа на вътрешните движения на влаковете било тяхна намеса и влияние в схемата на СТО-логиката, а не те да са повлияни от пространствена геометрия, еквивалентно на пространствено-времева геометрия. А с часовниците всичко изброено се прави!!! Или има неравностойно третиране между пространството във връзка с влаковете и пространството във връзка с часовниците, или освен реално абсолютно пространство на покоя, има някаква друга, алтернативна област на случване на материални движения във връзка с инерциалните системи, разглеждани помежду им и всичко там е само една паралелна на реалното пространство, тотална, идеална абстракция (идеални абстракции са и часовниците, и линийките или всякакви други практически способи за мерене). Нещо, отделно от пространството в покой в реалността. Че не съществува никакъв начин всичко това да се представи и по алтернативен и напълно равностоен начин, чрез четири реални пространствени измерения!
-
Точно тук е несъгласието ми. Че не съществува възможност да няма часовник. Часовник не е нещо специално с циферблат. Часовник е самото движение на материята в пространството - като най-обща концерция, идеализирано, без подробности. Практически това би било изключително неточно часовниково разграничение (оня пример, който ти дадох, с полета на птицата и ПОСЛЕ, без конкретизация на това после, но ПОСЛЕ, да се спънеш). Най-общата и неконкретизирана последователност ПРЕДИ-СЕГА-ПОСЛЕ, която няма как да се реализира без движение на материя в пространство, РЕАЛНИ! Покоят го има, но само условно, като сетивни и мозъчни ограничения. Не е достатъчно само да заявиш "времето е чиста абстракция, свойство на материята да се променя с движение, но не в пространството, даже можем и без никакъв часовник, защото всичко това е абстракции" и с това да си измиеш ръцете от връзката на общото понятие "часовник" с материално движение в пространството (идеализиран часовник, но с устройство, някакво, неопределено конкретно и някакво, неопределено конкретно, движение на неговите идеални части в пространството). Така се къса връзката с реалността - пак абстракция, но по-непосредствена, директно свързана със сетивността и усета ни, на която би трябвало да се базира всичко, включително и най-отвлечените останали абстракции. И ако за математическите операции на СТО може и да стига, то за определяне на реалната същност на времето, като практически феномен, на мен ми изглежда недостатъчно (абстракция, която достига прекалено далеч). От друга страна, Скенер е прецизен човек и не пише случайни неща, Гравити също, Кипен също, ти също. Затова ще си дам почивката (една, две, три седмици...) и ще прегледам по-внимателно всичко това и - ще видим... И вече е време реално да го направя, че прекалено много взех да отлагам финала на коментирането ми!
-
Дори и идеални, формите от Платоновия математически свят на Пенроуз (тетраедри, кълба, кубове и прочее) все пак си остават съответните форми, само са идеални. А какъв е смисъла от идеален часовник без механизъм, пък бил и този механизъм идеален и неопределен?! Какво общо има подобно безструктурно и безсъдържателно нещо с часовниците, освен названието?! Дори и идеален, един часовник все пак би трябвало да прилича в общи линии на часовник! Сега разсъжденията са такива, сякаш идеалните часовници нямат никакво устройство. Това е нереално! Идеалните часовници също трябва да имат устройство, което функционира чрез движения в пространството, независимо че устройството им също е идеално, а поради това и неопределено в конкретика. Просто имат някакво неопределимо идеално устройство, което се движи по някакви начини в пространството и отчита съвършено-точни интервали време. Кой е виждал часовник без НЯКАКВО устройство, каквото и да е то?! Часовникови устройства всякакви, но все някакво има. Ако няма някакво движение в пространството на часовниковия механизъм (частите, които изграждат часовника, а не самия часовник), ако всичко във връзка с него е неподвижно пространствено – то не може да отчете никакво време. Просто, абстракцията трябва да отчита, че идеалния часовник има и някакво идеално устройство, което извършва някакви движения в пространството и отчита идеално-точни интервали от време. Идеализацията/абстракцията на часовниците е необходима, за да са те идеално точни, а не за да се ползва това като оправдание за отричането на неизбежното наличие на реално, материално часовниково (на частите на неподвижния като цяло часовник) движение с темп в пространството. Как ти ще установиш, че има ефект „забавяне на време“, ако няма преди това някакво движение в пространството като представление за такова "време", дори и около неподвижен втори обект (тогава и двамата сте неподвижни един спрямо друг и това движение и за двамата е часовниково движение, два часовника с еднакъв времеви темп), което да се „забави“, когато този втори обект се задвижи с някаква скорост спрямо теб?! Как се забавя неподвижността?! Не ти ли се струва именно това абсурдното и безсмисленото?! Какъв е въобще смисъла да се води подобен спор?!!! Напук ли?!!!