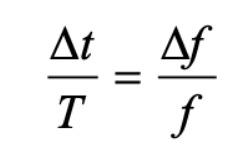Станислав Янков
Потребител-
Брой отговори
2763 -
Регистрация
-
Последен вход
-
Days Won
1
Content Type
Профили
Форуми
Библиотека
Articles
Блогове
ВСИЧКО ПУБЛИКУВАНО ОТ Станислав Янков
-
Знам, че те е страх! Усещаш, как накрая сам ще потвърдиш онова, от което всячески бягаш, като ощипана мома, затова и подхождам с това разбиране към теб... Имахме противоречие за двете скорости (ти още си под въздействието на оня материал на тримата) и проверявам, дали вече разрешихме това противоречие?
-
Ако ми отговориш - може и най-накрая да разбереш! Вече съгласен ли си, че имаме две различни скорости, когато регистрираме примерно скоростта на една кола спрямо нас - скоростта на колата и еталонната скорост на часовника, която очевидно е различна от тази на колата? Чрез сравняването на изминавания от колата път спрямо скоростта на часовниковите циклични промени определяме скоростта на колата. Скоростта на часовника не е същата като тази на колата, той си се движи със своя собствена скорост - имаме две скорости при регистрирането на скоростта на колата.
-
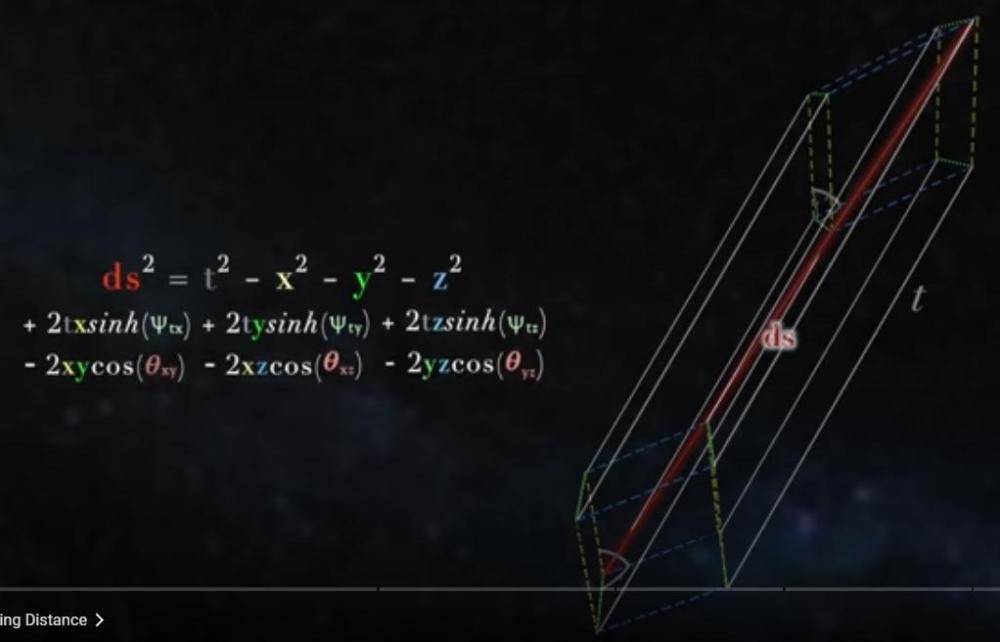
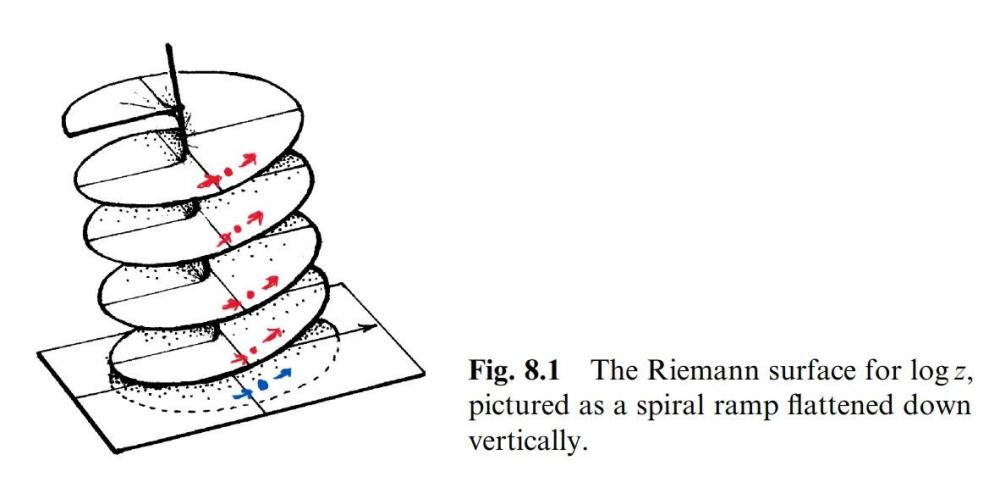
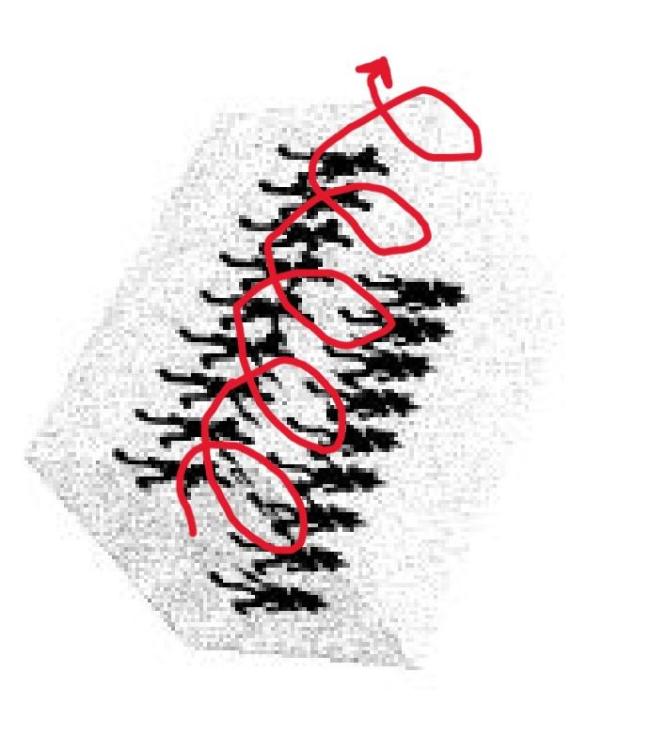
Понеже няма никакъв смисъл да си губим времето пълни глупости - да опитам нещо малко по различно... Евклидовата геометрия е приложима към обичайните три пространствени измерения, ако игнорираме разглеждането на времето. Това е обичайната трилъчева декартова координатна система, при която трита лъча излизат от общ център и са разположени всеки под ъгъл 90 градуса спрямо всички останали. Когато включим времето като четвърто измерение и ограничението до скоростта на светлината - геометрията вече става четиримерна неевклидова (в случая с диаграмите на Минковски - хиперболична). Ако съотношенията между времевото и пространствените измерения бяха обичайни евклидови, с линейни пропорции помежду им - щяхме да имаме обичайна декартова координатна система, но с допълнителен прав лъч и за четвъртото измерение, който също излиза от общия център на останалите и който също е разположен под ъгъл от 90 градуса спрямо всички останали лъчи на подобна координатна система. Хиперболичното неевклидово естество на връзката между времето и пространството означава не само, че тази връзка не е линейна (не е с линейна зависимост между времето и пространството), но също така означава и че геометрично тя не може да се представи само чрез прави, линейни координати (от тук идва и нелинейното, хиперболично естество на пропорциите между пространството и времето). Ако искаме да представим времето и пространството като четири неевклидови измерения, но по по-интуитивен и лесен за разбиране начин, може би най-удачни изглеждат следващите два еквивалентни геометрични начина: И в двата случая игнорираме едно от трите обичайни пространствени измерения, за да представим на негово място четвъртото измерение е така да облекчим иначе твърде сложното и неестествено представяме. На първото изображение четвъртото времево измерение е представено като права ос (координата), около която се вие спираловидно (с всички произтичащи от това деформации) промяната с времето на триизмерното пространство на Вселената (както вече беше споменато - на изображението едното от трите обичайни пространствени измерения е игнорирано и са представени само две). Ако искаме да представим същото нещо по много по-близък до нашето ежедневие начин, но който да е напълно еквивалентен на първия - ще трябва да "изправим" трите пространствени измерения, които при прав лъч на четвъртото измерение се вият около него като спирала, до обичайната евклидова триизмерна декартова координатна система, но тогава пък координатата на четвъртото измерение ще изгуби своя прав характер и ще придобие спиралоподобна кривина, с всички произтичащи от това деформации на връзката между нея и трите обичайни, вече изправени евклидово измерения (второто изображение, с триизмерни отрязъци пространство през планкови интервали време. Именно тази разлика на проявите на материята между трите пространствени и четвъртото времево измерение води до хиперболичното естество на връзката между пространството и времето, защото както и да се деформира/прегъва/увива връзката между трите пространствени и четвъртото времево измерение - тази връзка не може да се скъса и винаги ще се проявява пред нашите човешки възприятия и разбирания като пространство-време.
-
Демонстрирай ни, как йоносферата ти влияе? Започваш да пишеш още повече глупости или? Или поне някой научен труд, как по-точно йоносферата променя работата на най-точните в света атомни часовници, които са най-точни, точно защото не се влияят от нищо... Патологията при теб ще се окаже доста тежка, пич! А беше достатъчно само да прочетеш Уикито за атомните часовници, за да разбереш, че НЕ СЕ ВЛИЯЯТ от такива неща! Обаче - Чукча писаль, Чукча не читатель... Ние бистрим има ли механизъм/механика/взаимодействие/разход на енергия или няма и причината да няма разход на енергия/взаимодействие/механизъм при праволинейно равномерно движение с произволни скорости до С по световна линия, както при ускорение по геодезична линия, в основата си е една и съща - онова, което Скенер и Гравити се мъчат да ви накарат двамата с Младенов да прочете и понаучите, но както вече стана ясно - Чукча писатель, Чукча не читатель... Ако не можех да мисля с главата (както ти очевидно не можеш) - задължително щях да опитвам да ползвам часовник, който не може да се ползва за решаването на поставената задача и после щях да плача тука, че няма решение. След като си падаш по малоумието - предлагам ти да скочиш от най-високата сграда в София (оная, скандалната на Артекс), за да провериш, дали пясъчен часовник ще работи нормално, докато си летите надолу, както когато е на масата в кухнята (ето ти най-смислената употреба на пясъчния часовник, щом ти умееш да ползваш само него)... С егати и отчаяните глупаци бил пълен света!!!
-
Да, чрез ОТО. Това няма нищо общо с твойте пълни измишлизми, дето отрекоха цялата квантова механика, а ОТО - ти и нея отричаш, макар да е обяснението! Съществува ли някакъв дял от физиката, който ти да признаваш като приложим към твоя алтернативен свят или нищо от физиката не се прилага при теб? После отиди да си изпиеш хапчетата...
-
Може да се дължи и на извънземните, и на полета на щъркелите, и на всякакви други неща, но статията съвсем ясно ти казва, че се дължи на СТО и ОТО и без тях не се получава системата и това е доказано от практиката. И как всички тези неща влияят на функционирането на самия атом, което се ползва в атомните часовници (използва се в тези часовници вътрешното функциониране на атома и атомните часовници са най-точните, точно понеже всички тези неща НЕ ВЛИЯЯТ на вътрешното функциониране на атома - прочети поне базовите неща от квантовата механика)? Хора, пригответе се - ще ни разясняват чисто нова физика, която няма общо с учебниците отгоре-додолу!!! Обясни ми тогава, физико, къде е ускорението при РАВНОМЕРНО праволинейно движение - единственото инерциално (дори движението по окръжност е с ускорение и не е инерциално)? То и аз съм лаик, ама някои са направо цирк, който клони към пълна идиотия!!!
-
Как точно часовника си взаимодейства с гравитацията на Земята, по какъв механизъм? Гравитацията не въздейства осезаемо на вътрешното функциониране на атомите (ако все пак има някакво въздействие - то е толкова слабо, че все още не е открито дори и теоретично) и даже и гравитоните все още не са потвърдени (но дори и да бяха - въпросите пак стават повече от отговорите, предвид тяхното виртуално естество при взаимодействие).
-
А! Тука вече успя да ме изненадаш! Очаквах да не се съгласиш, защото според пред-релативистките (така наречените "нютонови") представи не само времето, но и пространството ("празното") е отделен от материалните взаимодействия феномен и по твоята предишна логика, "празното" пространство трябва да е "нищо" и "нереално" по същия начин, по който е "нищо" и "нереално" и времето. Чак след основаването на СТО и ОТО (изчислимото обвързване между пространството, времето и скоростта на движение) започват научните разработки за Големия взрив и налагането на научните представи, че и времето, и пространството са продукт на особеностите на материалните движения/промени (особеностите, аспектите на проявите на материята). Веднага щях да те попитам КАК ТОЧНО става това, ако беше написал, че пак някакъв механизъм на взаимодействия между обектите в пространството е отговорен и вече щеше да трябва да отговаряш ти, защото според мен за това е отговорна геометрията на пространство-времето (в тази дискусия се ограничаваме само до пространството, без да се занимаваме с времето, а само като три пространствени измерения, без участието на времето, пространството е триизмерно евклидово) и различните обекти просто следват неговата геометрия. Добре! Значи така много по-лесно от очакваното ще се разберем за следващото! Съгласен ли си, че когато говорим за движение само по едно-единствено направление през трите пространствени измерения, ние ВИНАГИ говорим за движение с две скорости, които се съчетават една с друга - скоростта на преместване на наблюдавания обект спрямо еталонна скорост на промяна на часовниковите цикли (часовниковото тик-так-ане)? Направление на движение през пространството не може да става без сравняването на тези две скорости, защото не съществува движение, което да протича без никаква скорост (липсата на скорост означава покой). Направление на движение през триизмерното пространство = сравнение между две скорости (на подвижния обект и на часовника, с който се отмерват циклите - пясъчен, слънчев, махалов, механичен, електронен, атомен, все едно какъв).
-
За гравитацията видяхме, че не влияе на функционирането на атомите така, както ти си въобразяваш (затова и все още не е открита квантовата теория на гравитацията). Сега да поразчоплим малко и новия бисер - как точно ускорението, на каквото и да било, включително на самите атоми, влияе на вътрешното функциониране на атома (от там - и на атомните часовници)?!!! Тука вече ще тръшнеш на бунището и Ръдърфорд, и Бор, и Фейнман, и Дирак, и Уайнбърг, и всичко, що се е водило квантов физик досега...
-
Да, влияе, но не влияе на вътрешното функциониране на атома, което сие използва в атомните часовници (ако твърдиш обратното - значи си открил толкова търсената квантова теория на гравитацията и ще се радвам да ни споделиш тука откритието си и после да си получиш Нобеловата награда), а влияе съгласно ОТО.
-
Инерционното движение е равномерно-праволинейно движение (отбележи си най-специално - РАВНОМЕРНО). Каква енергия и откъде получава дадено тяло, за да пропада с ускорение (НЕравномерно движение) към Земята? Когато, след няколкостотин години (ако все още си жив), започнеш да осъзнаваш донякъде, какво ти се е писало тук - ще започнеш да зацепваш, че става дума за ГЕОМЕТРИЯ НА ПРОСТРАНСТВО-ВРЕМЕТО и не става дума за никакви въздействия, взаимодействия, механики, механизми, енергии... Дотогава ще си повтаряш като папагал глупостите тука, докато Скенер и Гравити се мъчат да ти налеят малко физическо познание в главата и ще си въобразяваш, че отново си им отговорил много духовито.
-
Я, че ми стана страшно интересно - на какво и как точно са чувствителни атомните часовници, след като НАЙ-СПЕЦИАЛНО пише за тях: "Друго важно изискване към атомните часовници (както и към всеки един часовник) е да е възможно най-нечувствителен към външни влияния (температура, налягане, надморска височина, магнитни и електрични полета и т.н.)." "При другите методи за измерване на време влияние оказват промените в околоосното въртене на Земята, които са известни на учените от векове. През отделните сезони Земята се върти различно и промяната е около една хилядна от секундата. Това прави отклонение от около пет секунди за едно десетилетие. Промените в околоосното въртене не се подчиняват на никакви закони и трудно могат да бъдат предсказани и предвидени. Неравномерността във въртенето на Земята води до отклонение на хода на астрономическите часовници и периодически се налагат поправки във времето, измервано чрез тях. За разлика от тях атомният часовник не зависи от въртенето на Земята." "Точността им е огромна. За много хиляди години те ще се отклонят само с части от секундата. Но дори и тези малки отклонения се дължат по-скоро на несъвършенството и конструкцията, отколкото на промяна в атомната секунда." Атомен часовник – Уикипедия (wikipedia.org) Много ясно, че ще използват атомни часовници за проверка на СТО и ОТО - това е най-точното и най-неподатливо на никакви смущения и въздействия устройство на света, еталон за честота и точност, както е написано. С какво друго искаш да проверяват СТО и ОТО, освен с най-точните часовници?! Ти да не би да си от някоя паралелна вселена, където когато ти пишат, че атомния часовник е най-нечувствителния към външни въздействия и най-точен инструмент - това значи, че ти трябва да твърдиш точно наопаки?! Обикновено това са шизофренни състояния, с тежки халюцинация, до усещане за пълно пребиваване в "паралелни реалности" и се нуждаят от спешно и най-стриктно психиатрично лечение (в някои случаи такива хора могат да бъдат опасни за себе си и околните). И поредното потвърждение, че нещо не ти е наред - пак приписваш на другите (в случая - на мен) твоето повсеместно невежество, не само от областта на физиката, но и въобще от ежедневния живот. Ти когато подкараш колата ти, промениш ѝ състоянието в покой с нулева скорост, не трябва ли непрекъснато да натискаш газта (да изразходваш гориво/енергия), за да поддържаш дори и някаква най-ниската постоянна скорост (например - 5 км/ч)? А защо в Космоса и когато се движиш по инерция с 5 км/ч, и когато се движиш по инерция с 200 км/ч - и в двата случая не изразходваш никаква енергия, за разлика от движението с каквато и да било скорост с колата ти на Земята? Защото ГЕОМЕТРИЯТА НА ПРОСТРАНСТВО-ВРЕМЕТО Е ТАКАВА! Това е направо отчайващо невежество и ментални трудности! Съветвам те да вземеш някакви по-сериозни мерки, защото работата въобще не изглежда на добре...
-
Добре е статията за GPS-ите да се сподели цялата, че е съвсем актуална и е точно за ролята на СТО и ОТО, с конкретни сметки, използвани от истинските инженери, свързани с GPS, не като нашия форумен инженер тук! В кутията: GPS и теория на относителността (9 Октомври 2023 година) Часовниците са в основата на GPS. Напредъкът в космическите атомни часовници, които поддържат времето до 10 наносекунди за един ден, беше ключово развитие, което направи възможно GPS. Оказва се, че GPS трябва да отчита както специалната теория на относителността, така и общата теория на относителността, за да достави на своите потребители позиция на ниво 1 метър и време на ниво 100 наносекунди. Ще използваме тези кръгли числа като очаквания на потребителите от GPS. В простия инженерен анализ по-долу разглеждаме проблемите, които биха възникнали, ако инженерите бяха пренебрегнали теорията на относителността в своя дизайн на GPS. Въпросите, свързани с позиционирането и прехвърлянето на време, са различни, така че ги разглеждаме отделно. GPS всъщност е купчина синхронизирани, почти перфектни часовници в орбита Това е мантра, която си струва да се повтори: за измерване на обхвати до GPS сателити с точност на ниво метър, часовниците на сателитите трябва да поддържат времето с точност на ниво наносекунда. Часовниците на борда на GPS сателитите са изключително стабилни, обикновено до една част от 1013 за един ден, което е друг начин да се каже, че те могат да спечелят или загубят средно 10-8 секунди, или 10 наносекунди, за 105 секунди, което е приблизително дължината на ден. Това е просто изчисление. Да предположим, че измервате времеви интервал от дължина с осцилатор, за който се рекламира, че има честота f, като броите неговите периоди на трептене. Ако действителната честота е (f + Δf), бихте измерили времевия интервал като (T + Δt). Лесно се доказва, че: Стабилността на частичната честота (f / Δf) е ключов параметър. За осцилатор със стабилност (f / Δf) от 10-13 за ден, както е отбелязано по-горе, можем да ограничим средно до 10 наносекунди с качване на данни към сателитите веднъж на ден, за да синхронизираме отново часовниците. Грешка от 10 наносекунди във времето се равнява на грешка от около 3 метра при изчисляване на обхвата и, казано грубо, грешка от около 3 метра в позицията, изчислена от приемника. Можем да живеем с това. Гравитационни и движещи се ефекти върху GPS часовниците Предишното ни изчисление на грешката в отчитането на времето на сателитен часовник щеше да е наред, ако не пренебрегнахме един важен факт: преструвахме се, че часовниците са в покой на Земята на средно морско ниво. И така, нека да видим какво има да каже теорията на относителността за часовниците в кръгови орбити с височина 20 000 километра около Земята. Сателитните орбити не са съвършено кръгли или идентични, но засега нека се преструваме, че са. Ние наричаме това моделиране. Часовниците ще се движат със скорост от около 4 километра в секунда и ще съществуват в среда, където гравитацията на Земята е само около една четвърт от тази на морското равнище. Според теорията на специалната теория на относителността движещият се часовник тиктака по-бавно от този, който е неподвижен на морското равнище. Часовник на борда на GPS сателит ще губи около 7 микросекунди на ден. Това е с три порядъка по-голямо от нашия бюджет за грешка на сателитния часовник, обсъден по-рано, следователно не можем просто да го игнорираме. Според теорията на общата теория на относителността, от друга страна, часовник в по-слабо гравитационно поле ще тиктака по-бързо от този, който е неподвижен на морското равнище. Очевидно гравитацията тежи и на времето. Часовник на борда на GPS сателит в средна земна орбита ще спечели около 45 микросекунди на ден спрямо часовник, който е на морското равнище на земята. Нетният ефект: GPS сателитен часовник ще спечели около 38 микросекунди на ден спрямо часовник в покой при средно морско ниво. Този ефект е светски, което означава, че отместването на времето ще нараства от ден на ден. И така, вие питате: можете ли да ми покажете как стигнахте до тези числа, 7 микросекунди и 45 микросекунди? Не, но мога да ви насоча към препратките, изброени по-долу, и мога да се доближа до тях, използвайки прости математически модели: (i) Гравитационният потенциал на Земята е сложен и за да опростим нещата, ние моделираме Земята като хомогенна по състав и сферична по форма с радиус (rE ) от 6400 километра; (ii) сателитна орбита на aGPS е кръг с радиус 4 rE; и (iii) сателитите се движат със скорост 4 километра/секунда. Спестихме си много проблеми, като се съгласихме на този прост модел. Изчисляването на стабилността на частичната честота (f / Δf) поради релативистичните ефекти вече е лесно и се дава в страничната лента. Отговорите са само приблизителни, но изненадващо близки до числата, цитирани по-горе. Това е красотата на добрите модели. За да изчислите спечеленото или загубеното време за един ден, умножете по продължителността на деня в секунди. Като интересно нещо, имайте предвид, че ефектите, предсказани от специалната теория на относителността и общата теория на относителността, се отменят взаимно за часовници, разположени на морското равнище където и да е на Земята. Помислете за два часовника, единият разположен на северния или южния полюс, а другият на екватора. Часовникът на екватора ще тиктака по-бавно поради относителната му скорост поради въртенето на Земята, но по-бързо поради по-голямото му разстояние от центъра на масата на Земята (около 22 километра) поради сплескването на Земята. Тъй като скоростта на въртене на Земята определя нейната форма, двата ефекта не са независими и не е случайно, че те се отменят точно. Ами ако GPS забрави за относителността? Какво щеше да се случи, ако инженерите, отговорни за проектирането на GPS, бяха пренебрегнали теорията на относителността? Ако GPS сателитите всъщност бяха в идентични, кръгови орбити, техните часовници щяха да покажат озадачаващо, но идентично поведение на печелене на време спрямо часовниците на контролния сегмент на Земята с постоянна скорост, около 38 микросекунди за ден, комбинираният ефект на специалната и общата теория на относителността. Какво би направило това с измерванията на обхвата? Един GPS приемник би измерил обхватите до всички разглеждани сателити като твърде къси с обща стойност (до около 11 километра между ежедневните качвания на корекции на часовника). GPS приемниците обаче не измерват обхвати. За да се измерват обхватите, часовникът на приемника трябва да бъде синхронизиран със сателитните часовници, тежко изискване. Приемниците използват евтини часовници, които се отклоняват и имат честотна стабилност не по-добра от . Приемниците измерват псевдообхвати, т.е. обхвати с общо отклонение поради отместването на часовника на приемника спрямо GPS времето. Това отклонение се оценява от приемника, заедно с неговата триизмерна позиция. Цената на един евтин часовник на приемника е, че сега имаме четири параметъра за оценка и се нуждаем от измервания на псевдообхвата от четири сателита. И така, какво би направило това с позиционирането? Отговорът е, че общото отклонение, въведено от релативистичните ефекти, ще се смеси с обикновено много по-голямото отклонение, въведено от отместването в часовника на приемника. Оценката на позицията няма да бъде засегната. Сега какво ще кажете за времето от GPS? GPS приемник, използван за измерване на времето, обикновено е неподвижен с внимателно проучено местоположение на антената. По принцип, едно измерване на псевдодоранж може да го синхронизира с GPS времето (и UTC). Така че, ако релативистичните ефекти бяха пренебрегнати, точността на синхронизирането щеше да пострада до степен от 38 микросекунди на ден между актуализациите на параметрите на часовника. Това е проблем, като се има предвид, че очакваме точност от 100 наносекунди. Обсъдените досега релативистични ефекти могат лесно да бъдат компенсирани чрез задаване на честотата на сателитните часовници по-ниско (с 0.0045674 херца) в това, което се нарича „фабрично отместване“: Честотата на сателитния часовник е настроена на 10.22999999543 мегахерца, така че да тиктака орбита със същата скорост като атомен стандарт от 10.23 мегахерца на морското равнище на Земята. Какво гениално решение! Това фабрично изместване би отчело напълно релативистичните ефекти, ако орбитите на сателитите на GPS бяха идеално кръгли и идентични. Те не са. Не можете да контролирате идеално орбита. И така, какво ще кажете за ексцентричните орбити? Да, това е усложнение. Всяка орбита е отчетлива и леко елипсовидна. Следствие от това е, че скоростта на сателита не е постоянна (поради втория закон на Кеплер): колкото по-далеч се отдалечава сателитът от Земята в своята елиптична орбита, толкова по-бавно се движи; и колкото по-далеч е спътникът, толкова по-ниско е гравитационното поле. Това означава, че часовниците в различни спътници се ускоряват и забавят по различно време и с различна скорост. Ефектът за всеки часовник е периодичен и квазисинусоидален. Осреднявайки ефекта върху орбита, получаваме нула. За сателит в орбита с ексцентричност от 0.02, нетният ефект е, че часовникът може да бъде напред или назад с цели 45 наносекунди. Съответната грешка в обхвата би възлизала на ± 15 метра. Този ефект трябва да се отчете специално за всяка орбита. Това ще изисква сериозно счетоводство за това къде сателитът е бил в своята елиптична орбита от последното качване на данни, за да синхронизира часовника си. Това е разхвърлян бизнес, но може да бъде опростен. Ще го оставим така. Вижте ICD-GPS-200C, раздел 20.3.3.3.3.1, ако искате да видите как е внедрен във вашия GPS приемник. Относителността е нещо повече от специалната теория и общата теория. Има ефектът на Саняк, свързан с нашите въртящи се референтни рамки, прикрепени към Земята, в които бихме искали да определим позиция. Принципът за постоянство на скоростта на светлината не може да се приложи във въртяща се отправна система, където траекториите на радиолъчите не са прави линии, а спирали. (Приемниците в покой на Земята се движат доста бързо: 465 метра в секунда на екватора.) Съществува и забавянето на Шапиро, свързано със забавянето на електромагнитните вълни, докато те се приближават до Земята, което възлиза на част от наносекунда. Вижте препратките за повече по тези теми. Последна мисъл: Можеше ли Айнщайн да си представи преди сто години, че един милиард души ще отчитат несъзнателно ефектите от неговата езотерична теория в ежедневните си дейности? Референции 1. Ашби (1993), „Относителност и GPS“, колона за иновации в GPS World 2. Ашби (2003),Относителността в глобалната система за позициониране. Живи рецензии в относителността https://link.springer.com/article/10.12942/lrr-2003-1 3. https://www.gps.gov/technical/icwg/ICD-GPS-200C.pdf
-
Напиши му, че това са две Тесли на Мъск, които той е изстрелял да си летят свободно в Комоса преди години и така сега едната си лети по инерция в Космоса по-бързо от скоростта, с която си лети по инерция другата до нея, в едно и също направление. На тия трябва да им описваш всякакви глупави и безсмислени детайли, за да се концентрират над същността и пак не могат да те разберат!!!
-
Прочети цялата статия, де! За да функционира тази ИЗКЛЮЧИТЕЛНО СЛОЖНА система - отчита се ВСИЧКО (и комар някак си да можеше да бръмне в Космоса - и това щяха да се опитват да го отчитат)! Ето ти още един цитат: "In the simple engineering analysis below, we consider the problems that would have arisen if the engineers had ignored relativity in their design of GPS. The issues related to positioning and time transfer are distinct, so we treat them separately." "В простия инженерен анализ по-долу разглеждаме проблемите, които биха възникнали, ако инженерите бяха пренебрегнали теорията на относителността в своя дизайн на GPS. Въпросите, свързани с позиционирането и прехвърлянето на време, са различни, така че ги разглеждаме отделно." Забележи споменаването на ИНЖЕНЕРИТЕ (точно хората на Младенов се занимават с употребата на СТО и ОТО при функциониране на GPS - същите теории, дето Младенов и ти се мъчите да отречете, което очевидно няма как да се приеме сериозно при всички тези постоянно напиращи факти, отвсякъде, за приложението на тези две теории навсякъде)...
-
А ето какво пише тук: Inside the box: GPS and relativity - GPS World "Clocks are at the heart of GPS. Advances in space-qualified atomic clocks that kept time to within 10 nanoseconds over a day were a key development that made GPS possible. It turns out that GPS must account for both special relativity and general relativity to deliver position at 1-meter level and time at 100-nanosecond level to its users. We’ll use these round numbers as user expectations from GPS." "Часовниците са в основата на GPS. Напредъкът в космическите атомни часовници, които поддържат времето до 10 наносекунди за един ден, беше ключово развитие, което направи възможно GPS. Оказва се, че GPS трябва да отчита както специалната теория на относителността, така и общата теория на относителността, за да достави на своите потребители позиция на ниво 1 метър и време на ниво 100 наносекунди. Ще използваме тези кръгли числа като очаквания на потребителите от GPS."
-
Аз въобще не те питам това! Явно, пак ще трябва да ти повторя въпроса, че нещо - много ти слаби реотаните, бавно загряват… Съгласен ли си с моето мнение, че особеностите на движението през три пространствени измерения, които споменахме досега (движението само през едно направление в един и същи момент и поради това - намаляването на движението по една пространствена посока, когато се увеличава по друга пространствена посока) се дължи на геометрията на триизмерното пространство (евклидова, декартова координатна система с три прави лъч, излизащи от един център и разположени на 90 градуса всеки спрямо всички останали) или според теб особеностите, относно които и двамата се съгласихме, са продукт на някакъв механизъм на взаимодействия на обектите в рамките на трите пространствени измерения, без никаква връзка с геометрията на триизмерното пространство, за която вече споменах (може да имаш някакви възражения и относно споменатата геометрия, макар да се съмнявам, защото тя еобщоприета още отпреди Нютон,както и от самия него, разбира се)?