Станислав Янков
Потребител-
Брой отговори
2763 -
Регистрация
-
Последен вход
-
Days Won
1
Content Type
Профили
Форуми
Библиотека
Articles
Блогове
ВСИЧКО ПУБЛИКУВАНО ОТ Станислав Янков
-
Ти какъв реален обект си възприел ДИРЕКТНО, В НЕГОВИТЕ ПЪЛНИ СВОЙСТВА?! Нали ако всяка твоя представа за нещо "реално" беше наистина реална - щеше да се превръща в "реалност" абсолютно всяка глупост, която си помислиш, без изключение?! НИЩО не е реално, а е само по-големи или по-малки (или никакви в твоя случай) мозъчни приближения до реалността. Щом всичко се движи, през времето, а не стои на стоп-пауза (добра функция, ако можехме да спираме на пауза, в реално безвремие, всички писачи на глупости) - как така няма реално време и времето е нищо?!
-
А какво щеше да стане с всичките ти тези описания, ако времето не беше реално и го нямаше, ако беше нищо? Изведнъж процесът, който така последователно обясняваш, щеше да замръзне на вечна пауза, на едно и също място в трите пространствени измерения и както налягането се увеличава - ще престане да се увеличава, намалява, променя, в каквото и да било направление в пространството, за веки веков... Успяваш ли да осъзнаеш, каква глупост се опитваш да пробуташ с твърдението ти, че движението по трите пространствени измерения е реално, а това по времевото измерение - нереално?!!! Самият факт, че го изписваш това нещо, във времето, показва, че има време и че то е съвсем реално - ти не си в безвремева стоп-пауза.
-
Абсолютно всяко човешко съждение, от всяко естество, даже и наглед най-най-най-супер-дупер-"сигурното", е формално. Цялата продукция на човешкия мозък е именно това - въображаеми, мисловни конструкции (визуалните картини са същото - те не показват дори инфрачервените и ултравиолетовите отражения/лъчения, макар това да са си съвсем пълноценни електромагнитни вълни, заедно с видимия спектър), които изграждат някаква картина (не винаги научна) на света и на съществуването и вземат решения и провокират действия въз основа на мисловната личност. Изчакай две нереалности (два часа) и си пусни един студен душ - да се поосвестиш малко и по някакво чудо мозъка да позаработи малко по-чевръсто, че сега едва движи, стърже, скърца, хлопа... Я кажи, щом времето е нищо, нереално - защо продължава да протича с неговите интервали, дори и когато не се местиш по никоя от трите пространствени координати (например - седиш си отпуснат във фотьойла в стаята и си дремваш)? Когато едно нещо е нереално, то не може да протича със съответните отрязъци, даже и когато не се движиш (илюзорно) през пространството, защото то е НИЩО, НЕРЕАЛНО! Нищото, нереалността не се движат, камо ли пък непрекъснато, нали?
-
Всички физически закони (включая нютоновите) правят точно същото. И са си били екстра много дълго време, преди да бъдат заменени от релативистките зависимости (не изцяло - някои нютонови положения си работят без замяна и до ден днешен). Те самите са заменили Боговете, ангелите, демоните, въобще - "небесните сили", които според човечеството дотогава управлявали ВСИЧКО! Още по-готиното е, че няма алгебрична зависимост, на която да не можеш да съставиш геометрична форма като аналог. Това са две тясно свързани и взаимопроникнати аналитични форми, които могат да се присвоят буквално на всичко (включително и на изцяло въображаемото - като глава и рамене и другите графични фигури във форекса, за които споменах в по-ранен коментар тук). Всичко, което можеш да опишеш алгебрично - можеш да опишеш и чрез някаква подходяща геометрия и въпросът е само в намирането на най-подходящата и най-добре пасваща геометрия...
-
Ако не можем да се съгласим - значи някой от двама ни бърка и е нужен безпристрастен арбитър, който са останалите тук. Просто те питам за аргумент, защо времевата координата да е по-нереална от нереалните пространствени координати? Това не е някакъв драматичен конфликт или нещо подобно, само си изясняваме - кой какво точно има предвид. Решавам го, защото когато измервам дължина - измервам първа измерност, когато измервам широчина - измервам втора измерност и когато измервам височина - измервам трета измерност. Когато измервам времева продължителност - измервам нещо различно от останалите три случая, затова значи измервам четвърта измерност. Температурата е резултат на поведението на излъчващите материали и на излъчваните от тях електромагнитни вълни (те са температурното въздействие) в пространство-времето (четирите измерения). Температурата е последващ продукт на поведението на материята по четирите измерения на пространство-времето и няма смисъл да е допълнително измерение - не дава допълнителна степен на свобода.
-
Добре, де! Решихме, че трите пространствени измерения не са реални, а са само описателно пособие на реалността (същото е и приемането на времевата координата като измерение). По това вече няма спор - този момент е приключен. Въпросът е - въз основа на какво твърдим, че нереалното времево измерение е по-нереално от нереалните три пространствени измерения (които са само геометричен/математически модел за описание на реалността)? Между другото - снимката също е нереална, колкото и да се доближава до реалността, която заснема, защото е само изображение, а не е самата реалност…
-
Добре! Значи точната дефиниция е, че измеренията (координатите на измеренията) не са реални, а са само геометрични/математически похвати/средства/модели за описание на реалността. Тук мисля не само аз, но и всички останали ще се съгласят. Сега - следващия въпрос! Ако трите пространствени измерения (координатите им) не са реални - как решаваме, че координатата на четвъртото времево измерение е по-нереална от координатите на трите нереални пространствени измерения?! Няма нужда излишно да уточняваме, че и представата за пространствени измерения, и представата за стрела на времето, са продукт (по-вярно или по-невярно дефинирани аспекти) на материята и на начините, по които материята се движи/променя - това се приема, че се подразбира.
-
Младенов, искаш ли първо да престанем да шаткаме в твърденията и да уеднаквим и стабилизираме понятията? В няколко различни твои поста ти твърдиш за едни и същи неща противоположни работи. Веднъж твърдиш, че трите пространствени измерения са реални (не са - и те са виртуални като времевото, защото не можеш да покажеш на Скенер някое от трите пространствени измерения, което да си препуска сам-самичко нанякъде), а втори път твърдиш, че геометричните/математическите измерения (пространствените са също такива, както и времевото) са модел на реалността, а не самата реалност. Кога си прав? Когато твърдиш, че трите пространствени измерения са реални или когато твърдиш, че всички измерения, включително и трите пространствени, не са самата реалност, а са само геометричен/математически модел на реалността?!
-
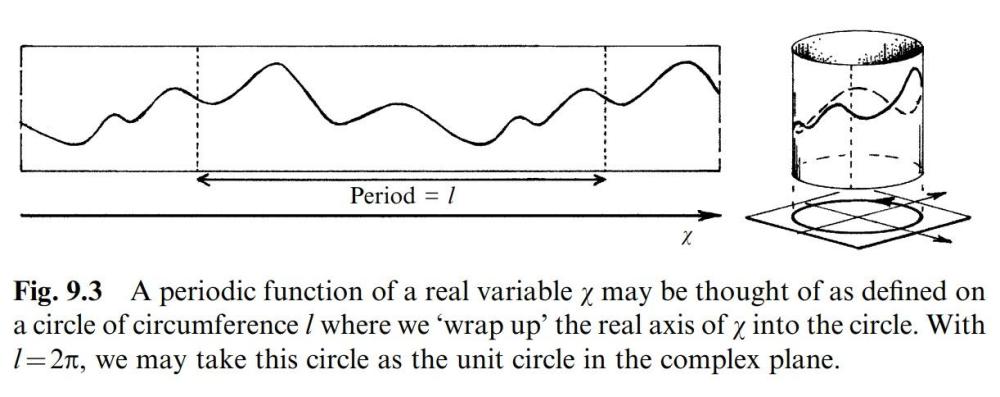
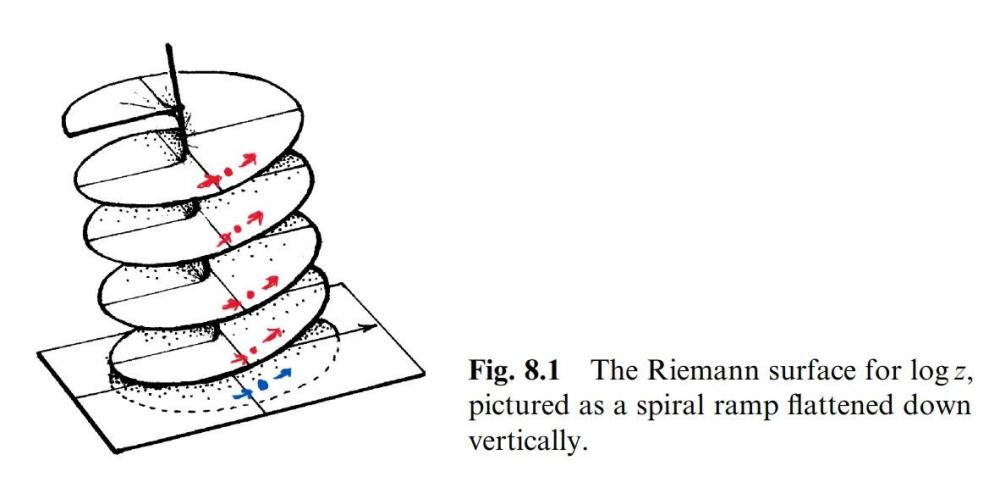
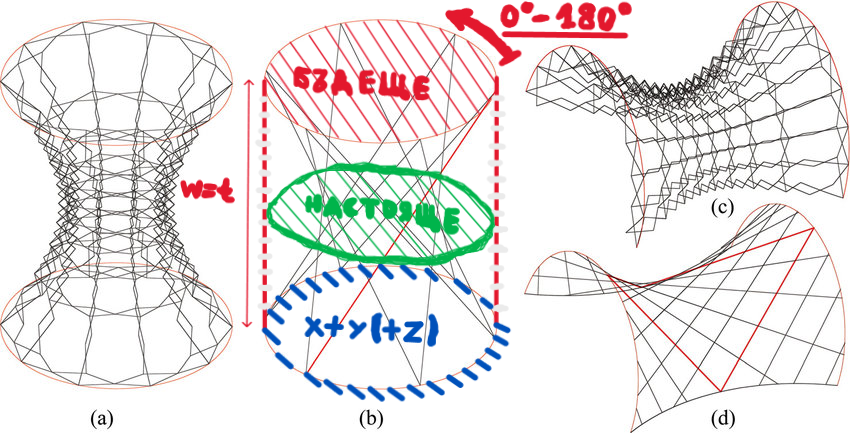
На следващото изображение е дадена функция върху окръжност (това е част от разлагане на ред на Фурие - многообразията са още по-сложни от това): Отдолу имаме двуизмерна плоскост с кръг, който обаче върху цилиндър по трето измерение всъщност се оказва много по-сложна форма. Ограниченото двуизмерно възприятие пречи да се възприеме по-сложното триизмерно представяне по по-различен начин от правилен кръг. На следващото изображение е даден условен начин на "разтягане" на двуизмерната повърхност на триизмерна сфера като две плоски, разтегнати измерения. Който може - да направи аналогия с четиримерна хиперсфера, три от измеренията на която са разтегнати до трите плоски, прави, разгънати, безкрайни пространствени измерения на познатата ни Вселена. На следващото изображение са дадени две измерения, навити на спирала, които се представят припокрити като едно нещо върху двуизмерния плосък екран отдолу: Червената точка прави големи кръгове по спиралата, като на всяка следваща намотка е съвсем леко изместена спрямо предишната и голям брой намотки по третото измерение нагоре са натрупани в едно "макроскопично" синьо изображение на точка върху плоския екран отдолу. Сега можем да си дадем сметка, че двете измерения, които се увиват по спирала и насложени дават плоския екран отдолу, са всъщност три пространствени измерения, а височината на третото измерение, по което се увиват спираловидно двете други пространствени измерения, всъщност е четвъртото пространствено измерение на Минковски (времето), по което се увиват трите обичайни пространствени измерения на Вселената. Понеже нашето човешко съзнание не е с достатъчна разделителна способност - ние не можем да възприемем отделните навивки на трите пространствени измерения нагоре, по четвъртото измерение, а ги възприемаме като определено количество насложени една върху друга, под формата на плоския екран с макроскопичната точка отдолу. Понеже реално при всяка следваща намотка червената точка е леко изместена в сравнение с всяка предходна точка, което е извън нашата разделителна способност - ние приемаме този детайл като вълни на неопределеността на макроскопичната синя точка върху насложения екран отдолу. Способността на разделителната способност (теоретичната) да отрази преместване по макроскопичния триизмерен екран отдолу (броя насложени една върху друга по четвъртата ос на времето намотки, които се "порожектират" в един и същи момент, като планкови размерности, върху триизмерния екран на вселенското пространство отдолу) се определя чрез вълните на неопределеността на Де Бройл. Това е моята представа за момента относно четирите измерения на пространство-времето (естествено - ще търпи развитие и усъвършенстване в бъдеще). Кой разбрал - разбрал! Който не разбира - да си спори, колко си ще!
-
Може би не работят пълноценно всички мозъчни неврони... Например, когато търгуваме форекс на различните пазари, практиката при техническия анализ от много години е доказала, че най-добре боравим с визуална информация - представяне на поведението на цената с времето върху графика, с графични фигури (двойни, тройни върхове и дъна, триъгълници, глави и рамене и обърнати глави и рамене, клинове, флагове и други подобни). Дау-теория, вълнова теория, прайс-екшън - ВСИЧКО тука е графични фигури на цената с времето върху визуални диаграми! Да, ама кога реално сме виждали цената на някой търгуван на борсите продукт под формата, примерно, на глава и рамене?! Никога и никога и няма да го видим, което не ни пречи да представим поведението на цената върху графика в подобна форма в някои случаи и това поведение е било съвсем реално, след като е отчетено по този начин на графиката. Ето затова такива като Младенов нямат никакви шансове на глобалните борси и моментално ще фалират - тежък интелектуален недостиг!!!
-
Най-актуалния и най-добре работещия геометричен модел, свързан със СТО, е модела на Минковски. Остави старите неща (по времето на Нютон дори не са знаели за всички ефекти, описвани чрез СТО и ОТО, а преди Нютон не са знаели и за нютоновите закономерности и са обяснявали всичко с богове, ангели, демони, джинове и т.н.) и състави по-добър модел от този на Минковски (експерименталните потвърждения на твоя по-добър модел няма да оставят никакво съмнение в неговото преимущество над досегашните разработки).
-
Обясни детайлно и безспорно, защо с промяната на скоростта на движение между теб и други обекти се променя и темпа на осцилациите, които броиш при твоя и при техните часовници? Каква е причината да съществува и да се отчита експериментално тази взаимозависимост, след като по Нютон не би трябвало да съществува? Кое е по-доброто обяснение от това на Минковски (отричането на експериментално потвърдения ефект не е обяснение)?
-
Разбери нещо! НИЩО от това, което виждаш, чуваш, усещаш, разбираш и т.н. не е ДЕЙСТВИТЕЛНАТА реалност (до нея никой няма пълен достъп, освен може би Бог, ако съществува). Дори ако вземеш зрението - ВСИЧКО е твои мозъчни, мисловни конструкции, които ти формираш въз основа на светлинните дразнения, предавани чрез очите (и това също е модел, абстракция, по която си мислим, че стават нещата), но НИЩО от всичко това НЕ Е действителната реалност, до която никой от нас няма пряк достъп. Щом се налага степен на свобода, по която материята да се проявява, за да опишеш смислено проявлението, до което е успяло да достигне съзнанието ти в днешно време - това е четвърто измерение и е като всички други измерения, дори когато има разни разлики в детайла. И без проблеми може да се представи като някакъв геометричен модел (видим или невидим за нашите очи и други сетива, както не виждаме инфрачервената и ултравиолетовата светлина). Ние използваме всякакви модели - геометрични (който така иска), математически (който така иска), други (който така иска), комбинирани в най-различни съчетания (който така иска) - но всичко това са ПРОСТО МИСЛОВНИ МОДЕЛИ и НЕ Е ДЕЙСТВИТЕЛНАТА РЕАЛНОСТ.
-
А въз основа на какво решаваш, че зрителната (геометричната) интерпретация е по-важна или по-маловажна от математическата интерпретация?! Всичко това са различни средства за осъзнаване от човешкия интелект (осъзнатост) на различните проявления на материалните особености. Дали ще избереш зрителна, геометрична, графична, математическа интерпретация - няма никакво значение, след като всяка от тези различни форми ти помага да си формираш някакви модели на проявлението на вселенската материя пред твоето съзнание! Зрителните ти възприятия също са абстракция (зрителна) и не са действителната реалност, до която никой няма пълен достъп (ти дори не улавяш инфрачервената и ултравиолетовата светлина, какво остава пък за неизвестния брой други неща от реалността, за които дори не можем и да се досетим).
-
Ти бълнуваш ли нещо, човече?! Къде го виждаш това пътуване в бъдещето, особено пък когато не съм спирал да пиша, че ние перманентно се намираме само в настоящето (като осъзнатост/мозъчни процеси на съзнанието)?! Явно вече забрави за конусите на миналото и на бъдещето на Минковски, с точката на настоящето в центъра им! Последните дни, нещо, съвсем си свалил нивото - до смущаващи дъна!!!
-
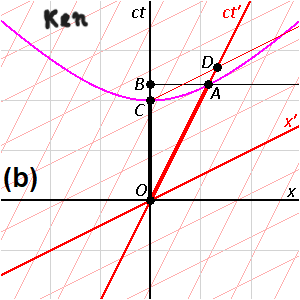
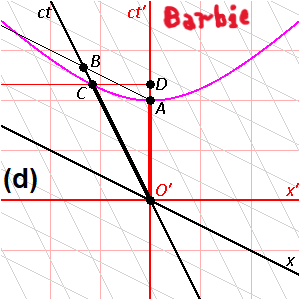
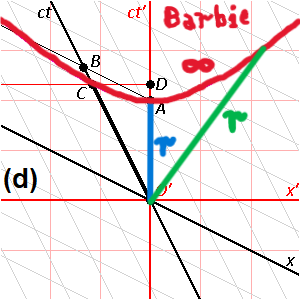
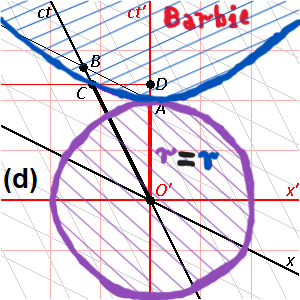
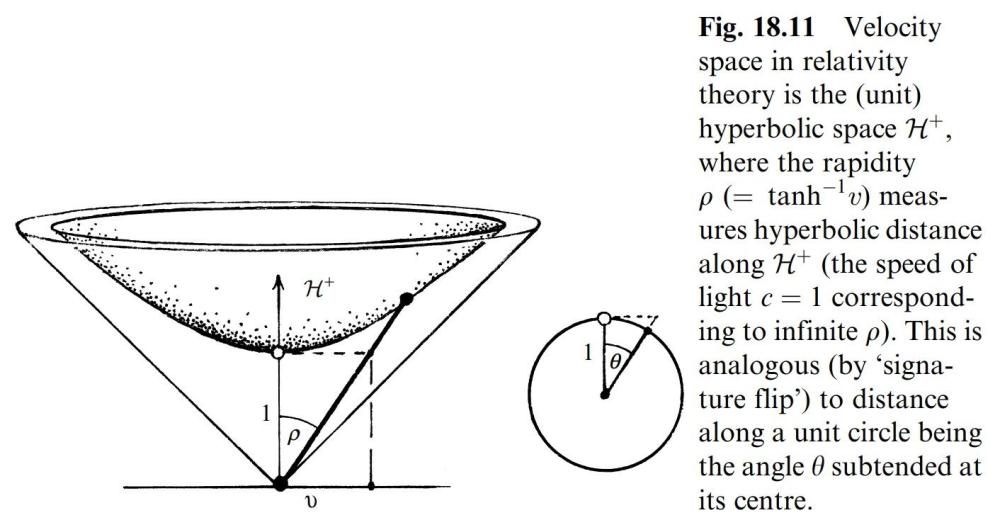
Това не е задължително и дори обратното! Виждал ли си тръба, на която отвора в единия край е много голям, можеш даже да се разхождаш в него, а в другия край е много малък, толкова малък, че и карфица не можеш да промушиш (но го има)? Нищо не забранява и такова обяснение (нали самия Младенов казва, че лоренцовите трансформации могат да се интерпретират по много начини?)! Самият Младенов казва, че Минковски дефинира хиперболична ротация в четиримерно пространство. Ако всичко с движението на материята по четири измерения беше обичайно - щяхме да имаме най-обикновена евклидова, обичайна кръгова ротация през споменатите четири измерения и линейни, а не хиперболични зависимости (по-специално - пропорции). Да, но ротацията е хиперболична (хиперболичен кръг) и това е свързано с редица ефекти, сред които и огъване на правите линии, както и така да се каже "разтягане" (понеже могат да се правят всякакви "манипулации" с измеренията, в зависимост от формите и скоростите на движение на съвкупната материя през тях, но връзките между измеренията не могат да се "разкъсат"), а причината е някаква диспропорция между движенията на материята по измеренията, която при това не се отнася само до трите и четвъртото, а може да се отнася до всички четири измерения едно спрямо друго (между трите измерения помежду им диспропорциите са нерегистрируемо по-малки от диспропорциите между трите и четвъртото измерение). Помисли си само, как е възможно енергията на една масивна елементарна частица, произтичаща от формулата на Айнщайн за масата и енергията, да е "затворена" в пространство с точков (нулев или максимум планков) размер. Ето едно изображение, което бях поставил по едно време (иде реч на "завъртане", "разтягане", хиперболична ротация на координатните системи на движещи се с някаква досветлинна скорост обекти един спрямо друг):