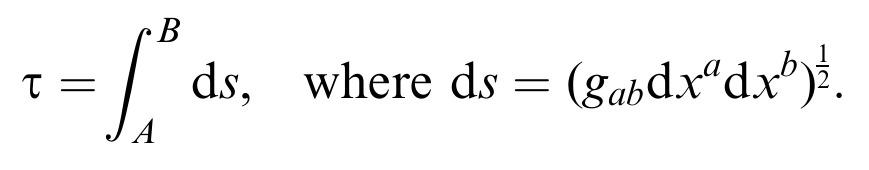Станислав Янков
Потребител-
Брой отговори
2763 -
Регистрация
-
Последен вход
-
Days Won
1
Content Type
Профили
Форуми
Библиотека
Articles
Блогове
ВСИЧКО ПУБЛИКУВАНО ОТ Станислав Янков
-
Съжалявам, че ще ти опонирам толкова категорично, но - това, което не разбирам ясно, въобще не е елементарно и очевидно и уж да няма нищо сложно и тънко! Ето тук вече си противоречиш с малко по-горе и даже и да обясниш по-обстойно защо все пак си прав и в двата случая - това със сигурност няма да бъде елементарно и очевидно обяснение!
-
(0) при неподвижност, покой, няма посока. (+) за приближаване и (-) за отдалечаване. Която и отправна система да се избере за покоящата - всички останали системи или се приближават, или се отдалечават спрямо центъра и'. Всякакви произволни посоки на векторите в 3D-пространство могат да се дефинират до това положение, посредством питагоровата теорема. И посоката на лъч светлина може да бъде всякаква в 3D, без това да пречи скоростта на светлината във вакуум да е инвариант, при това - спрямо всички координатни системи едновременно, даже и при силна гравитация (тогава не се променя скоростта на светлината, а нейната честота/дължина на вълната). Защо възможността вектора на скоростта да бъде насочен навсякъде в 3D-пространство да елиминира това, че стойността и даже знакът му при определен тип разсъждения са еднакви от гледна точка и на двете подвижни една спрямо друга системи?
-
То дори знаците + и - са условни. Всеки от два отдалечаващи се обекта счита себе си за неподвижен и другия за отдалечаващ се, значи така всеки от двата обекта може да определи скоростта на другия като (-v). Ако двата обекта се приближават един към друг - всеки от двата ще счита скоростта на другия като (+v). Подобно, при примера с координатни стойности (0,0), (2,1) и (4,0) интервалът s на неподвижната система ще е 4, а на движилата се до (2,1) и после обратно до (4,0) ще е приблизително 3,4641 (по-къс). Колкото и просто да е за разбиращите - на мен не ми е чак толкова просто и въобще не е толкова лесно за разбиране.
-
За да не се отклоняваме излишно, аз просто употребих един пример от втора страница в тази тема, където с Ники се обсъждаше въпросът с "по-кратък път през пространство-времето". Ето накратко написаното около примера тогава: До тук ли я докарахме? Да не може да извадиш 1 от 1? Малийййй..... Гравити само леко е допуснал движение със скоростта на светлината , но това не променя схемата, само по-лесно се смята. Ами интервалът, резултат от сметките, дава собственото време за пътуващият. И то е НУЛА. При това положение той се движи със скоростта на светлината. Мисля че е съвсем ясно. Формулата е s^2=(ct)^2-x^2 , тоест първата координата е t, втората е x. Значи се разглеждат две отсечки в ПВ: - от (0,0) до (1,1); - и от (1,1) до (2,0). Демек, по времето, първо се върви от 0 до 1, после се върви от 1 до 2, няма назад по времето. А вече и по двете отсечки пътят в ПВ е нула, независимо че пътят в пространството е от 0 до 1 и обратно, тоест общо 2. Но това е в системата на другия наблюдател, приет за неподвижен. Удобно е да описваме от този наблюдател, защото другият се движи със скоростта на светлината и за него всичко е нула, за да се получи и интервалът нула. НО, ако вторият не се движи със скоростта на светлината (за да вложим физически смисъл в наблюдателя и измерителната му система), а маааалко по-бавно, пак ще получим ПВ интервал близък до нулата, силно различен от 2, какъвто е за неподвижния наблюдател. Което показва, че в зависимост от характера на мировата линия интервалът намалява спрямо стойнстта му за неподвижен наблюдател. Което и лежи в основата на "парадокса" на близнаците Идеята беше да е лесно и бързо за смятане, а след като вече веднъж е коментирано - да не се отклоняваме с маловажните моменти (като например, че нищо масивно не може да се движи със скоростта на светлината във вакуум). Иначе, ако трябва да се търси нещо по-прецизно - или говорим за наблюдател с фенерче, който в (0,0) излъчва светлина към огледало, в (1,1) светлината се отразява от огледалото и в (2,0) се регистрира от излъчилия я наблюдател, или въобще трябва да сменим примера с нещо от сорта на два неподвижни обекта в (0,0), единия остава неподвижен до (4,0), а другия първо минава през (2,1) /това е движение с половината от скоростта на светлината/ и след това се връща /пространствено, не да се връща назад по времето/ до (4,0). И на тези примери пак могат да се намерят купища кусури (малко масивни неща се движат 0,5с, главно елементарни частици, светване с фенерче не във вакуум няма да дава скорост 1с, на светлината от фенерчето не може да се припише примова координатна система и какво ли още не). Не в тези детайли е смисъла на въпроса и исках да избегна забатачване в тях, но - както и да е... Сега ще разгледам по-внимателно всичко, което Скенер и Шпага написахте и показахте и чак след това ще отговоря.
-
Добре! С това се бъркам отдавна, затова - да видим, откъде идва това объркване! Ще използвам примера на Гравити от стария разговор с Ники, защото е прост и прегледен. Формулата за пространствено-времевия интервал при този пример е следната: s^2=(ct)^2-x^2 Имаме точките (0,0) и (2,0) и координатната система на наблюдателя (да я наречем система А) е неподвижната в пространството, по формулата получава пространствено-времеви интервал s=2. Друга система (система В) се движи със скоростта на светлината (според примера) първо от (0,0) до (1,1), а след това до (2,0) и тогава формулата дава интервал s=0. Ако за всички системи интервалът може да има една и съща стойност - значи едната от двете стойности s=2 и s=0 не представлява пространствено-времевия интервал. Коя е тя и защо? Ето тук някъде се чупи разбирането ми! Началната и крайната точка (събитията "разделяне" и "среща") са ясни.
-
Събитията/точки са налични и в двете системи. Нали не греша, че пространствено-времевия интервал между тях може да бъде с различна стойност, в зависимост от коя система се оценява (2 за S1 и 0 за S2 в конкретния пример)? Интервалът е тясно свързан с мировите линии между двете събития/точки (той е собственото време Тау, умножено по скоростта на светлината, която е константа - собственото време дава разликите), а мировите линии могат да бъдат с различни дължини.
-
В другите случаи инвариантността може да се разграничи на два различни типа - тази на скоростта на светлината във вакуум (и на законите на физиката по-общо), която е с една и съща стойност за всички наблюдатели и във всички ситуации и тази на пространствено-времевия интервал, където при две системи S1 и S2, ако за едната система S1 дължината на интервала е равна на 2, а за другата система S2 дължината на интервала е равна на 0 (примера на Гравити към Ники някога, от 2-ра страница на тази тема) - и двете системи ще считат, че интервалът на S1 е 2 и на S2 е 0, няма алтернативни показания, както с t и t` и L и L` при движение на системите с някаква скорост помежду им. Това би трябвало да означава инвариантността на пространствено-времевия интервал. По същия начин, при скоростите, ако системата S1 регистрира, че се отдалечава от системата S2 със скорост 100 м/с, то и системата S2 също регистрира, че се отдалечава от системата S1 с точно същата скорост 100 м/с. Същото важи и ако двете системи се приближаваха, вместо да се отдалечават, както и за резултата от лоренцовото събиране на скоростите (няма основен и примов резултат, както няма и въобще основна и примова скорост, за разлика от t/t` и L/L`, нито при покой между системите едната да смята скоростта между двете за 0 м/с, а другата - за някаква различна). Това би трябвало да означава, че и скоростта на движение между инерциалните системи е инвариантна величина, точно така, както е инвариантна величина и пространствено-времевия интервал - и при двете няма основна и примова стойност в зависимост от движението, за разлика от t и L, където има примови стойности, зависещи от темпа на движение между системите.
-
Много интересно! Постоянно се подчертава инвариантността спрямо всички инерциални отправни системи на ред параметри, свързани със СТО - на физическите закони, на скоростта на светлината във вакуум, на пространствено-времевия интервал S, на собственото време Тау и т.н. В същото време - напълно се подценява (не се споменава подчертано) и игнорира инвариантността на скоростта на движение между инерциалните системи (всички инерциални отправни системи са съгласни, че скоростта и резултатът от лоренцовото събиране на скоростите са еднакви за всички)!
-
Може би по-скоро се дължи на естеството ѝ на педантична германка - стреми се да се отнася сериозно към всеки клип и казваното в него, подобно на авторитетен коментатор на сериозни новинарски емисии от голям телевизионен канал (смешките и шегичките са в по-леките и непретенциозни шоута). Опитва се да влага в изявите си и някакви елементи на хумор (например - разрошването на косата в този клип), но и те са до голяма степен суховати и схванати, в типичен германски стил.
- 82 мнения
-
- време
- гравитация
-
(и 2 повече)
С тагове:
-
Принципно и едното времево измерение на стандартното пространство-време е част от симетрия (Лоренцова група симетрии). Защо смяташ, че като са повече членовете с противоположен знак - това прави закономерностите с тях идентични със свързаните с пространството? Какво забранява при противоположния знак да има противоположна на пространствената проява (примерно - там обратния квадрат да е свързан със събиране, вместо с разреждане или нещо друго подобно)? Впрочем, за какъв вид симетрия въобще става дума тук, има ли някаква яснота? (Пенроуз има обосновка срещу повече от четири реални измерения, но тя е доста по-различна от твоята, включва употреба на кардинални числа и разни други съображения.)
- 82 мнения
-
- време
- гравитация
-
(и 2 повече)
С тагове:
-
И понеже дори и едното времево измерение не участва в разреждането (законът дава брой три, а не четири на измеренията, в рамките на които протича разреждането, следователно тук времевото измерение не фигурира) - можем да имаме и повече от едно времево измерение, като всичките, бидейки времеви, няма да участват в закона за обратните квадрати, точно както не участва и едното (времевото или времевите измерения се проявяват по различен начин от пространствените).
- 82 мнения
-
- 1
-

-
- време
- гравитация
-
(и 2 повече)
С тагове:
-
И моето е шега! Засега не съм сигурен как точно безспорно изцяло въображаемата картина на света, която ни осигурява мозъка, се взаимосвързва с абстракцията "реалност", но за момента ми се струва, че става дума за честоти и техните влизания и невлизания във фаза и противофаза (всички елементарни частици, включително и масивните, включват в описанието си и вълнови характер). Пространствените отстояния пък в основата си започват от принципа за забраната на Паули (невъзможността фермионите да заемат едно и също място в пространството или казано по друг начин - всичките им квантови числа да са еднакви). Всичко това, отгоре-додолу, са наши, човешки въображаеми представи. Един камък по никакъв начин не усеща и не може да разбере, че стои неподвижно на някой зъбер или се търкаля по нанадолнището (даже не може да осъзнае самото си съществуване - липсват му нужните сетивни и мисловни инструменти). Ние сме тези, които даваме, във въображението си, всички тези описания на всички останали неща, както и на нас самите (пак намигване към Младенов).
- 82 мнения
-
- време
- гравитация
-
(и 2 повече)
С тагове:
-
Ти сам си го написал - постоянна скорост ВЪВ ВРЕМЕТО. Времето ти трябва, заедно с посоката, като неизбежен параметър за определянето на начина на разпространение. Различните темпове на часовниците в зависимост от наблюдателите не променят постоянното наличие на причинно-следствената връзка (на една-единствена посока на Стрелата на времето - неотменимостта на посоката на ентропията винаги от по-голяма към по-малка подреденост).
- 82 мнения
-
- време
- гравитация
-
(и 2 повече)
С тагове:
-
По това даже съм свършил работата! И времето, и пространството са въображаеми продукти ("пространството и времето са илюзии", "това са примитивни представи"), те не са нищо друго, освен въображаеми конструкции на нашия мозък, така че - в същността се всичко това е чисто и просто ВЪОБРАЖЕНИЕ! Отдавна съм споменавал това и след като обилно ми се накарахте, че го пиша (не било физика и т.н.), явно го забравихте!
- 82 мнения
-
- време
- гравитация
-
(и 2 повече)
С тагове:
-
Аз казвам, че глупост или не самият реферат (там има и други аргументи срещу реферата, освен критикуваните от мен), тези, че електромагнитното и гравитационното взаимодействие (въздействието им) се разпространяват в триизмерна пространствено среда не се отразяват на допускането, че може да има още две допълнителни ВРЕМЕВИ, НЕ ПРОСТРАНСТВЕНИ, измерения. Наличието на две допълнителни времеви измерения не значи, че трябва да има и още едно или две допълнителни пространствени измерения (в текста на критикувания материал специално е отбелязано, че пространствените измерения са си три), за да се излъчва като критика срещу материала такава срещу повече от три ПРОСТРАНСТВЕНИ измерения. Няма нищо общо между написаното от автора на тоя материал (шест измерения, от които три времеви) и моето предположение за асиметрия между протяжностите по три пространствени от една страна и по четвърто пространствено от друга страна измерения (още не съм сигурен, дали мога коректно да пренеса тази концепция и към степените на свобода - те да са само три транслационни и четвърта ротационна, вместо настоящите шест). Освен това още нямам яснота, дали при четвъртото пространствено при мен измерение става дума само за съкратена пространствено, но все пак линейна форма (частта а) от долното изображение) или за увита форма (частта b) от долното изображение). Обичайният темп на часовниците в покой (максимално-бързият възможен) се регистрира както от часовници вътре в движещ се с постоянна скорост спрямо външни наблюдатели обект (часовниците вътре в обекта се считат за неподвижни спрямо него), така и от часовници вътре в обект, който се ускорява гравитационно по геодезична линия. Така ние бихме отчитали обичайния часовников темп на часовник в покой до нас и когато се движим равномерно праволинейно, с почти 1с, изцяло по координатата w на четвърто пространствено измерение и пространственото отстояние по направлението на това измерение спрямо нас е съкратено лоренцово до планковата дължина, и когато се движим по кръгово направление по същата тази координата на w, което е вид движение с ускорение и е аналог на свободно гравитационно падане към масивен обект, по геодезична линия. Тука трябва да намеря някакъв достатъчно сигурен признак, за да изключа единия от тези два варианта. Що се отнася до метриката, която се ползва в ОТО и СТО - та има следния вид: Степента 1/2 накрая означава, че изразът в скобите се намира под корен квадратен (ако беше 1/3 щеше да значи, че става дума за корен от трета степен) и цялото това нещо идва от симетриите. Например, симетрията на сфера би могла да бъде означена по два различни начина:
- 82 мнения
-
- време
- гравитация
-
(и 2 повече)
С тагове:
-
Да, из пространството и според пространствено-времевата парадигма това пространство е тримерно. По него можеш да избираш движение напред по дадено направление е след това в обратната посока, назад, а по условното времево направление назад не можеш да се връщаш, там направлението е само едно и необратимо (причинно-следствената връзка), независимо от разликите в темповете в зависимост от релативистките ефекти. При бухване на ракета в черна дупка, когато ти, наблюдателя, си на безопасно място от нея, ще гледаш само остатъчното изображение на бухналата се в дупката ракета и това изображение ще "навлиза" в дупката много-много години, докато накрая не избледнее (преди въобще да е "потънало" в хоризонта на събитията на дупката). Ако пък си в бухналата се в дупката ракета - нещата ще са коренно различни... Всичко това не променя факта, че според пространствено-времевата интерпретация ефектите на електромагнитното и гравитационното взаимодействие се разпространяват в 3D-пространство, в течение на времето (тука "разпространението" е винаги само в едно направление - от минало към бъдеще, причинно-следствена връзка).
- 82 мнения
-
- време
- гравитация
-
(и 2 повече)
С тагове:
-
Всичко е свързано, но не всичко се проявява по еднакъв начин. Зрението е двуизмерно, наблюдаваме посредством едно двуизмерно екранче, една амбразурка, без да си завъртим главата не можем да видим дори какво е отляво или отдясно, срещу ушите ни, камо ли пък срещу задната страна на черепа ни. Въпреки това можем да избираме направление на движение в триизмерна околност (напред-назад, наляво-надясно, подскок нагоре или скок надолу в пропаст) и осъзнаваме триизмерността на възприеманата чрез зрението ни картина, като приписваме на наблюдаваното и "дълбочина" (проективното представяне, при което нещата се свиват, намаляват размера си, колкото по-далече са от нас). Когато сме плътно фиксирани в някаква тръба и ни преместят по нея, разглеждането може да бъде и само едномерно. Всичко е свързано, но може да е свързано посредством доста сложна геометрия, при която материалните процеси по направленията на различните измерения се изявяват пред особеностите на човешката мисловност и сетивност различно, а човешката мисловност и сетивност е основния фактор, който играе роля в изграждането на нашите научни модели. Силата не се разпространява по времето (условното четвърто НЕпространствено измерение при пространство-времето), а с времето. Разпространява се само в рамките на трите пространствени измерения и особеностите на това разпространение се оценяват в течение на времето. Аз се опитвам да разработя четиримерна пространствено алтернатива на пространствено-времевата концепция (без да отричам потвърдената до момента коректност на последната), но това е съвсем друго нещо. В пространство-времето ефектите на взаимодействията се разпространяват само в рамките на пространството, с течение на времето.
- 82 мнения
-
- 1
-

-
- време
- гравитация
-
(и 2 повече)
С тагове:
-
Електромагнитното и гравитационното въздействие (силата му) в този случай произтича от двумерна сферична повърхност и при 1/R^2 (при три пространствени измерения) посоките се мащабират с повърхността на сфера, затова R е на квадрат (така го е обяснила Сабине в клипа). Имаше и един клип на PBS Space Time, където това беше показано и по-нагледно. Аз изхождам, че след като става дума за допълнителни времеви, а не пространствени измерения - по-уместно е да очакваме тяхното присъствие или отсъствие да се установява посредством времеви особености/"аномалии", а не посредством пространствени такива и при това във връзка с евклидово, макроскопично пространство. Иначе, в клипа си Сабине е добавила още съмнителни моменти и тези критики вече изглеждат доста основателни.
- 82 мнения
-
- време
- гравитация
-
(и 2 повече)
С тагове:
-
Не бързай толкова! Сабине само казва, че допълнителните две времеви измерения не са нормални пространствени измерения - по тях няма разпространение на силовите линии (спектрално измерение), а електромагнитната и гравитационната сила от сферичен източник спада по формулата 1/R^2, което потвърждава триизмерно ПРОСТРАНСТВО (ако беше двуизмерно, работещата формула щеше да бъде 1/R^1, а при четириизмерно - 1/R^3). Да, обаче в предположението се говори за три ВРЕМЕВИ, не за допълнителни над трите пространствени измерения. Материалът може да има куп слабости, включително и фатални, но тази част от критиката на Сабине е прибързана.
- 82 мнения
-
- време
- гравитация
-
(и 2 повече)
С тагове:
-
Тава трябва да важеше само за взаимодействия между елементарни частици. Разширението на Вселената и аналогичният на това Доплеров ефект не са това и там съображенията за квантуване (порционизиране?) не са приложими. Там можем само да правим заключения, дали енергията на лъчения, излъчени от много далечни частици, ще е достатъчна да предизвика ефект в атом и в неговите елементарни частици (най-често електроните).
-
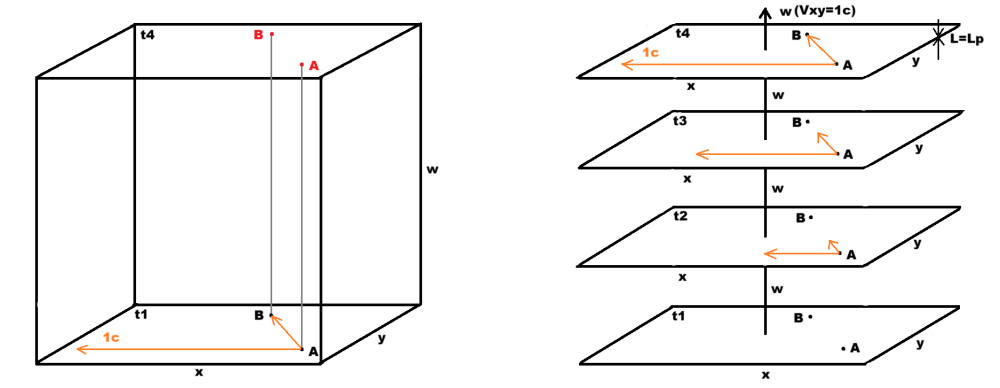
Оказва се, че без да зная, съм разрешил парадокс, свързан с Евклидовата специална относителност! Става дума за следното: "Because implies that photons travel at the speed of light in the subspace {x, y, z} and baryonic matter that is at rest in {x, y, z} travels normal to photons along , a paradox arises on how photons can be propagated in a space-time. The possible existence of parallel space-times or parallel worlds shifted and co-moving along is the approach of Giorgio Fontana. Euclidean geometry is consistent with Minkowski's classical theory of relativity. When the geometric projection of 4D properties to 3D space is made, the hyperbolic Minkowski geometry transforms into a rotation in 4D circular geometry." "Защото предполага, че фотоните се движат със скоростта на светлината в подпространството {x, y, z} и барионната материя, която е в покой в {x, y, z}, пътува нормално до фотони по протежение възниква парадокс за това как фотоните могат да се разпространяват в пространство-времето. Възможното съществуване на паралелни пространства-времена или паралелни светове се изместват и се движат заедно е подходът на Джорджо Фонтана. Евклидовата геометрия е в съответствие с класическата теория на относителността на Минковски. Когато се направи геометричната проекция на 4D свойствата в 3D пространството, хиперболичната геометрия на Минковски се трансформира във въртене в 4D кръгова геометрия." Какво означава това? Евклидовата специална относителност не само пресъздава подхода на Минковски посредством въртене между основната и примовите координатни системи по евклидов вместо по хиперболичен (при Минковски) кръг, с което няма никакви проблеми (всичко от диаграмите на Минковски се представя равностойно и от диаграмите на Епщайн, включително напълно се извеждат и Лоренцовите трансформации - Epstein Diagrams / Relativity ). Проблемният момент е, че Евклидовата специална относителност се опитва да използва и евклидово четириизмерно пространство, където състоянието на пространството по всички четири направления, включително и по w, е съвсем идентично (при Евклидовата специална относителност не само знаците пред стойностите на четирита компонента по диагонала на метричния тензор са еднакви, положителни, но и самите четири стойности също всички са еднакви, четири единици). Именно този опит да се ползва стандартно евклидово пространство, със стандартна, декартова координатна система, без никакви асиметрии, води и до гореспоменатия парадокс. Визуално парадоксът е изобразен в лявата част на следващото изображение: Вляво на изображението се вижда как когато пространствената протяжност по направлението на четвъртото пространствено измерение w се третира равностойно на останалите три направления (по измеренията х, у и z, като на изображението координата на z е игнорирана, за да може да се представи координата на w), излъчената от точка А светлина никога не може да достигне до точка В, понеже според тази концепция светлината се движи само по направленията х и у (и z, което не е дадено) и не се движи по направлението w, само по което пък се движат двете точки в покой една спрямо друга А и В. Докато излъчена в момента t1 светлина от точка А успее да достигне със скоростта се 1с точка В в момента t4, движейки се само по координатите х и у (и z), самите точки А и В ще са се преместили със същия темп 1с по координатата w (дадено в сиво и червено). По този начин излъчена където и да било в областта ху(z) светлина, която не може да се движи по w, понеже се движи с темп 1с изцяло в ху(z), ще остане в "миналото" и никога няма да достига и да бъде регистрирана от каквото и да било в настоящето. Това би трябвало да е парадокса, ако съм го разбрал правилно. При Динамичната Вселена обаче, където векторът на скоростта 1с на покоящи един спрямо друг обекти (тоест - движещи се заедно, със скорост 1с, само по направлението на координата w) съкращава лоренцово пространственото отстояние на Вселената по направлението w до планкова дължина, подобен парадокс практически НЯМА! Така светлината се движи с 1с само в обема ху(z) и понеже той е съкратен от гледна точка на покоящите обекти (заради движението им с 1с по w) - за тях светлината също може да се движи само в обема на това съкратено ху(z)-пространство (дясното изображение). Дори и обектите да се движат един спрямо друг с някаква подсветлинна скорост в обема ху(z) - светлината се движи с 1с в собственото 3D-пространсво ху(z) на всеки отделно дефиниран обект, с което се изпълнява постулата на Айнщайн за постоянството на скоростта на светлината във вакуум (че всеки наблюдател регистрира светлината със скорост 1с, независимо как той самия се движи или не спрямо останалите). Стойността на скоростта на светлината 1с е представена от същата стойност на вектора 1с на постоянно движение на материята в 4D-пространство. Всички постулати на Айнщайн, относителности, причинно-следствени връзки са изпълнени. До тук става дума за w-асиметрия (съкращаване на 4D-Вселената само по направлението на четвъртото пространствено измерение w, което състояние се променя единствено при задвижване между обектите в 3D-простанството), но броят на измеренията е четири и както може да има w-асиметрия, така би могло да има, паралелно, и х-, у- и z-асиметрии - възможност за съществуване на поне четири паралелни "свята", които не взаимодействат помежду си електромагнитно (потенциално обяснение на тъмната материя): [physics/0410054] The Four Space-times Model of Reality The Nature of Antimatter (dark matter) – Reading Feynman По тази причина най-вероятно ще продължа да ползвам определението за "Динамичната Вселена", но основното название ще бъда - Хипотеза за хиперизмерната асиметрия!