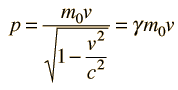gmladenov

Точно така. И след като масата не се променя, значи и скоростите не се променят. Ти нали знаеш колко е 2+2?

Именно. В случая си прав. Нютон е забелязал, че "така става на практика" - и оттам и закона. И тъй като живеем в същата реалност като Нютон, е напълно логично да очакваме запазване на импулса и в СТО. Просто така се получава на практика. Разликата между Нютон и СТО е, че колкото и да ускоряваш едно тяло, то не може да набере по-висока скорост от тази на светлината. Затова мъдрите релативисти са измислили концепцията за релативистката маса ... след което те пак мъдро са се отрекли от нея. И затова така и не е ясно защо в релативистката формула за импулса има и един (никому-ненужен) Лоренцов коефициент.

Ами точно затова е горният пример и както се вижда сумарната скорост на двете частици преди и след еластичния удар е една и съща във всяка от системите (въпреки че тя е различна между системите). Може да и не използвам правилната терминология, но казаното е вярно.

Колега, Айнщайн изрично указва в реферата си, че СТО се базира на "строгите стандарти на измерванията и методите на Евклидовата геометрия". Значи според самия Айнщайн ... цитиран дословно ... СТО е базирана на Евклидова геометрия. Ти обичаш да си фантазираш и според теб в нашата вселена има сума ти други измерения, но ако слушаме самият Айнщайн ... а не някой друг ... то СТО използва Евклидова геометрия. Ти разбираш ли концепцията за това да черпиш от извора, а не от други източници? Ако я разбираш, тогава ще трябва да приемеш, че СТО е базирана на Евклидова геометрия. Това е положението, Минке.

Запазването на импулса се приема за вярно по улсовие. Масата на частиците, дори да я смятаме по релативистки, не се променя "вътре" в една система. Значи във всяка система работим с една и съща маса преди и след еластичния удар - дори масата да има различна величина в различните системи. В горния пример цялостта на частиците се запазва преди и след удара, така че работим с една и съща маса. А от това пък следва, че запазването на импулса зависи единствено от запазване на скоростите преди и след удара. По силата на това, че запазването на импулса по улсовие се приема за вярно - и като се има предвид, че масата не се променя - то запазването на скоростите преди и след удара в същност е гарантирано в стационарната система. Въпросът е дали то е гарантирано и в примовата система след прилагане на Лоренцовата трансформация (ЛТ). Аз бях чел статии, според които ЛТ не гарантира запазване на скоростите в примовата система и тъй като не бях проверявал лично, го приемах за вярно. Но като се направят сметките в същност излиза, че ЛТ неизбежно запазва скоростите преди и след еластичен удар. ЛТ представлява криво огледало, но все пак огледало - и затова ако има запазване на скорости в стационарната система, то неизбежно ще има запазване на скорости и в примовата система (преди и след еластичен удар). Съотвено ми се изясни, че Лоренцовия фактор в релативистката формула за импулса не е свързан със скоростта, а с масата. Хубаво, но ако масата не се променя, то тогава Лоренцовият фактор не е свързан с нищо. Релативистите си го слагат за зор-заман.

Не си го уцелил. Задал съм улсовие на задачата, което ти не си прочел внимателни. От там почни.

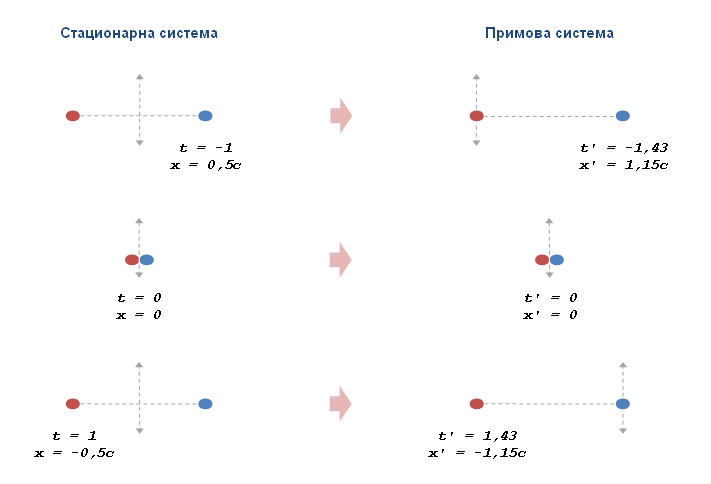
Запазване на импулса в СТО Следната картинка е илюстрация за запазването на импулса в стационарна и примова системи, както е според СТО. Имаме две частици с еднаква маса - червена и синя - които в стационрната система се движат със скорост 0,5с една към друга. В момент t=0 те се удрят еластично и сменят посоките си на 180° и започват да се отдалечават една от друга. Примовата система се движи в положителна посока със скорост v=0,5с спрямо стационарната система. Така червената частица е в покой в тази система до момента на удара ... след което тази частица започва да се движи, докато синята частица става покояща. Ето координатните сметки: v = 0.5c, γ = 1.15, x = 0.5c, t = -1 x' = γ(x - vt) = 1.15(0.5c + 0.5c) = 1.15c t' = γ(t - xv/cc) = 1.15(-1 - 0.5*0.5) = -1.43 v = 0.5c, γ = 1.15, x = -0.5c, t = 1 x' = γ(x - vt) = 1.15(-0.5c - 0.5c) = -1.15c t' = γ(t - xv/cc) = 1.15(1 + 0.5*0.5) = 1.43 На картинката ясно се вижда запазването на импулса след удара: в стционарната система двете частици имат еднакви скорости преди и след удара. В примовата система червената частица е в покой до удара, докато синята се движи със скорост 1,15с/-1,43 = -0,8с. След удара е обратното: синята частица е в покой, а червената се движи със скорост -0,8с. Ако приемем, че масата на частиците е еднаква и в двете системи, то тогава имаме запазване на класическия импулс. Така че няма никаква нужда да ползваме формулата за релавистичния импулс; това е излишно, след като класическия импулс се запазва. Формулата за релавистичния импулс има смисъл единствено ако масата на частиците се променя между двете системи; тоест, ако масата на частиците е релативистична. Тогава релативистичната формула ни дава импулса съгласно релативистичната маса на частиците. Но ако масата не се променя, релативистичната формула в същност е безсмислена и излишна.

Проблемът е, че формулата за релативистичния импулс има физически смисъл единствено ако имаме релативистична маса. Без такава маса няма обяснение защо Лоренцовия коефициент присъства във формулата. Аз направих няколко сметки и класическият импулс работи чудесно в СТО за хоризонтални еластични удари. Така че за тях релативистичната формула не е нужна. Не съм смятал, но е възможно е релативистичната формула за импулса да е нужна за вертикални еластични удари. Ако това е така, то релативистичната формула е просто "корегирана" версия на класоческата формула - необходима единствено за да излязат сметките. С други думи, релативисичната формула не е нищо друго освен шашма/стъкмистика, необходима за да излизат сметките.

Ще гледам да направя едни по-подробен пример, че нещо не ми излизат сметките. Апропо, Ричард Файнмън говори за релативистична маса в известните си лекции. Така че релативистичната маса не е просто объркване: https://www.feynmanlectures.caltech.edu/I_16.html

Така е, но разгледай следния пример: две топки за билярд се движат една към друга и се сблъскват. Първо използваш формулата за запазване на импусла в системата на масата за билярд, която приемаш за стационарна. След това пак смяташ импусла на топките в система на наблюдател, който се движи спрямо масата. Като сметнеш излиза, че имаш един и същи сумарен импулс и в двете системи: тази на масата и тази на подвижния наблюдател. Но ако направиш същите сметки по формулата на СТО, тогава сумарният импулс в двете системи няма да е еднакъв, а различен. За това става дума.

Става дума за импулса на движещи се тела в стационарна система - и импулсът на същите тези тела в подвижна/примова система. Например, подвижна топка за билярд в системата на маса за билярд - и същата топка в системата на кола, която се движи спрямо масата за билярд.

Да ... но в действителност се получава, че се ползват различни формули в стационарна и подвижна/примова системи. Класическата формула важи само в стационарни системи, докато в подвижни/примови не важи. Значи в крайна сметка за различните системи се ползват различни формули ... нищо че на пръв поглед излежда, че се ползваа една и съща формула.

Нека да се забелижи следното. Формулата за релативистичния импулс е: От формулата се вижда, че за (v=0) Лоренцовият коефициент е (γ=1), докато за (v>0) имаме (γ>1). А от това пък следва, че в стационарни системи, където (v=0), ползваме класическата формула за импулс (p=mv), докато в подвижни/примови системи ползваме релативистичната формула за импулс. С други думи, импулсът се смята по два различни начина в стационарни и подвижни системи. А щом това е така, значи имаме различен импулс в тези системи (иначе защо го смятаме по различен начин). Така в крайна сметка в СТО нямаме запазване на импулса между отправни системи. Имаме стъкмистика, според която законът за запазване на импулса се спазва ... но в действителност сумарният импулс в стационарна и подвижни системи е различен. Чрез стъкмистиката си, СТО върти двойно счетоводство за замазване на очите: уж имаме запазване на импулса между отправни системи, но в същност нямаме. Затова казваме, че СТО е математическа шашма.

Принципност по русоробски: Напълно нормално е да има руска асимилация в завладени с война територии ... но е престъпно и вероломно украинците (уж) да забраняват руския език в собствените си територи. Руснаците имат право да "разчистват" и завладяват територии ... но украинците са нацисти ако защитават собствените си територии.

За пореден път ще подчертая, че аз ти цитирам Айнщайн ... на което ти отговаряш, че аз си измислям. Там сме в споровете с теб.

Явно според теб е нормално да оставиш терористите да трепят, докато ти гледаш ... защото не си терорист. Не работят така нещата, колкото и да ти се иска. Парадоксът на насилието е, че насилие се побеждава с още по-голямо и по-вероломно насилие. Например, за да откажаш Хамас и Русия от бъдещи агресии, в идеалният случай трябва да ги заличиш от лицето на земята. За съжаление това не е реалистично и затова от тях могат да се очакват и бъдещи агресии. Но в крайна сметка ако искаш да решиш проблема един път завинаги, точно това трябва да се направи. Това е парадоксът на насилието: насилие се побеждава с по-голямо насилие. Бий, за да те уважават. Путин точно на този принцип действа.

Няма "днешно състояние" на СТО. Четем оригинала и от оттам черпим информация. Ако ти си измислиш, че според СТО има 17 измерения, теб ли слушаме ... или четем оригинала?

Да ... но е напълно уместно да се попита защо класическите формули не работят? Какво е обяснението за това. Разговорът тръгна от там, че релативистичният импулс е равен на класическият, умножен по Лоренцовия коефициент. И ако приемем, че масата се увеличава със скоростта, то това би имало физически смисъл. Само че ние казваме, че масата не се променя. Тогава е съвсем резонно да се попита защо е неободимо да уможим импулса по Лоренцовия коефициент ... и единственото "обяснение", което ти можеш да измъдриш, е че "такава е геометрията на пространство-времето". Хубаво, но това не е обяснение, а оправдание. Няма обяснение защо импулсът е пропорционален на Лоренцовия коефициент ... затова дай да го припишем на пространство-времето. Бабини деветини.

Хамас на какъв принцип взимат заложници?

Айнщайн не казвяа нищо подобно. Това, което Айнщайн казва, е че да се дефинира времето е трудно и затова вместо да дефинира времето, той ще приравни "време = показание на часовници". Минковкси, анализирайки СТО, достига до извода, че времето би могло да се разглежда като четвърто измерение. Но това е една чисто математическа интерпретация. Самият Айншщайн нищои подобно не казва.

Еее, ти пък сега. СТО не дефинира дали времето е човешка абстракция или физическо явление. Самият Айнщайн казва: за да избегнем трудностите, свързани с определението на "времето" ... Значи аз ти цитирам Айнщайн ... а ти ми твърдиш, че аз си измислям. Няма да се разберем.

Ествествено, че ми е ясно. Ти си този, който нещо се бърка. Ето ти запазване на импулса в стационарна и примова системи съгласно класическата физика: Стационарна система Примова система m1u1 + m2u2 = m1u3 + m2u4 m1u1' + m2u2' = m1u3' + m2u4' u' = (u - v) ⇒ (m1u1 - m1v) + (m2u2 - m2v) = (m1u3 - m1v) + (m2u4 - m2u4) ⇒ m1u1 + m2u2 = m1u3 + m2u4 Тук m1 и m2 са масите на две тела, които се се сблъскват в стационарната сисмета докато се движат със скорости u1 и u2. След сблъсъка масите на телата се запазват, докато скоростите им се променят на u3 и u4. В примовата система телата се движат със скорости u1' и u2' преди сблъсъка и u3' и u4' след сблъсъка. И както се вижда на таблицата, като заменим примовите скорости по формулата за класическо събиране на скорости, се получава запазване на импулса и в двете отправни системи. Ако направим същите сметки за примовите система - но вместо класическата формула за събиране на скорости излползваме формулата на СТО - тогава няма да се получи запазване на импулса. Затова казваме, че класическият импулс не се запазва в СТО. За да имаме запазване на импулса в СТО, трябва да ползваме релативистичната формула за импулс. Това е смисълът на тази формула: с класическата формула импулсът не се запазва, докато с релативистичната формула той се запазва.

Не спираш да ги ползваш, но приемаш, че те търпят критика по условие. И не обиждаш тези, които критикуват теориите и им намират маана.

Това е интерпретацията на Минковски, докато самата СТО не дефинира какво е време. Даже напротив, Айнщайн изрично избягва да дефинира какво е време: Может показаться, что все трудности, касающиеся определения «времени», могут быть преодолены тем, что вместо слова «время» я напишу «положение маленькой стрелки моих часов». Такое определение, действительно, достаточно в случае ... Това е цитат от трета страница на реферата: http://path-2.narod.ru/02/03/kedt.pdf. Айнщайн специално избягва дефиницията на време като заменя думата "време" с израза "положението на малките стрелки на моя часовник". С други думи, той приравнява "време = показание на часовник" и така хитро заобикаля дефиницията на време. Времето какво е: физическо явление или човешка абстракция? СТО не дава отговор на този въпрос - а той е важен, за да се разбере как подвижните часовници се забавят. Ако времето е абстракция (чети измислица), тогава как човешка измислица забавя часовници? Ако пък е физическо явление, то какво е? Материя, поле, сила, нещо друго? СТО не дава отговор.

"Засега няма нищо по-добро" не е аргумент, че дадена теория е добра/вярна. Представи си, че във вас влизат полицаи да те арестуват и ти казват: има убийство и засега нямаме по-добър заподозрян от теб. Затова ти ще лежиш в затвора. Ти ще се съгласиш ли с този аргумент? За СТО специално: СТО не дефинира какво е време, но приема за даденост, че подвижните часовници се забавят. Как, обаче, времето влияе на подвижните часовници? СТО не задава механизъм за това. Не става така. Това е съществен пропуск в теорията. Механизмът за забавяне на часовници трябва да бъде изяснен/зададен - и фактът е, че СТО не го задава. Съответно всяко обяснение в тази насока е само импровизация и преразказ с разсъждение. Тук не ни интересува какво е искал да каже Айнщайн, а какво е казал ... и той не е казал защо и как подвижните часовници се забавят. Така че ние в същност не знаем защо това е така; трябва да го приемем на юнашка вяра. Някои от нас, обаче, държат на доказателства и не приемат "истини" на юнашка вяра.