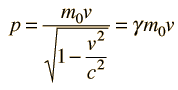gmladenov

Ние виждаме как се смята релативисткия импулс ... но се съгласяваме. И показваме с примери откъде идва несъгласието. А ти ни обясняваш, че релативисткия импулс се смята така, защото се смята така. Това е така, щото е така.

Ами точно това показва моя пример горе. В него всяка от двете частици се движи със скорост 0,5с в стационарната система. Така сумарната скорост в тази система е 1с. Но както се вижда, в примовата система сумарната скорост е 0,8с, а не 1с. Значи Лоренцовата трансфромация се справя с положението и намалява сумарната скорост, така че тя да не надвиши разрешеното.

Според мен нещо се бъркаш. Ограничението на СТО е, че нищо не може да се движи със скоростта на светлината. Но защо сумарната скорост на две или повече частици да не може да надвиши тази скорост?

Примерът е класически за запазване на импулса: еластичен удар на две частици/топки, при който сумата на скоростите преди и след удара се запазва ... след като по условие частиците имат еднаква маса. Горният пример показва, че Лоренцовата трансформация неизбежно запазва сумата на скоростите преди и след удара. Значи запазването на скоростите е вградено в ЛТ. Няма такъв филм, в който ЛТ не запазва сумата на скоростите. И след като сумата на скоростите се запазва по дефиниция, значи запазването на импулса зависи единствено от запазване на масата. Това целях да покажа: ЛТ запазва запазва сумата на скоростите (преди и след еластичен удар), така че запазването на импулса зависи от единствено от запазване на масата.

След като Хамас са почнали клането, не можеш да се оплакваш, че Израел отвръща. Ако Москва хвърли атомна бомба над Вашигнтон - както те редовно заплашват - гадните кравари ли са зверовете, ако те отвърнат на удара с атомна бомба над Москва? Като се знае каква реакция ще последнва след клане, не го почваш първи. Няма да разрешиш вековни/хилядолетни напрежения с клане - а само завъртиш цикъла наново.

В Близкия изток тече постоянен конфликт точно защото различните страни виждат "фактите" различно. Но със сигурност е факт, че с тероризъм нищо няма да се разреши. На интернета има видеа, които показват сегашните атаки на терористите. Можеш да видиш със собствените си очи как терористите, с калашници и пълна военна екипировка, нападат невинни и беззащитни хора. Има само една дума за подобно деяние: КЛАНЕ. Каквито и факти да изложиш, можеш да си напълно сигурен, че проблемите на Близкия изток няма да се решат с клането на невинни и беззащитни хора.

С всяко свое изказване Путин малко или много манипулира общественото мнение. И настина има достаъчно хора, които му вярват и искат да му вярват. Аз виждам на Дир.бг, например, как думите на Путин веднага стават про-руски опорки. Тези хора дефакто чакат някой като Путин да им говори как контраофанзивата се проваля, как Западът спира помощта си и т.н.. Контраофанзивата не е приключила, но се вижда колко бавно и трудно напредват украинците. И това естествено се използва за дезинформация и пропаганда. При всички случаи на Путин за нищо не може да се вярва, защото той е класически демагог и манипулатор. Неговите изказвания преследват други цели, а не да информират.

Има статии на интернета, според които законът за запазване не класическия импулс не работи в СТО. Обяснението е, че след трансформация на координати с Лоренцовата трансформация (ЛТ), скоростите в примовата система са такива, че класическия импулс не се запазва. По тази причина се налага използването на релативистката формула за импулс - а не класическата. Горният пример показва, обаче, че класическият импулс в същност се запазва след прилагане на ЛТ. Значи проблемът не е ЛТ, както се твърди в някои статии. Истинската причина за необходимостта от релативистки импулс е релативистката маса, която на теория се увеличава със скоростта. Тя е причината, заради която класическият импулс не се запазва в СТО. Хубаво, но според някои мъдри релативисти, като например Скенер, релативистката маса е отживелица. Добре, ние се съгласяваме с мъдрите релативисти - но в такъв случай релативистката формула за импулса става безсмислена, след като тя съществува единствено заради релативистката маса.

Виж сега, тази война ... както и всички злини по света ... са предизвикани от гадните кравари. Така че защо въобще си хабиш времето с някакви данни. Не е ли е ясно, че гадните и веролмнои кравари са организирали атаката на Хамас - само и само Израел да почне да избива невинни араби и така гадните кравари да печелят от войната и да заграбят безценните богатства на Русия и света.

Последно какво казват мъдрите релативисти: имаме ли релативистка маса или нямаме? Специално съм написал горе, че релативистката форула за имулса има смисъл само ако масата е релативистка. Доколкото знам, формулата за релатисткия импулс е изведена от Макс Планк - и ако той е вярвал, че масата е релативистка, тогава разбираме защо и формулата е такава, каквато е.

Какво "ами сега"? Нали точно това показва моят пример: В примовата система червената частица е стационарна (v=0), а синята е подвижна (v=0,8c). След еластичния удар, червената частица започва да се движи (v=0,8c), а синята частица става неподвижна (v=0).

Сто пъти поясних, че частиците в горния пример имат еднаква маса и запазват цялостта си - а оттам и масата си. Значи "вътре" във всяка една от системите масата не се променя (дори тя да се променя между системите). Оттук нататък масата може да се приеме за константа и така единственото нещо, от което зависи импулса, са скоростите на частиците. И както се вижда в примера, сумата от скорости също се запазва и в двете системи ... което е неизбежно, съгласно Лоренцовата трансфромация (ЛТ). Значи ЛТ е тази, която запазва скоростите и така Лоренцовия коефициент е напълни излишен във формулата за импулса (при положение, че масите не се променят). Този коефициент има евентуален смисъл само ако масите се променят ... но както мъдрите релативисти са решили, масата е константа. Така че самите мъдри релативисти са направили така, че Лоренцовия коефициент да е излишен.

Точно така. И след като масата не се променя, значи и скоростите не се променят. Ти нали знаеш колко е 2+2?

Именно. В случая си прав. Нютон е забелязал, че "така става на практика" - и оттам и закона. И тъй като живеем в същата реалност като Нютон, е напълно логично да очакваме запазване на импулса и в СТО. Просто така се получава на практика. Разликата между Нютон и СТО е, че колкото и да ускоряваш едно тяло, то не може да набере по-висока скорост от тази на светлината. Затова мъдрите релативисти са измислили концепцията за релативистката маса ... след което те пак мъдро са се отрекли от нея. И затова така и не е ясно защо в релативистката формула за импулса има и един (никому-ненужен) Лоренцов коефициент.

Ами точно затова е горният пример и както се вижда сумарната скорост на двете частици преди и след еластичния удар е една и съща във всяка от системите (въпреки че тя е различна между системите). Може да и не използвам правилната терминология, но казаното е вярно.

Колега, Айнщайн изрично указва в реферата си, че СТО се базира на "строгите стандарти на измерванията и методите на Евклидовата геометрия". Значи според самия Айнщайн ... цитиран дословно ... СТО е базирана на Евклидова геометрия. Ти обичаш да си фантазираш и според теб в нашата вселена има сума ти други измерения, но ако слушаме самият Айнщайн ... а не някой друг ... то СТО използва Евклидова геометрия. Ти разбираш ли концепцията за това да черпиш от извора, а не от други източници? Ако я разбираш, тогава ще трябва да приемеш, че СТО е базирана на Евклидова геометрия. Това е положението, Минке.

Запазването на импулса се приема за вярно по улсовие. Масата на частиците, дори да я смятаме по релативистки, не се променя "вътре" в една система. Значи във всяка система работим с една и съща маса преди и след еластичния удар - дори масата да има различна величина в различните системи. В горния пример цялостта на частиците се запазва преди и след удара, така че работим с една и съща маса. А от това пък следва, че запазването на импулса зависи единствено от запазване на скоростите преди и след удара. По силата на това, че запазването на импулса по улсовие се приема за вярно - и като се има предвид, че масата не се променя - то запазването на скоростите преди и след удара в същност е гарантирано в стационарната система. Въпросът е дали то е гарантирано и в примовата система след прилагане на Лоренцовата трансформация (ЛТ). Аз бях чел статии, според които ЛТ не гарантира запазване на скоростите в примовата система и тъй като не бях проверявал лично, го приемах за вярно. Но като се направят сметките в същност излиза, че ЛТ неизбежно запазва скоростите преди и след еластичен удар. ЛТ представлява криво огледало, но все пак огледало - и затова ако има запазване на скорости в стационарната система, то неизбежно ще има запазване на скорости и в примовата система (преди и след еластичен удар). Съотвено ми се изясни, че Лоренцовия фактор в релативистката формула за импулса не е свързан със скоростта, а с масата. Хубаво, но ако масата не се променя, то тогава Лоренцовият фактор не е свързан с нищо. Релативистите си го слагат за зор-заман.

Не си го уцелил. Задал съм улсовие на задачата, което ти не си прочел внимателни. От там почни.

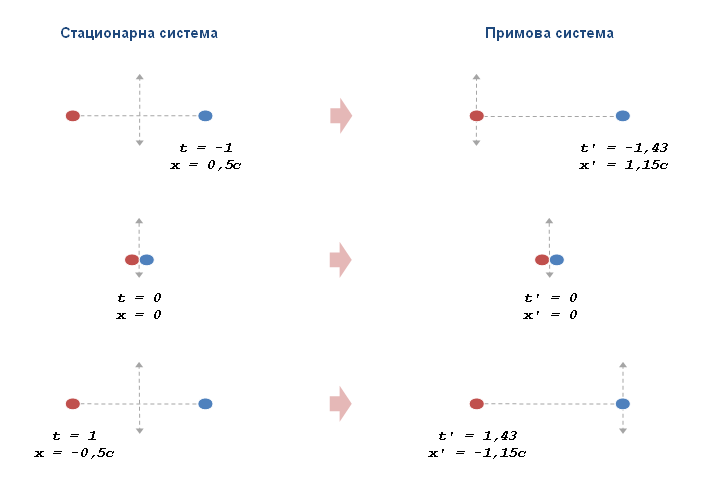
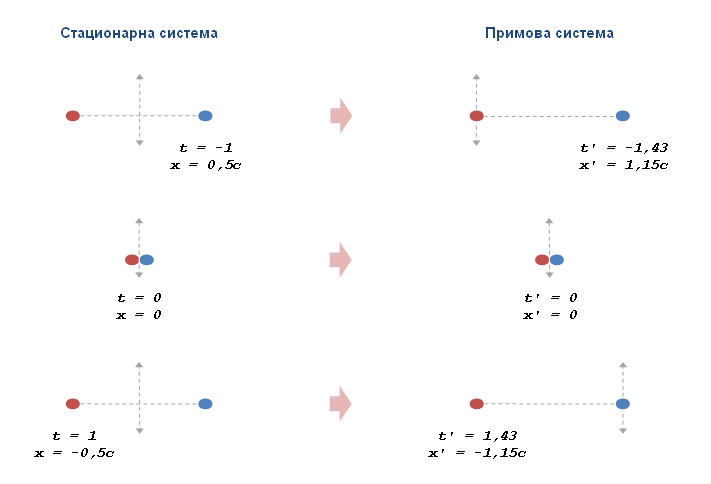
Запазване на импулса в СТО Следната картинка е илюстрация за запазването на импулса в стационарна и примова системи, както е според СТО. Имаме две частици с еднаква маса - червена и синя - които в стационрната система се движат със скорост 0,5с една към друга. В момент t=0 те се удрят еластично и сменят посоките си на 180° и започват да се отдалечават една от друга. Примовата система се движи в положителна посока със скорост v=0,5с спрямо стационарната система. Така червената частица е в покой в тази система до момента на удара ... след което тази частица започва да се движи, докато синята частица става покояща. Ето координатните сметки: v = 0.5c, γ = 1.15, x = 0.5c, t = -1 x' = γ(x - vt) = 1.15(0.5c + 0.5c) = 1.15c t' = γ(t - xv/cc) = 1.15(-1 - 0.5*0.5) = -1.43 v = 0.5c, γ = 1.15, x = -0.5c, t = 1 x' = γ(x - vt) = 1.15(-0.5c - 0.5c) = -1.15c t' = γ(t - xv/cc) = 1.15(1 + 0.5*0.5) = 1.43 На картинката ясно се вижда запазването на импулса след удара: в стционарната система двете частици имат еднакви скорости преди и след удара. В примовата система червената частица е в покой до удара, докато синята се движи със скорост 1,15с/-1,43 = -0,8с. След удара е обратното: синята частица е в покой, а червената се движи със скорост -0,8с. Ако приемем, че масата на частиците е еднаква и в двете системи, то тогава имаме запазване на класическия импулс. Така че няма никаква нужда да ползваме формулата за релавистичния импулс; това е излишно, след като класическия импулс се запазва. Формулата за релавистичния импулс има смисъл единствено ако масата на частиците се променя между двете системи; тоест, ако масата на частиците е релативистична. Тогава релативистичната формула ни дава импулса съгласно релативистичната маса на частиците. Но ако масата не се променя, релативистичната формула в същност е безсмислена и излишна.

Проблемът е, че формулата за релативистичния импулс има физически смисъл единствено ако имаме релативистична маса. Без такава маса няма обяснение защо Лоренцовия коефициент присъства във формулата. Аз направих няколко сметки и класическият импулс работи чудесно в СТО за хоризонтални еластични удари. Така че за тях релативистичната формула не е нужна. Не съм смятал, но е възможно е релативистичната формула за импулса да е нужна за вертикални еластични удари. Ако това е така, то релативистичната формула е просто "корегирана" версия на класоческата формула - необходима единствено за да излязат сметките. С други думи, релативисичната формула не е нищо друго освен шашма/стъкмистика, необходима за да излизат сметките.

Ще гледам да направя едни по-подробен пример, че нещо не ми излизат сметките. Апропо, Ричард Файнмън говори за релативистична маса в известните си лекции. Така че релативистичната маса не е просто объркване: https://www.feynmanlectures.caltech.edu/I_16.html

Така е, но разгледай следния пример: две топки за билярд се движат една към друга и се сблъскват. Първо използваш формулата за запазване на импусла в системата на масата за билярд, която приемаш за стационарна. След това пак смяташ импусла на топките в система на наблюдател, който се движи спрямо масата. Като сметнеш излиза, че имаш един и същи сумарен импулс и в двете системи: тази на масата и тази на подвижния наблюдател. Но ако направиш същите сметки по формулата на СТО, тогава сумарният импулс в двете системи няма да е еднакъв, а различен. За това става дума.

Става дума за импулса на движещи се тела в стационарна система - и импулсът на същите тези тела в подвижна/примова система. Например, подвижна топка за билярд в системата на маса за билярд - и същата топка в системата на кола, която се движи спрямо масата за билярд.

Да ... но в действителност се получава, че се ползват различни формули в стационарна и подвижна/примова системи. Класическата формула важи само в стационарни системи, докато в подвижни/примови не важи. Значи в крайна сметка за различните системи се ползват различни формули ... нищо че на пръв поглед излежда, че се ползваа една и съща формула.

Нека да се забелижи следното. Формулата за релативистичния импулс е: От формулата се вижда, че за (v=0) Лоренцовият коефициент е (γ=1), докато за (v>0) имаме (γ>1). А от това пък следва, че в стационарни системи, където (v=0), ползваме класическата формула за импулс (p=mv), докато в подвижни/примови системи ползваме релативистичната формула за импулс. С други думи, импулсът се смята по два различни начина в стационарни и подвижни системи. А щом това е така, значи имаме различен импулс в тези системи (иначе защо го смятаме по различен начин). Така в крайна сметка в СТО нямаме запазване на импулса между отправни системи. Имаме стъкмистика, според която законът за запазване на импулса се спазва ... но в действителност сумарният импулс в стационарна и подвижни системи е различен. Чрез стъкмистиката си, СТО върти двойно счетоводство за замазване на очите: уж имаме запазване на импулса между отправни системи, но в същност нямаме. Затова казваме, че СТО е математическа шашма.